1.3 Основные характеристики потоков вызовов.

1. Ведущая функция потока вызовов ();

2. Интенсивность потока вызовов ();

3. Параметр потока вызовов ().

Математическое ожидание числа вызовов, поступающих в интервале времени [0; t), называется ведущей функцией потока.

Обозначим эту функцию (0,t). Функция (0,t) – неотрицательная, неубывающая и в практических задачах принимает конечное значение.

Потоки с непрерывной ведущей функцией называются регулярными, а со ступенчатой – сингулярными. В дальнейшем будут рассматриваться только регулярные потоки.

Интенсивность потока является характеристикой стационарных потоков.

Под интенсивностью стационарного потока  понимают математическое ожидание числа вызовов, поступающих в единицу времени.

За единицу времени принимают среднее время обслуживания одного вызова.

Для нестационарных потоков существуют характеристики:

а) Средняя интенсивность потока за отрезок времени [a,b) - ;

б) Мгновенная интенсивность (t) .

Рис. 1.10 – К определению интенсивности потоков.

За время [0,a) поступает (0,a) вызовов;

За время [0,b) поступает (0,b) вызовов.

Тогда средняя интенсивность потока за отрезок [a,b) есть:

.

(0,а), (0,b) – математическое ожидание числа вызовов, поступающих в течение отрезков [0,а), [0,b).

(0,а), (0,b), (0,t) – ведущая функция потока.

Мгновенная интенсивность.

Рис. 1.11 – К определению мгновенной интенсивности потока вызовов.

За время [0,t) поступает (0,t) вызовов,

За время [0,t+) поступает (0,t+) вызовов.

Здесь (0,t), (0,t+) – ведущие функции потока

;

Мгновенная интенсивность – это производная ведущей функции потока.

Параметр потока

Под параметром потока  в момент времени t понимается предел отношения вероятности поступления 1-го и более вызовов за отрезок времени [t, t+] при  0 к этому промежутку времени при  0

Это плотность вероятности поступления вызовов в момент времени [t,t+].

Для стационарных потоков (t)=, т.е. не зависит от момента, к которому относится параметр.

Из определения следует

₁(t,t+)=(t)+0() при 0

В последнем 0()- бесконечно малая более высокого порядка чем 0

Тогда для стационарных потоков ₁(t,t+)=+0(), 0

Какова связь между  и ? (теорема Королюка - Зитека)

Для стационарных потоков (без док-ва)

.

Для стационарных ординарных потоков

=

Рис.1.11 - Иллюстрация теоремы Королюка-Зитека .

Пусть на первой оси стационарный ординарный поток с .₁ и ₁. В силу выше изложенного ₁=_1.

На второй оси показан неординарный поток, т.к. в каждый момент поступает 2 вызова

В каждый момент времени

₂=2₁=2₁

Моменты поступления вызовов зависят от  и определяются им, но  не зависит от того сколько вызовов поступит в момент времени.

1.4 Простейший поток вызовов.

На практике в качестве модели реальных потоков часто используют простейший поток вызовов.

Простейший поток вызовов - это ординарный, стационарный поток без последействия.

Математическая модель простейшего потока.

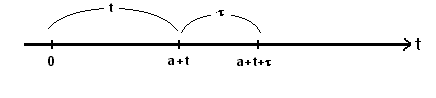
Рассмотрим отрезок времени и определим вероятность того, что в течение этого отрезка поступит ровноk вызовов,

т.е. Р_к(а,а+t+).

Представим этот отрезок времени двумя

[а,а+t) и [а+t,а+t+)

или [а,а+t+)=[а,а+t)+[а+t,а+t+)=[а,а+t)+[t,t+).

Таким образом, имеем

[а,а+t+)=[а,а+t)+[t,t+).

За это время согласно условию должно поступить k вызовов.

Возможны следующие случаи:

За I отрезок поступит За II отрезок

1.k вызовов 0 вызовов

2. k-1 1

3. k-2 2

………………………………………………….

.…………………………………………………

………………………………………………….

k-i i

…………………………………………………..

0 k

Введем обозначения :

Р_к-i(а,а+t)- вероятность поступления k-i вызовов за отрезок времени [а,а+t),

Р_i(t,t+)- вероятность поступления i вызовов за время [t,t+).

Тогда искомую вероятность можно найти, как произведение вероятностей

т.к. поток простейший, т.е. без последействия и, следовательно, поступление k-i вызовов и i вызовов- события независимы. Устремим 0.

Тогда в силу ординарности потока за 0 может поступить только 1 либо 0 вызовов. Откуда

.

Здесь 0() учитывает вероятность поступления 2 и более вызовов за 0.

Вместо i поставим его значение

Р_k(а,а+t+)=Р_k-1(а,а+t)P₁(t,t+)+Р_k(а,а+t)Р₀(t,t+)+0() при 0, k=0,1,2…..

Напомним, что k число за промежуток [а,а+t+). Вероятность того, что за [t,t+) поступит только один вызов

Р₁(t,t+)=₁(t,t+)-₂(t,t+).

Из определения параметра потока

₁(t,t+)=+0₁(), 0

В силу ординарности потока

₂(t,t+)=0₂()

Перед бесконечно малыми величинами всегда ставим знак плюс, т.к. вероятность не может быть отрицательной.

Тогда

Р₁(t,t+)=+0₁()

Р₀(t,t+)=₀(t,t+)-₁(t,t+)=1-t+0₂() при 0.

Здесь Р₀(t,t+)- вероятность поступления точно нуля вызовов за время [t,t+), а вероятность поступления 0,1,2… вызова за [t,t+]

₀(t,t+)=1, т.е. явл. достоверное.

Индексы 1,2….. в 0() указывает на различия между бесконечно малыми величинами.

Таким образом,

Р_k(а,а+t+)=P_k-1(а,а+t)[+0 ₁()]+Р_k(а,а+t)[1-+0 ₂()]+0₃() при 0 k=0,1,2…

Перенесем из правой части в левую Р_k(а,а+t) и поделим обе части на 

;

0, k=0,1,2…

устремим пределу обе части уравнения

, т.к.

.

Получим

при k=0,1…,.

Итак, имеем систему дифференциальных уравнений, которые будем решать методом производящих функций, который является основным методом комбинаторного анализа.

Идея метода заключается в следующем:

Есть последовательность

а₀,а₁,……………., а_к…

Производящей функцией этой последовательности является сумма ряда

Если известно, что последняя сумма сходится в окрестности точки х=0, то ищется ряд А(х).Далее, имея ввиду однозначное соответствие между членами обоих рядов, нетрудно найти все члены первой последовательности.

В нашем случае имеем

при k=0,1,2…

Суммируя обе части уравнения

.

Сумма производных равна производной суммы (свойства аддитивности производной).

.

обозначим

- производящая функция, зависящая от t и х,

а выражение

т.к. при k=0 это выражение смысла не имеет (Р_-1).

Обозначим k-1=n,

если k=1, то n=0,

если k=, то n=

Перейдя к новой переменной суммирования

вместо n напишем снова k

Интегрируем обе части от 0 до t

т.к. t=0.

В силу ординарности потока

следовательно при k=2,3…

или

,

т.к.

вместо Ф(t,x) подставим его значение.

В результате получаем формулу Пуассона, которая определяет вероятность того, что на интервале времени (t) поступит точно (k) вызовов.

.

Принимая t=1:

.

Графическая иллюстрация:

Рис. 1.12 – Завмсимость P_k=f(k).

Из рисунка видно, что при увеличении  форма огибающей закона Пуассона приближается к нормальному закону распределения. При >10 они практически сливаются.

Покажем, что формула Пуассона является законом распределения СВ (k).

.

Таким образом, формула Пуассона обладает основным свойством любого закона распределения.

Можно показать, что сумма независимых простейших потоков образует также простейший поток с параметром, равным сумме параметров объединяемых потоков.

Для распределения Пуассона справедливы следующие соотношения:

При t=1:

.