5.3. Идеально - симметричное неполнодоступное включение

Эрлангом предложен метод расчета пропускной способности неполно­доступных схем с учетом их микросостояний для идеального симметричного включения.

Идеально – симметричное включение – это такое неполнодоступное включение пучка емкостью  линий в g равновероятно занимаемых нагрузоч­ных групп с доступностью d каждая, в котором число нагрузочных групп и каждая линия пучка включается в выходы различных сочетаний нагрузочных групп.

Получаем абсолютно симметричную схему. Это позволит исследовать только ее микросостояния. Эта схема является равномерным включением, т.к. имеет место равновероятное занятие выходов.

Почему она называется идеальной?

число очень большое.

Реально такие числа, т.е. количество нагрузочных групп не имеет место.

Схема предложена для определения пропускной способности неполно­доступных схем.

V =5, d=3.

Составим таблицу различных состояний:

N,N нагрузоч­ной группы	1	2	3	4	5	6	7	8	9	10
Номера линий	1,2,3	1,2,4	1,2,5	1,3,4	1,3,5	1,4,5	2,3,4	2,3,5	2,4,5	3,4,5

Составим схему идеально – симметричного включения:

Такие схемы являются симметричными, т.к. каждую нагрузочную группу равновероятно обслуживает d линий из V. Благодаря этому, а также тому, что каждая нагрузочная группа обслуживается сочетанием выходов. Например, 1^я группа 1,2,3 выход и это сочетание не повторяется у других групп. Сочетание выходов для двух направлений групп отличается как минимум на единицу. Бла­годаря этим свойствам каждый выход из V линий пропускает одинаковую на­грузку. Поэтому можно обойтись рассмотрением лишь макросостояний, не затрагивая микросостояний коммутационной системы.

При входящем потоке вызовов – простейшем – его параметр не зависит от состояния коммутационной системы. Следовательно, с точки зрения потока можно не учитывать микросостояний коммутационной системы.

Пропускная способность идеального включения дает хорошее приближе­ние для реальных равномерных неполнодоступных схем и менее точную для ступенчатых неполнодоступных схем.

Эти схемы имеют большое число нагрузочных групп. Уже при пучке V=10 линий и d = 4 оказывается . На практике такое число нагрузочных групп не применяется.

5.4. Обслуживание простейшего потока вызовов идеально – симметричным пучком линий. Схема с потерями.

Пусть на схему идеально – симметричного включения, в которую включен пучок линий емкостью V линий, поступает простейший поток вызовов с параметрами λ. Закон распределения длительности обслуживания вызовов зкспоненциальный:

здесь Т – длительность обслуживания.

Необходимо найти:

Р_i – вероятность того, что в любой момент времени в системе занято i линий, т.е. система находится в i^ом состоянии.

Р_в – потери по вызовам.

Обозначения:

i – состояние КС, т.е. точное число линий, занятых в КС в рассматриваемый момент времени.

_i – вероятность того, что вызов, поступивший в КС, находящуюся в iом состоянии, будет обслужен (условная вероятность).

Структура идеально – симметричного включения:

если i < d, то φi = 1. Все вызовы обслуживаются.

если d ≤ i ≤ V - 1, то 0 < φ < 1.

i = V, то φ_i = 0. Все линии пучка заняты и вызов теряется.

Рассмотрим систему в моменты времени t и t+и посмотрим, как изменится ее состояние запри0

Нам нужно определить вероятность того, что в момент времени (t + ) система находится в состоянии i, при условии, что в момент t она находилась в любом состоянии.

Причем в момент времени t нас интересует состояние, когда заняты i-1, i, i+1 линии. Если в t было состояние i-2, i+2 и т.д., но вероятность перехода из таких состояний в требуемое есть величина бесконечно малая, боле высокого порядка малости чем   0.

t		За ()	(t +)	Вероятности переходов
Рi-1(t)	i-1	1 вызов	i	i-1 Pв()
Рi(t)	I	1 вызов, 1 осв.	i	[1 – Pв()φi - Pосв()]
Рi+1(t)	i+1	1 осв.	i	Pосв()

Если в момент времени t система была в состоянии i-1 и за  поступит 1 вызов, то система не обязательно перейдет в состояние i, т.к. система неполнодоступная. Здесь необходимо учитывать величину φ_i – условную вероятность того, что вызов, поступивший в состоянии i будет обслужен.

По общей методике, которая неоднократно излагалась ранее, составляется система уравнений:

Pi(t+)1 = Pi-1(t)Pв()φi-1,  0

Pi(t+)2 = Pi(t)[1 - Pв()φi – Pосв()],  0

Pi(t+)3 = Pi+1(t)Pосв(),  0

Pi(t+)4 = 0(),  0

P_осв() умножать на φ не нужно, т.к. процесс освобождения не зависит от структуры пучка.

P_i(t+)₄ – учитывает вероятность всех остальных состояний.

Тогда вероятность того, что в момент времени (t+) система находится в состоянии ' i ' равна:

пусть i = 0 в момент t:

при i=1  v-1

при i = v

Нам необходимо определить:

Р_в() - ?, Р_осв(), φ_i - ?

Учитывая, что входящий поток является простейшим

Р_в()=λ + 0₁(); Р_осв()=i + 0₂() и, что φ_i*0()=0(),

подставим полученные результаты в систему уравнений:

итак, имеем систему уравнений.

Перепишем из правых частей в левые P_i(t), P_v(t), разделим все на  и возьмем пределы их отношений при  0.

В левых частях получим

а Р_i(t)=P_i в следствии стационарности потока. Аналогичные результаты будут и при i = 0 и i = V. Кроме того, пределы:

тогда уравнения приобретают следующий вид:

всего имеем v+1 уравнение.

Из первого:

i = 0	P1=λР0φ0
i = 1
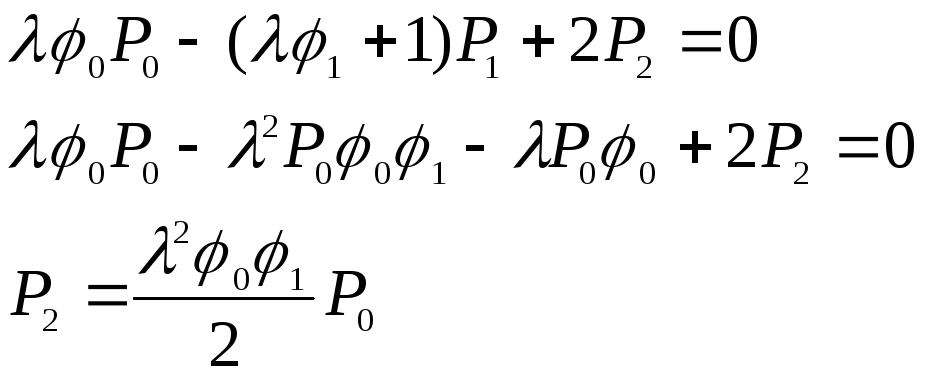
i = 2

Аналогично

выдвигаем гипотезу, что

правильность этой гипотезы проверим для последнего уравнения

i = v

следовательно наше предположение верно

Р₀, как и прежде найдем из условия нормировки

откуда

изменим, во избежании путаницы, индекс в знаменателе

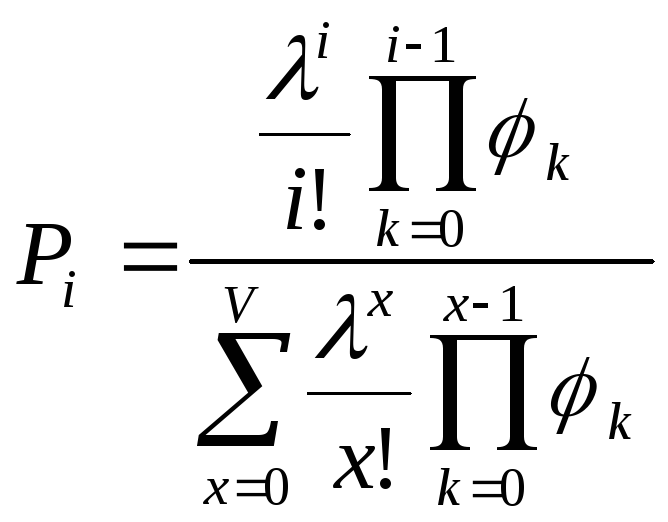
Осталась неизвестной величина φ.

Введем еще одну величину:

Ψ_i – условная вероятность того, что в момент поступления вызова система находится в состоянии i, то вызов будет потерян, т.е.

φ_i + Ψ_i = 1 или φ_i = 1 - Ψ_i, или Ψ_i = 1 - φ_i

Ψ_i – определяем из классического определения вероятности, как отношение благоприятных элементарных состояний ко всем возможным состояниям.

Имеется пучок емкостью V. Из этого числа занято точно i линий. Таких сочетаний всего может быть . Поступивший вызов будет потерян в том случае, если среди i занятых линий находится d фиксированных линий. Число таких состояний определяется числом сочетаний изV - d по i – d.

.

Тогда:

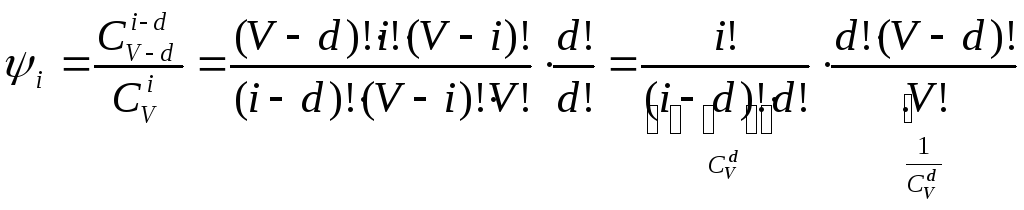
итак:

Тогда

Первые d множетелей равны единице, т.к. для i < d вызов, поступивший в систему, будет обслужен с вероятностью, равной единице.

Т.е.

Тогда

Согласно задания необходимо найти Р_в – потери по вызовам.

,

где:

_п – интенсивность потерянного потока вызовов,

 - интенсивность поступающего потока вызовов.

Для простейшего потока вызовов  = λ или учитывая, что  есть математическое ожидание числа вызовов

Тогда

Или

Для простейшего потока вызовов в случае экспоненциального времени обслуживания Н(х)=1 – е^-х при  = 1 Y = λ.

Тогда:

,

.

Эти выражения получили название третьей формулы Эрланга.

Р_i – вероятность занятости в неполнодоступной КС ровно i линий при простейшем потоке на входе.

Эти формулы можно использовать при расчете равномерных неполнодоступных схем и с меньшим приближением для расчета пропускной способности ступенчатых схем.