4.3 Функция распределения времени ожидания начала обслуживания. Экспоненциальное распределение длительности обслуживания вызовов.

В системах с ожиданием важно знать, сколько абонент будет ждать начала обслуживания. Здесь необходимо кроме P_t и Р_в найти t_ож (время ожидания начала обслуживания). В теории телетрафика t_ож характеризуют в вероятностном смысле следующей величиной:

P(t_ож<c) –

-это вероятность того, что время ожидания меньше какой-то «с». При этом, чем больше P(t_ож<c), тем лучше качество обслуживания и, наоборот, P(t_ож>c), тем хуже качество обслуживания.

Оценку лучше делать применительно к относительным величинам. За относительную единицу принимают среднее время обслуживания одного вызова (математическое ожидание) – МТ.

,

где:  - время ожидания начала обслуживания одного вызова в условных единицах.

Найдем допустимое время ожидания начала обслуживания в относительных единицах.

,

где: с – допустимое время начала обслуживания в абсолютных единицах.

Какова же вероятность Р(>t) при t=t₁,t₂,t₃ ?

Задача. На полнодоступный пучок линий емкостью v поступает простейший поток вызовов, создающий нагрузку у. Закон распределения длительности обслуживания экспоненциальный.

.

Пусть =y<v. Вызовы, находящиеся на ожидании обслуживаются в порядке очереди.

Требуется определить Р(>t), т.е. вероятность того, что время до начала обслуживания превысит t.

Введем следующие обозначения:

1. k – состояние коммутационной системы. Общее число вызовов на обслуживание и ожидание. Если i=0v-1, то k=i. Если заняты все v линий пучка и j=0,1,… , то k=v+j.

2. P_k(>t) – вероятность того, что вызов, поступивший в момент k-го состояния КС будет ждать начала обслуживания время, большее t.

3. Р_k – вероятность того, что система находится в k-ом состоянии (k=v+j).

Тогда

и есть вероятность того, что длительность ожидания начала обслуживания превысит

.

При k=v+j очевидно следующее равенство:

P_k=W_j .

Тогда j=k-v и, следовательно, P_k=W_k-v. Величину W_k-v мы определили раньше. Тогда

.

Итак, в системе находится k вызовов всего, а на ожидании находится k-v вызовов. Положим, поступает k+1 вызов. Тогда он будет по очереди (k-v+1)-ым. Если за время t поступает k-v+1 вызов и все будут обслужены, то, очевидно, что выражение будет неправильным (время ожидания начала обслуживания ни у одного вызова не превысило t).

Чтобы это неравенство (>t) было справедливо, необходимо, чтобы за время t было обслужено не более (k-v) вызовов. Тогда для k-v+1 вызова будет справедливым (>t).

Для этого необходимо, чтобы за время t было 1, 2, 3,…, k-v-2, k-v-1, k-v освобождений. Другими словами поток освобождений должен быть не более k-v. По условию, закон распределения длительности обслуживания экспоненциальный:

.

Здесь Т – время обслуживания. Нас же интересует величина t в неравенстве >t. В предыдущее выражение вместо (х) подставим (t):

или —

— это вероятность того, что длительность обслуживания превысит t. Эта величина для всех v линий равна:

Тогда вероятность того, что хотя бы один из вызовов будет обслужен за время (T<t) будет равна:

является характеристикой потока освобождений.

Функция распределения промежутков между вызовами для простейшего потока F(t) равна:

.

Итак, поток освобождений есть простейший поток с параметром

=v.

Для простейшего потока вероятность поступления за t равно i вызовов или i освобождений определяется формулой Пуассона:

,

при =v: .

Тогда вероятность того, что за время t произойдет не более k-v освобождений есть сумма:

.

А это, как было показано выше, и есть вероятность P_k(>t):

.

Подставляем выражения для P_k и P_k(>t) в искомую формулу:

Рассмотрим эти выражения и упростим их.

1.

С учетом этих преобразований:

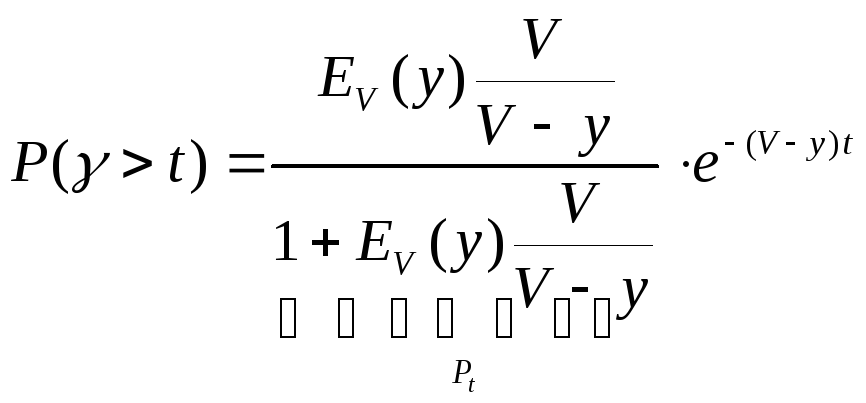
или.

Таким образом, P(>t)=f(t,y,v). Для разных t эта формула табулирована.

Системы с ожиданием характеризует более обще, чем , ее средняя величина. Таким образом, - среднее время ожидания начала обслуживания (математическое ожидание начала обслуживания).

.

Для непрерывной с.в., какой является время:

.

Зная Р_t легко находится среднее время ожидания начала обслуживания. Р_t – табулирована. Кроме этой величины очень важно знать среднее число вызовов, находящихся на ожидании - . Аналогично с-- это математическое ожидании.

Найдем сумму :

Тогда:

,

Но

.

Тогда

или .

P_v – табулирована. Поэтому, зная ее, всегда можно найти и .

Итак, задача решена. Мы получили закономерности:

P(>t) – вероятность того, что длительность ожидания начала обслуживания превысит t;

- среднее время ожидания начала обслуживания;

- среднюю длину очереди.

Выражения для ,иj, полученные выше есть функции от t, y, v, т.е

.

Проиллюстрируем эти выражения на следующих графиках.

при v=v₁, v₂, v₃,. причем v_1>v₂> v₃. Из графиков видно, что чем больше заданное время ожидания начала обслуживания, тем меньше вероятность .

Рис. 4.4 – Зависимость приv=v₁, v₂, v₃.

Чем больше v, тем меньше, т.е. тем лучше качество обслуживания при заданномt. При фиксированном t=t₁:

.

, v=v₁, æ= æ₁, æ₂, æ₃ (пропускная способность).

æ₁< æ₂< æ₃.

При одной и той же емкости пучка с увеличением удельной пропускной способности увеличивается, т.е. ухудшается качество обслуживания.

Рис. 4.5 – Зависимость при æ= æ₁, æ₂, æ₃.

=f(æ), v=v₁, v₂, v₃.

v₁<v₂<v₃.

Увеличение v при æ= æ₁ уменьшает среднее время ожидания начала обслуживания, т.е. качество обслуживания повышается.

Рис. 4.6 – Зависимость =f(æ) при v=v₁, v₂, v₃.