Тема 4 полнодоступный пучок. Система с ожиданием.

4.1 Постановка задачи.

Под системой с ожиданием понимается такая дисциплина обслуживания поступающего потока вызовов, когда поступивший вызов при занятости соединительных путей, способных его обслужить, не теряется, а становится в очередь и обслуживается с ожиданием.

Пусть имеется КС из v линий. При числе занятых линий поступающий поток вызовов обслуживается без ожидания. Когдаi=v, то поступивший вызов становится в очередь и обслуживается с ожиданием.

Таким образом, при iv-1 система с ожиданием не отличается от системы с потерями. При i=v вновь поступившие вызовы станут на ожидание, т.е. будут условно потеряны. Обозначим через «j» число вызовов, стоящих на ожидании.

Пример: Пусть входящий поток вызовов примитивный. Тогда j_макс=k-v – максимальная длина очереди. В случае простейшего потока «k» неограниченно и поэтому j=0, 1, ... , .

КС полнодоступная, поэтому любой вход доступен любому выходу. Следовательно, не нужно заниматься исследованием микросостояний КС, а достаточно ограничиться исследованием макросостояний (общее число занятых источников, а не их номера).

Для простейшего потока ^s= не зависит от состояния КС. Под состоянием КС будем понимать число занятых линий, а если заняты все, то число вызовов, находящихся на ожидании:

i – число занятых линий;

j – число вызовов на ожидании.

Здесь могут быть следующие случаи:

• В пучке занято точно i линий и i<v (i=0, 1, 2, ... ,v-1), то k=i. Число занятых линий при i<v однозначно определяет состояние КС. В этом случае может быть всего v состояний.

• i=v и на ожидании j=0, 1, 2, ... вызовов, то k=v+j. В этом случае может быть  число состояний. Таким образом, число макросостояний равно .

В системах с потерями на величину нагрузки не накладывается никаких ограничений. При этом, чем больше нагрузка, тем больше были потери. В системах с ожиданием все вызовы должны быть обслужены. Поэтому во избежании очереди, равной  на величину входящей нагрузки необходимо ввести ограничения. Какие? Допустим, что y<v. Каждая линия может обслужить максимально 1 Эрланг, следовательно, v линий – v Эрланг. При y=v все линии будут непрерывно заняты, а при y>v очередь будет стремиться к ; из-за неравномерности поступающих вызовов и при y=v длина очереди тоже будет стремиться к .

Таким образом, обязательное условие:

y<v –

- вообще, а для простейшего потока вызовов: у=<v.

4.2 Обслуживание однозвенной полнодоступной коммутационной системой простейшего потока вызовов. Система с ожиданием. Модель типа m/m/V. Вторая формула Эрланга

Имеется полнодоступная однозвенная коммутационная система с пучком емкостью v линий. На эту систему поступает простейший поток вызовов с параметром . Закон распределения длительности обслуживания экспоненциальный :

H(x)=P(T<x)=1-e^-x.

Принимаем, как и раньше, что постоянная обслуживания =1.

Какова вероятность того, что в системе занято точно i линий. P_i=?

Какова вероятность того, что на ожидании находятся ровно j вызовов. W_j=?

Кроме этого P_t=?, P_в=?

Все это при ограничении <v.

Нас интересует в любой произвольный момент времени P_i(t), W_j(t). Рассмотрим вначале не момент времени t, а момент времени [t+).

Все дальнейшие рассуждения будут проводиться при условии, что 0. вероятности P_i и W_j определяются состоянием коммутационной системы.

Каковы эти состояния?

Момент времени t	За 
i-1	1 выз.
i	-
i +1	1осв.
j-1	1 выз.
j	-
j+1	1 осв.

Остальные состояния имеют место с вероятностью о().

Пока система находится в состоянии V=1, то обслуживание с ожиданием не отличается от обслуживания с потерями. Поэтому первые V-1 уравнений будут такими же как и раньше, т.е.

i=0: P₀(t+)=P₀(t)[1-P_в()]+P₁(t)P_осв()+o();

в общем виде: P_i(t+)=P_i-1(t)[P_в()]+P_i(t)[1-P_в()-P_осв()]+ P_i+1(t)P_осв()+o(), 0.

i=v: при i=v, j=0, 1, 2, ... , .

Обозначим через P_v(t+) – вероятность того, что в системе занято v линий и на ожидании находятся 0 вызовов. Тогда P_v(t)=W₀(t) и

P_v(t+)=W₀(t+)=P_v-1(t)P_в()+P_v(t)[1-P_в()-P_осв()]+ +W₁(t)P_осв()+o(), 0.

Здесь W₁(t) – вероятность того, что на ожидании находится один вызов.

W_j(t+) - ? при i=v

W_j(t+)=W_j-1(t)P_в()+W_j(t)[1-P_в()-P_осв()]+W_j+1(t)P_осв()+o(), j=0, 1, 2, ... , ; 0.

При j=0 справедливо предыдущее уравнение.

Итак, мы имеем систему бесконечного числа уравнений. Неизвестно P_в()-? P_осв() - ? Эти величины не зависят от дисциплины обслуживания, т.к. являются атрибутами потока вызовов. Поэтому можно воспользоваться ранее полученными выражениями:

P_в()=_i+o(), P_осв()=i+o()

или при _i=:

P_в()=+o(), P_осв()=i+o().

i<v: P_осв()=i+o();

i=v; j=0, 1, 2, ... , : P_осв()=v+o() при любом j;

P₀(t+)=P₀(t)[1-t+o₁()]+P₁(t)[+o₂()]+o₃(), 0;

P_i(t+)=P_i-1(t)[+o₁()]+P_i(t)[1-+o₂()-i+o₃()]+ +P_i+1(t)[(i+1)+o₄()]+o₅(), 0, i=1, 2, ... , v-1;

P_v(t+)=P_v-1(t)[+o₁()]+P_v(t)[1-+o₂()-v+o₃()]+o₄()+W₁(t)[v+o₅()];

W_j(t+)=W_j-1(t)[+o₁()]+W_j(t)1[1-+o₁()-v+o₂()]+ +W_j+1(t)[v+o₃()]+o₄(), j=0, 1, 2, ... , ; 0.

Перенесем в левые части из правых P₀(t), P_i(t), W_j(t) и возьмем предел предварительно поделив все на 0.

Тогда

Производные по t равны нулю, т.к. поток стационарен и P_i(t)=P_i и W_j(t)=W_j.

В правой части все отношения в пределе равны нулю:

.

С учетом вышеизложенных замечаний получим систему:

i=0: -P₀+P₁=0;

i=1, ..., v-1: P_i-1-(+i)P_i+P_i+1(i+1)=0;

i=v, j=0: P_v-1-(+v)P_v+vW₁=0;

i=v, j=1, ... , : W_j-1-(+v)W_j+vW_j+1=0.

Выразим P_i и W_j через P₀:

i=0: Р1=Р₀;

i=1: P₀-(+1)P₁+2P₂=0;

P₀-(+1)P_o+2P₂=0;

²P₀=2P₂;

;

i=2: P_i-(+2)P₂+3P₃=0;

;

;

.

С помощью метода индукции можно предположить, что эта закономерность верна для других i, т.е.

Проверим правильность этого утверждения для i=v.

v-1=i:

P_v-2-(+v-1)P_v-1+vP_v=0;

;

После упрощений:

;

что и требовалось доказать. Таким образом:

, i=1, ... ,V-1;

.

Подставим эти выражения в уравнение для j=0.

j=0:

,

откуда:

.

j=1: Последнее уравнение системы:

,

откуда:

,

.

Предположим, что этот закон справедлив для любого j:

.

Проверим справедливость гипотезы для W_j+1:

,

,

что и требовалось доказать.

Найдем Р₀ из следующего условия:

, (I)

уравнение (I) можно записать иначе:

. (II)

Решим уравнение (I):

;

.

Распишем вторую сумму в знаменателе:

.

<v – ограничение, введенное при постановке задачи. Это бесконечно убывающая геометрическая прогрессия, ее сумма равна:

при q<1,

где .

Для второго уравнения:

.

Таким образом, для уравнения (I):

,

Для уравнения (II):

Подставим полученные выражения для P_i и W_j, а в знаменателе во избежание путаницы сменим переменные суммирования:

,

.

Для простейшего потока вызовов =у. Тогда:

.

Для простейшего потока было получено:

,

а .

В выражении для P_i в системе с ожиданием произведем некоторые преобразования:

.

Таким образом, для системы с ожиданием:

.

Сравним P_i(П) и P_i(O),

где: P_i(П) – для систем с потерями,

P_i(O) – для систем с ожиданием.

В выражении для P_i(O) знаменатель больше 1. Следовательно:

Р_i(О)<Р_i(П).

Это в свою очередь означает:

А это значит, что

.

Доля времени, в течение которой нет потерь, в системе с потерями больше, чем доля времени в системе с ожиданием.

Рекуррентная формула.

.

Для i-1 : .

Найдем отношение.

,

.

Найдем рекуррентное соотношение.

;

или

По условию y<v, поэтому , следовательно,

W_j < W_j-1 < W_j-2 < ... илиW₀>W₁>W₂.

Определим потери по времени – P_t.

P_t – это доля времени, когда заняты все линии пучка и на ожидании может находиться j=0, 1, 2, ... ,  вызовов.

.

Здесь сумма геометрической прогрессии .

.

Итак,

.

Сравним P_t(П) и P_t(O). Знаменатель у P_t(O)<1, следовательно:

P_t(O)>P_t(П).

Потери по времени в системах с ожиданием больше потерь по времени в системах с потерями.

Найдем потери по вызовам.

.

В системах с ожиданием под потерями по вызовам понимается доля времени, в течение которой на ожидании находится хотя бы один вызов.

.

.

.

Сравним Р_в(О) и Р_в(П).

, где - какое-то положительное число.

1-Е_v(у) – число также положительное.

Если , то знаменатель > 1.

Р_в(О)<Р_в(П)

Если , то

Р_в(О) Р_в(П)

Сравним для системы с ожиданием Р_t и Р_в.

; .

, т.к. y<v, то , т.е.

Р_t>P_в.

Найдем Р_v:

,

,

откуда:

.

Итак, мы получили: P_i, W_j, P_t, P_в  f(y,v). Это вторая формула Эрланга. P_t – табулирована. Зная P_t можно найти P_v и Р_в. Проиллюстрируем полученные выражения графически.

y=f(v), при P=P₁, P₂.

При Р₁, v₁: y₁>y₂ , т.к. в системе с потерями пропускается большая нагрузка.

При у₁ в системе с «П» нужно v₁ линий, а в системе с ожиданием нужно v₂ линий.

v₂>v₁.

Пример: y=40 Эрл. и р=0,005:

v₁(П)=56 линий, v₂=60 линий.

Пропускная способность систем с потерями выше пропускной способности систем с ожиданием.

æ=f(v), при P=P₁, P₂.

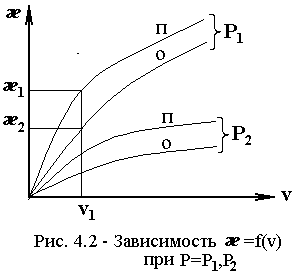
При v=v₁: æ₁>æ₂.

=f(P), при v=v₁.

Вобласти малых потерь пропускная способность каждой линии пучка в системе с потерями выше, чем в системе с ожиданием. С увеличением потерь это отличие уменьшается.

Пример.

=0,4 Эрл. v=10.

Р₁=4,5‰ Р₂=8‰