§3.2. Общая теория регулярных линий передачи произвольного поперечного сечения. Поперечные и волноводные волны.

Рассмотрим распространение волн вдоль линии произвольной конфигурации (рис.3.2). В качестве основного ограничения примем неизменность размеров сечения и параметров линии в направлении передачи энергии. Такие линии принято называть регулярными. Поперечные размеры линии могут при этом находиться в любом соотношении с длиной волны.

Пусть поле распространяется в линии в направлении оси z и отсутствуют сторонние источники, следовательно, векторы электромагнитного поля E и H удовлетворяют однородным уравнениям Гельмгольца (2.16). Так как этим уравнениям будет удовлетворять и любая проекция векторов E и H, то для нахождения общих выражений составляющих поля необходимо решить одно скалярное дифференциальное уравнение второго порядка в частных производных типа

(3.1)

или в декартовой системе координат

где - любая из проекций векторов E и H.

Уравнение (3.1) можно решить методом разделения переменных. Представим его в виде произведения

,

где  - функция только x и y, называемая функцией формы или функцией сечения, а Z - функция z. Продифференцировав выражение для L, подставим его в (3.1). После деления на L получим:

. (3.2)

Поскольку первый член уравнения (3.2) зависит только от x и y, второй - только от z, а их сумма равна постоянной величине, естественно предположить, что и первый, и второй члены равны константе.

или , (3.3)

где - поперечный оператор Лапласа.

Подставив (3.3) в (3.2), получим уравнение для :

, (3.4)

где . (3.5)

Коэффициент  называется постоянной распространения; - поперечным или критическим волновым числом. Легко видеть, что уравнение (3.4) имеет решение вида

.

Уравнения (3.1) - (3.5) применимы к любой линии передачи, причем уравнение (3.3) определяет поле в поперечном сечении линии передачи.

Выражение для функции формы находится путем наложения на уравнение (3.3) конкретных граничных условий.

Рассмотрим наиболее общий вид колебаний, возможный в линии передачи, когда существуют все компоненты составляющих поля. Обратимся к первым двум уравнениям Максвелла для гармонического поля, положив, что диэлектрические и магнитные потери отсутствуют:

(3.6)

Разложив уравнения для роторов по осям координат и приняв во внимание, что и (пренебрегая отраженной волной), можно выразить поперечные составляющие поля через продольные следующими формулами:

(3.7)

Т

(H-волны),

аким образом, для определения компонент поля следует отыскать функцию  для продольной составляющей поля, положив

(E-волны),

а затем через нее выразить остальные (поперечные) компоненты поля.

Поперечные (tem) электромагнитные волны

Поскольку у поперечных волн продольные составляющие , то из выражений (3.7) следует, что они могут существовать только при условии . В этом случае и любая составляющая поля имеет вид:

. (3.8)

Подставив (3.8) в (3.1), получим , или в общем виде

, . (3.9)

Уравнения (3.9) - двумерные векторные уравнения Лапласа, которым, как известно, удовлетворяют векторы E и H статических полей.

Если совпадают граничные условия при определении полей TEM и статических полей, т.е. совпадают функции формы  этих полей, то достаточно рассмотреть решение соответствующей статической задачи, а потом распространить его на поле TEM-волны, добавив множитель . Очевидно, что TEM-волны могут существовать лишь в линиях, имеющих как минимум два изолированных проводника.

В силу потенциального характера поля TEM-волн металлические поверхности линии передачи являются эквипотенциальными для электрического поля, а силовые линии магнитного поля совпадают с электрическими эквипотенциалями.

В TEM-поле можно однозначно определить напряжение между двумя любыми точками поперечного сечения линии передачи и, в частности, между проводниками линии передачи (рис.3.3):

. (3.10)

Поскольку силовые линии магнитного поля лежат в поперечной плоскости, в линиях передачи с TEM-волной текут только продольные токи:

(3.11)

где - касательная составляющая вектора H; она при интегрировании может быть, в частности, взята на поверхности металлического проводника.

Характеристическое сопротивление в линиях передачи с TEM-волной определяется однозначно, в отличие от систем с волноводными волнами . Для линии с TEM-волной справедливо

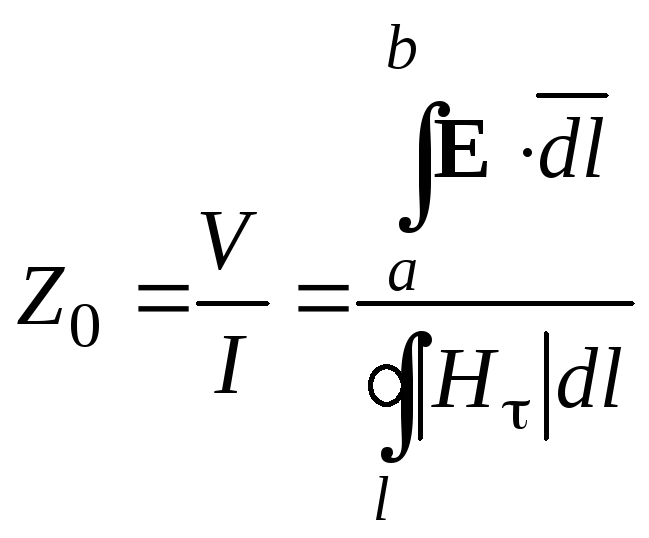. (3.12)

Величину называют также сопротивлением линии по току и напряжению.

Волновое сопротивление может быть найдено как отношение поперечных составляющих электрического и магнитного полей, определяемых непосредственно по (3.6),

, (3.13а)

и для другой комбинации составляющих:

, (3.13б)

здесь - собственное сопротивление среды. Легко видеть¹, что волновое сопротивление поперечных волн в линии передачи совпадает с волновым сопротивлением плоских волн, распространяющихся в бесконечной среде с параметрами  и .