Сферическая волна

В сферической системе координат (рис.1.8а) положение точки в пространстве определяется координатами: r,  и . При этом выражение для оператора Лапласа имеет вид

. (1.110)

Ограничимся рассмотрением поля с центральной симметрией. При этом зависимостей от углов (полярного θ и азимутального φ) не будет. Частные производные по углам в (1.110) равны нулю. Используя только первые два слагаемых в (1.110), из (1.61) получим:

. (1.111)

здесь - любая из составляющих поля.

Уравнение (1.111) посредством подстановки приводится к виду

. (1.112)

Решение последнего уравнения нам известно. В результате, переходя к искомой функции, получим

. (1.113)

При знаке “-” решение представляется в виде расходящихся сферических волн. Сферичность волны связана с тем, что фазовый фронт в сферических координатах представляет собой сферическую поверхность с центром в начале координат. Важнейшей особенностью сферической волны является то, что ее амплитуда зависит от координат, а именно, обратно пропорциональна расстоянию до начала отсчета.

Представление решения волнового уравнения в виде сферической волны удобно использовать, когда источник волн можно считать точечным, то есть, когда расстояние от точки наблюдения до источника много больше линейного размера источника. Непосредственно форма (1.113) применима к изотропному источнику, равномерно излучающему волны во все направления, однако, модель сферической волны можно применить и к анизотропному источнику, примером, служат формулы (1.77) и (1.79).

Применение же условия, аналогичного (1.107), приводит к следующим результатам. Пусть

,

тогда ,

и

.

Откуда следует, что необходимым условием является

. (1.114)

Из условия (1.114) следует, что у сферической волны отсутствует радиальная компонента поля¹, т.к. , то, следовательно, для удовлетворения условию (1.114) необходимо, чтобы !

Напряженность магнитного поля может быть найдена из уравнения Максвелла

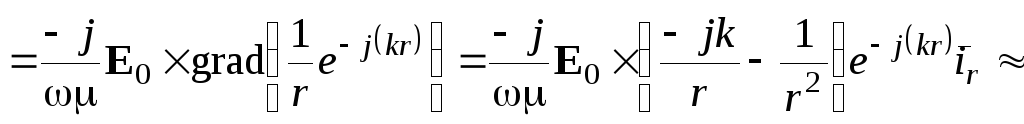
.² (1.115)

Цилиндрическая волна

В цилиндрической системе координатами, определяющими положение точки в пространстве являются азимутальный угол φ, радиус ρ и координата z (рис.1.15).

Волновое уравнение здесь будет выглядеть следующим образом:

, (1.115)

здесь - любая из компонент поля. Рассмотрим поле с осевой симметрией и не зависящее от координаты z. При этом в правой части (1.115) остается только первое слагаемое. Тогда для функции от радиуса будем иметь уравнение:

, (1.116)

здесь - любая из составляющих поля.

Данное уравнение является уравнением Бесселя. В простейшем случае его решением является функция Бесселя первого рода, нулевого порядка . Поведение функции Бесселя в зависимости от безразмерного аргумента х показано на рис. 1.16.

Как можно видеть из графика, при больших значениях аргумента функция ведет себя подобно тригонометрическим функциям синуса или косинуса с убывающей с ростом аргумента амплитудой. На самом деле решение уравнения типа (1.116) может быть представлено и функцией Бесселя второго рода , график которой представлен на рисунке 1.17. Полное решение с учетом временной зависимости можно записать в виде:

(1.117)

Очевидно, фазовая поверхность kρ = const представляет собой цилиндрическую поверхность. Естественно, что такая волна называется цилиндрической. В противоположность точечному источнику, порождающему сферические волны, цилиндрические волны описывают волновое поле на расстояниях от линейного источника, много меньших его длины.

Плоские и сферические волны, описанные здесь, соответствуют бегущим волнам, в то время как цилиндрическая волна в форме (1.117) является стоячей [7]. Скомпоновать плоские и сферические стоячие волны не представляет труда. Необходимо только разделить временные и пространственные части и представить их в виде соответствующих тригонометрических функций. Несколько сложнее обстоит дело с представлением бегущей цилиндрической волны. Необходимо исходить из того, что функции Бесселя первого и второго рода имеют асимптотики при больших значениях аргумента в виде косинуса и синуса, соответственно, и с амплитудой, обратно пропорциональной аргументу. Тогда, в соответствии с тригонометрическими тождествами

cos(a – b) = cos(a)cos(b) + sin(a)sin(b)

и sin(a – b) = cos(a)sin(b) - sin(a)cos(b),

бегущая цилиндрическая волна должна быть записана в виде:

, (1.118)

При знаке “-” решение представляется в виде расходящихся цилиндрических волн.

На оси цилиндра такое решение имеет особенность (обращается в бесконечность).

Для достаточно больших значений kρ функции Бесселя представимы в виде

,

.

Тогда общее решение (1.118) преобразуется к виду

. (1.118)

Плоские, сферические и цилиндрические волны являются модельными описаниями волновых полей [7]. Для конкретных задач та или иная модель становится предпочтительной. В то же время любое «достаточно хорошее» волновое поле может быть описано любой из этих моделей. Дело в том, что и тригонометрические функции, используемые в плоских и сферических волнах, и бесселевы функции в цилиндрических волнах являются ортогональными. Следовательно, любую, опять же «достаточно хорошую», функцию можно разложить в интеграл Фурье или интеграл Фурье–Бесселя.