Глава 8. Сложное движение

8.1. Сложное движение точки

Примером сложного движения точки может служить:

а) лодка (если ее принять за материальную точку), плывущая от одного берега реки к другому;

б) шагающий по ступенькам движущегося эскалатора метро че­ловек, который также совершает сложное движение относительно неподвижного свода туннеля.

Таким образом, при сложном движении точка, двигаясь относи­тельно некоторой подвижной материальной среды, которую условимся называть подвижной системой отсчета, одновременно передвигается вместе с этой системой отсчета относительно второй системы от­счета, условно принимаемой за неподвижную.

Движение некоторой точки М по отношению к подвижной системе отсчета называется относительным. Движение подвижной системы от­счета вместе со всеми связанными с ней точками материальной сре­ды по отношению к неподвижной системе отсчета для точки М называется переносным. Движение точки М по отношению к неподвижной системе отсчета называется сложным, или абсолютным.

Для того чтобы видеть сложное (абсолютное) движение точки, наблюдатель сам должен быть связан с неподвижной системой отсче­та. Если же наблюдатель находится в подвижной системе отсчета, то он видит лишь относительную часть сложного движения.

Представим, что точка М за некоторое время переместилась от­носительно подвижной системы координат O₁X₁Y₁ из начального по­ложения M₀ в положение М₁ по траектории M₀М₁ (траектории относительного движения точки) (рис. 8.1). За это же время Δt подвижная система координат O₁X₁Y₁ вместе со всеми неизменно связанными с ней точ­ками, а значит, и вместе с траекторией относительного движения точки М переместилась в неподвижной системе координат OXY в но­вое положение:

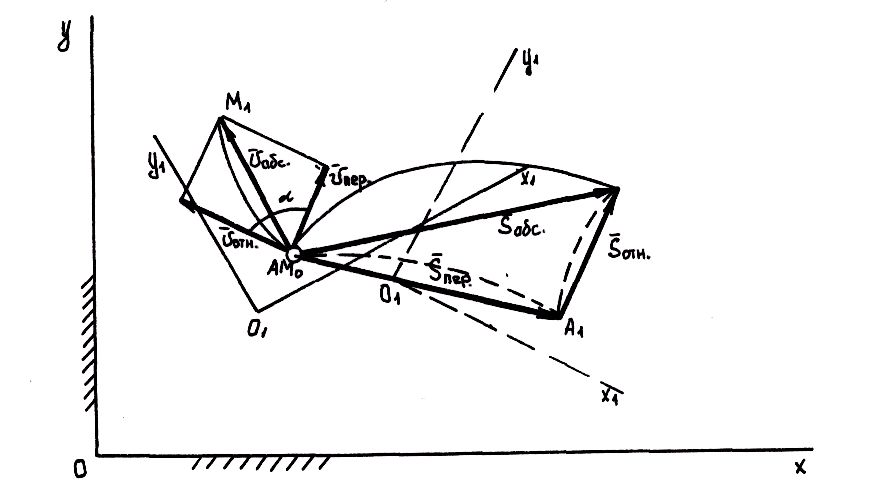
Рис. 8.1. К анализу сложного движения точки

Разделим обе части этого равенства на время движения Δt:

и получим геометрическую сумму средних скоростей:

,

которые направлены вдоль соответствующих векторов перемещений. Если теперь перейти к пределам при , то получим уравнение

выражающее теорему сложения скоростей: при сложном движении точ­ки абсолютная скорость в каждый момент времени равна геометри­ческой сумме переносной и относительной скоростей.

Если задан угол , то модуль абсолютной скорости

Углы, образуемые векторами абсолютной скорости с век­торами и , определяются по теореме синусов.

В частном случае при при сложении этих скоростей образуется ромб (рис. 8.2,а) или равнобедренный треугольник (рис. 8.2, б) и, следовательно,

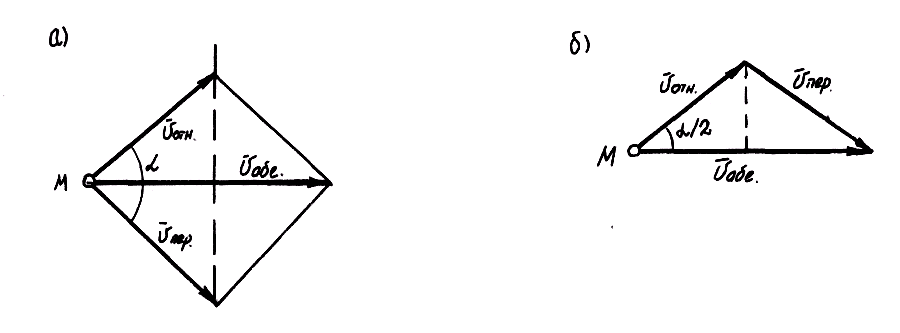
а б

Рис. 8.2. Частный случай

8.2. Плоскопараллельное движение тела

Движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости, назы­вается плоскопараллельным (рис. 8.3).

Рис. 8.3. Плоскопараллельное движение твердого тела

Изучая плоскопараллельное движение тела М, достаточно рас­сматривать движение его плоского сечения q плоскости ХОY (рис. 8.4).

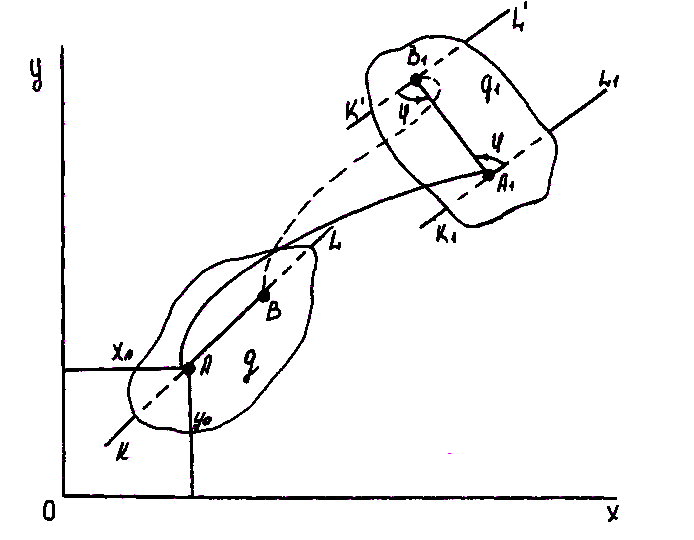
Рис. 8.4. К анализу плоскопараллельного движения твердого тела

Выберем в сечении q произвольную точку A, которую назовем полюсом. С полюсом А свяжем некоторую прямую KL, а в самом се­чении вдоль прямой KL проведем отрезок AB, перемещая плоское сечение из положения q в положение q₁. Можно сначала передви­нуть его вместе с полюсом А поступательно, а затем повернуть на угол φ.

Плоскопараллельное движение тела – движение сложное и состоит из поступательного движения вместе с полюсом и вращательного движения вокруг полюса.

Закон плоскопараллельного движения можно задать тремя уравнениями:

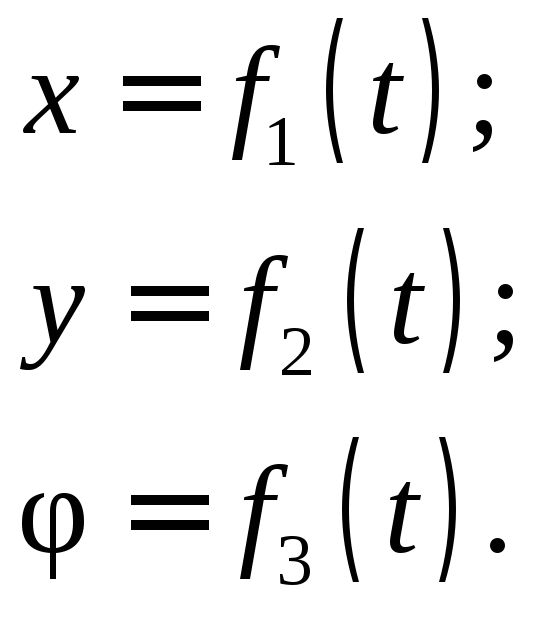
Дифференцируя заданные уравнения плоскопараллельного движе­ния, можно в каждый момент времени определить скорость и ускорение полюса, а также угловую скорость и угловое ускорение тела.

Пример 8.1. Пусть движение катящегося колеса диаметром d (рис. 8.5) за­дано уравнениями

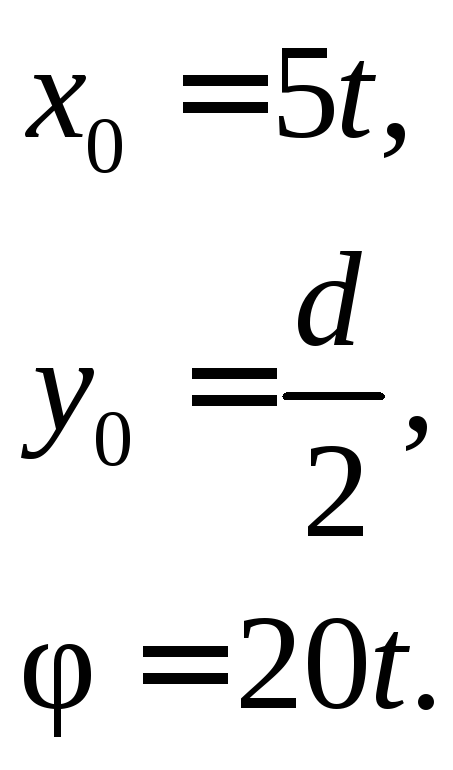
где и – м, φ – рад, t – с.

Продифференцировав эти уравнения, нахо­дим, что скорость полюса O угловая ско­рость колеса Ускорение полюса и угловое ускорение колеса в данном случае равны нулю. Зная скорость полю­са и угловую скорость тела, можно затем определить скорость лю­бой его точки.

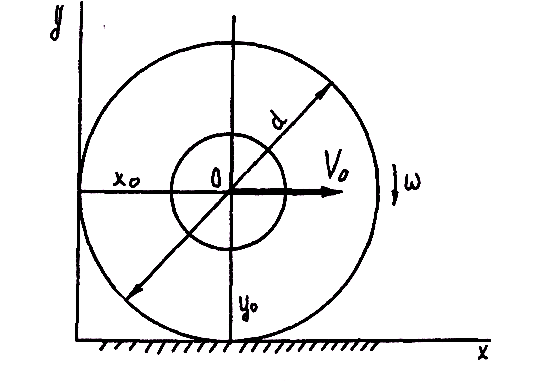
Рис. 8.5. К примеру 8.1