9.11 Snooker

Context

Television exposure has made snooker very popular. The expertise of the game's best players continues to be impressive and they can usually be relied upon to pot the balls from all distances and angles. Advice to beginners is to practise hard and often, until you learn how to strike the cue ball so that after impact the coloured ball is sent off at just the correct angle and speed to enter a pocket. Can a mathematical model help to give advice to beginners on where to aim with the cue ball and consequently play better snooker?

The pockets are narrow, but there is a little margin of error which allows a ball to enter a pocket even if your aim is not quite perfect. Human error is always present; so an interesting question is how much deviation can be allowed on a shot while still allowing the coloured ball to enter the pocket. Advice can then be given to the player on where to aim with the cue ball and beginners can learn how to play better snooker.

Problem statement

To fix ideas, a particular problem will be considered. We shall suppose that only the pink and black balls remain to be potted and that they are on their marker spots on the table. Let us suppose that the white cue ball happens to be on the table centre spot. This is shown in Figure 9.22.

The dimensions of a snooker table are required and the necessary data have been marked in the diagram. The problem that we wish to solve is quite simply stated as ‘How should the pink be potted, followed by the black in the easiest possible manner?’ This means that we can obviously concentrate first on potting the pink.

Formulate a mathematical model

There are two features to be considered by the player as he sets out to strike the cue ball: where to aim and how fast to hit the cue ball. He may also be skilful enough to put some ‘side’ spin on the cue ball so that a good position can then be obtained for potting the black in the next shot. However, the investigation here will not take spin into account as the mathematics becomes a little difficult for an initial model.

The two issues of speed and direction can be separated in the first place. Looking at the directional problem, we quickly realise that this will involve geometrical work only—a mathematical model for the impact between snooker balls can be left until later. We assume that the pink ball moves off in the

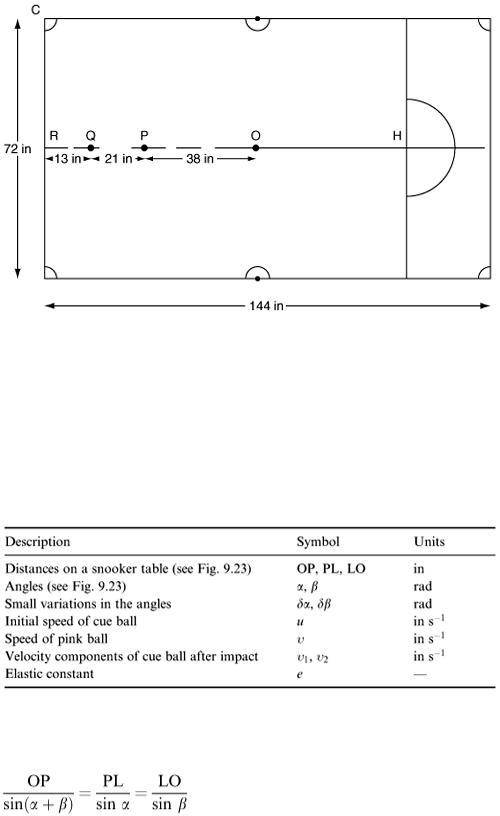
Figure 9.22

direction of the collision impulse of the two balls, and in turn this impulse will be taken always along the line joining the centres of the colliding balls, as they are assumed to be smooth. The problem is illustrated in Figure 9.23.

From Figure 9.23, it can be seen that the cue ball is aimed at an angle α to the initial line of centres and that the pink is then sent off towards the pocket C at an angle β. Our problem is to relate α to β, and to find how much variation is possible in making the shot so that the ‘pot’ is successful. We now list our variables in Table 9.18.

Table 9.18

Obtain the mathematical solution

By using the ‘sine’ rule of trigonometry applied to the triangle OPL,

(9.28)

A snooker ball has a diameter of 2.125 in; so, taking the data from Figure 9.22 we can substitute into equation (9.28) to get

Figure 9.23

Rearrangement of this gives, from the first pair of equations,

(9.29)

Now β will be known from the table measurements as tan −1 (18/17) but, before using this value, we realise that it is the perturbations on α and β that are of interest. Denote a small change in α by δα and a similar small change in β by δβ; then, by differentiating equation (9.29)

Substituting for α from equation (9.29), after a little manipulation we find that the formula relating the small changes in α and β is

Using β = tan −1 (18/17), this reduces to

(9.30)

This equation can be used to answer the first question on the accuracy of the shot. The entry to the pocket on a snooker table is of total width 3.0 in. Without discussing situations where the ball glances off the edge of the pocket and still drops in (notoriously unreliable!), this means that δβ can be calculated as shown in Figure 9.24.

We find that δβ = 0.008829 (measured in radians). Hence, using equation (9.30), δα = 0.000336 rad.

This is a very tiny deviation. Its value can be expressed as a percentage change permitted in α, which itself is small. From equation (9.29),

since β = tan −1 (18/17). The percentage deviation is (δα/α) × 100 = 0.8%.

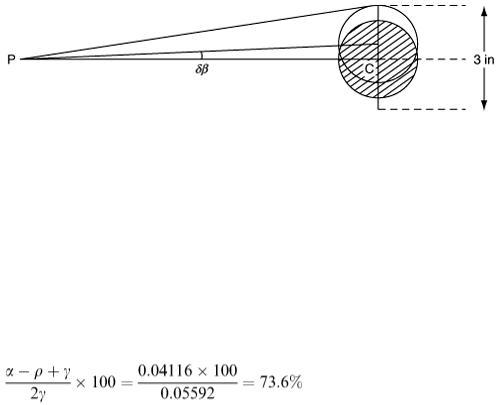
Allowing for possible data inaccuracies and so on, we can say that the permitted deviation is about 1%; so the shot has to be struck very accurately.

Figure 9.24

Interpret the mathematical solution

From the point of view of the player, knowing the angle of impact and the error allowed does not necessarily help in lining up the shot. As the player bends across the table to strike the cue ball, it is the amount of obliqueness of the impact that has to be judged; it does not really help to know that α = 0.042 26 rad. To evaluate the obliqueness, we need to say how much of the pink should be visible from O as the balls collide. This is a slightly tricky point since the player sees the balls in line from a point some way back from O, and his eye will probably be above the plane of the table.

From Figure 9.25 the angles γ and ρ are easily worked out by simple trigonometry to be γ = 0.02796 rad and ρ = 0.02906 rad. Hence, if we look at the pink from O, the percentage of the ball visible is

Thus, we have answered the next question, i.e. the fact that the obliqueness necessary is for about three-quarters of the pink to be visible from O.

We now turn our attention to the second part of the problem, namely the potting of the black ball. The path of the cue ball must be modelled first, which brings us to the question of how snooker balls behave on collision. For oblique impact, there are three properties of mechanical systems that can be applied.

1. Total linear momentum is conserved along the line of centres of the two balls.

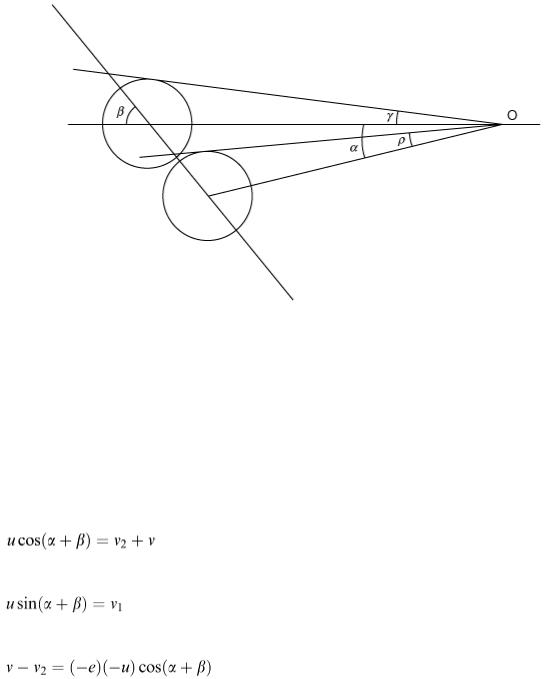
Figure 9.25

2.

The linear momentum of each ball is separately conserved in a direction perpendicular to the impulse.

Newton's impact rule can be used; this states that the relative velocity after impact is proportional to the relative velocity before impact in a direction along the line of centres, where the constant of proportionality represents the elasticity of the materials in collision.

Application of (a)–(c) will enable the speed and direction of the cue ball after impact to be calculated. A diagram is necessary to help to follow the application (Figure 9.26). In relation to the symbols marked in Figure 9.22, we have, from (a),

(9.31)

from (b),

(9.32)

and, from (c),

(9.33)

A value is needed for the elastic constant e. It is possible that the cue ball will also strike the side cushion in its motion after colliding with the pink ball. Also, what will be a suitable value for the velocity of the cue ball just before impact? The following data are reasonably representative.

1.The elastic constant between two snooker balls equals 0.6.

2.The elastic constant between a ball and a cushion equals 0.8.

3.In motion along the table a snooker ball experiences a constant retardation of 0.7 ft s −2 (obtained by trial).

4.u is chosen so that the pink just drops in the pocket.

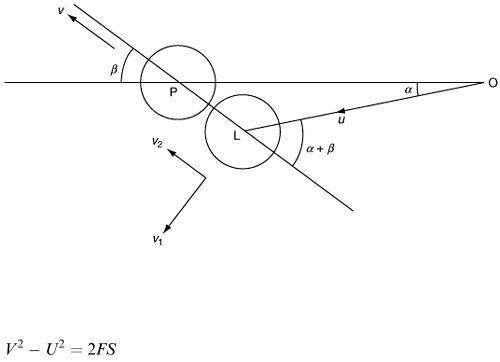
Figure 9.26

The motion of the cue ball can now be charted using the simple formula from particle kinematics which applies to motion with constant acceleration:

(9.34)

(here U is the initial speed, V is the final speed, F is the acceleration and S is the distance travelled). Now, as the pink just falls into the pocket, from equation (9.34) we get

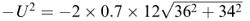i.e. U = 28.8 in s −1 . However, α = 0.04226 rad and β = 0.81396 rad; so, from equations (9.31) and (9.33), u = 55.02 in s −1 .

The speed of the cue ball can now be calculated. From equations (9.31)− (9.33) v 1 = 41.56 in s −1 and v 2 = 7.21 in s −1 . These are velocity components with respect to the line PL. It is easier if the motion of the cue ball is related to OP, and a simple calculation gives the velocity component down the table as 35.17 in s −1 and that across as 23.29 in s −1 which on combining gives a velocity of 42.18 in s −1 at an angle of 33.51 rad with PR.

Now it is clear from the dimensions of the snooker table that the cue ball is heading for the back cushion. By using equation (9.32) we can calculate that the impact occurs with a speed of 32.88 in s −1 , at a distance of 20.05 in from the corner pocket. The cue ball then rebounds from this cushion with its velocity component normal to the cushion reduced by the factor 0.8 (specified earlier as the elastic constant between the ball and a cushion). Continuing in this way, the cue ball next rebounds off the side cushion and finally comes to rest at a point O′ 36.38 in from the end cushion and 15.95 in from the side. This is shown in Figure 9.27.