−2 and the (abbreviated) SI units for force are kg m s −2 (defined to be 1 N). In ordinary conversation, it is very common to use ‘mass’ and ‘weight’ as equivalent terms but do not confuse the two. The weight of an object is the force exerted on it by the Earth's gravitational field. It is an experimental fact that, near the Earth's surface, all bodies in free fall accelerate at the constant rate of g 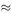9.806 65m s −2 or 32.174 ft s −2 . Consequently the weight of a mass of m kg is mg N. It may be helpful to think of a force of 1 N as the weight of a fairly large apple (mass of about 0.1 kg).

Any sensible equation must be dimensionally consistent, i.e. [left-hand side] = [right-hand side]. It is a good idea to carry out this check on all the equations appearing in a model. Modelling errors can often reveal themselves in this way. Note that any constants appearing in our equations can be dimensionless (i.e. pure numbers) or can have dimensions. For example, suppose that we are modelling the force on a moving object due to air resistance. If we assume the magnitude of the force F is proportional to the square of the speed v, this leads to a model of the form F = kv 2 . Checking the dimensions of this equation, we have [ F ] = [ kv 2 ], i.e.

For consistency, we require [ k ] = ML −1 and k will be measured in kg m −1 .

Note that if expressions involving exp( at ) or sin( at ) appear in our model, where t stands for time, the parameter a must have dimensions T −1 so that at is a dimensionless number.

If an equation involves a derivative, the dimensions of the derivative are given by the ratio of the dimensions.

For example, if p is the pressure in a fluid at any point, the pressure gradient in the direction of z is d p /d z and

Similarly, for partial derivatives,

and

4.10 Dimensional analysis

This is a method of using the fact that the dimensions of each term in an equation must be the same to suggest a relationship between the physical quantities involved. This will not give the exact form of a function but is still useful. Suppose that we are trying to develop a model which will predict the period of a swinging pendulum. A list of the factors involved might include the length l, the mass m, the acceleration g due to gravity, the amplitude θ, air resistance R and the rotation of the Earth. If we restrict this list to the first four factors, we can assume that the period t is given by some function of the four factors. Assume that t = kl a m b g c θ d ], where a, b, c, d and k are real numbers. Considering dimensions, we have

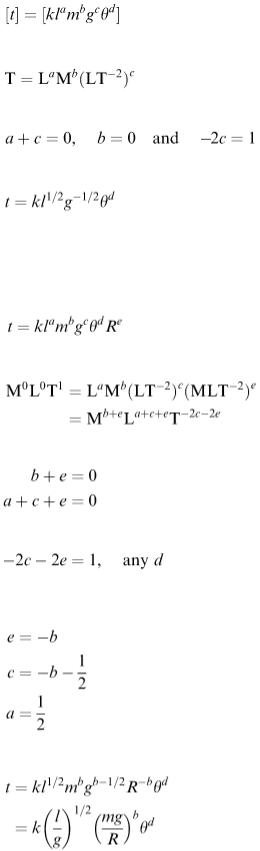
and so

( k and θ are dimensionless). Equating powers of M, L and T on both sides, we must have

This gives

In this expression, d could take any value and we could sum terms of this form to arrive at t = f (θ) l 1/2 g −1/2 . We have to find f (θ) some other way. For small θ, of course, f (θ) is approximately constant with value 2π.

If we also include the force R due to air resistance, our model becomes

and so

We require

and

We now have three equations with four unknowns. We could write any three of them in terms of the fourth. Suppose that we write everything in terms of b. We have

So

which generalises to

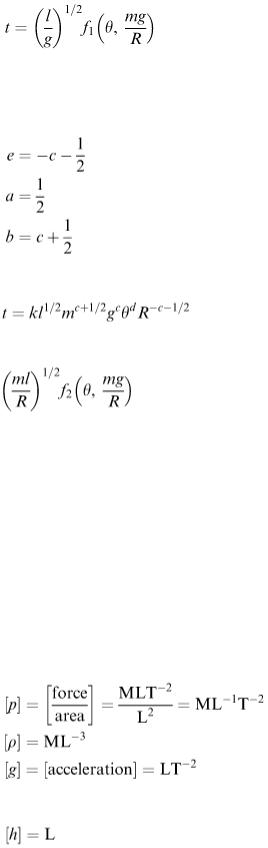
for some function f 1 .

Returning to the three equations with four unknowns, if we express all the parameters in terms of c, we have

giving

or

for some function f 2 .

In both of these expressions for t, we have a time factor multiplied by a function of the two dimensionless quantities, θ and mg/ R. The time factors are ( l/g ) 1/2 and ( ml/R ) 1/2 . The first of these gives a time scale associated with the period of oscillation and the second gives a time scale associated with the damping due to air resistance. The quantity mg/R is a dimensionless combination of physical quantities and is an example of a dimensionless group. This is a useful concept in modelling physical systems. In fluid mechanics a very useful dimensionless group is the Reynolds number ( Re ) = ρ ul /μ, where l is a characteristic length in the problem (e.g. the diameter of a pipe), ρ is the density of the fluid, μ is its viscosity and u is the fluid speed.

Example 4.9

The pressure p at a depth h below the surface of a fluid of density ρ is given by p = ρ gh, where g is the acceleration due to gravity. We can check that this equation is dimensionally correct as follows:

and

So 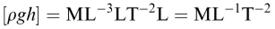as required.

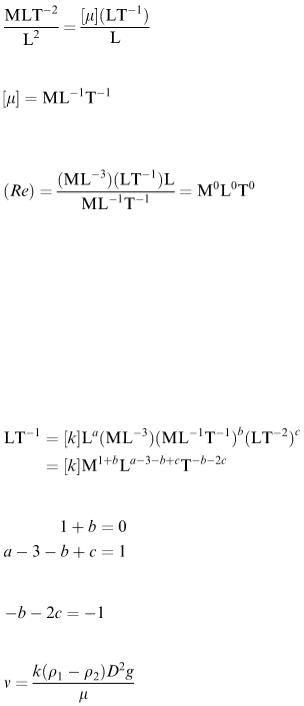
Example 4.10

The fluid viscosity μ is defined by the relation force per unit area = μ × velocity gradient in the direction perpendicular to the area. If we take the dimensions of both sides of this relation, we have

So

and μ is measured in kilograms per metre per second (kg m −1 s −1 ). The dimensions of ( Re ) = ρ ul / μ are

i.e. ( Re ) is a dimensionless group as previously stated. Example 4.11

When a particle falls under gravity in a viscous fluid, the drag that it experiences counteracts the acceleration due to gravity and after a while the particle's speed stops increasing. When this happens, we say that it has reached its ‘terminal speed’. For a finite spherical particle, it is reasonable to suppose that the terminal speed v depends on the particle's diameter D, the viscosity μ of the fluid and the acceleration g due to gravity. Suppose also that v is directly proportional to the difference between the density ρ 1 of the particle and the density ρ 2 of the fluid. We assume that v = kD a (ρ 1 − ρ 2 )μ b g c .

Taking dimensions of both sides, we have

If k is a dimensionless number, then

and

So b = − 1, c = 1, a = 2 and our model is

Theoretical analysis using the laws of hydrodynamics leads to v = (ρ 1 − ρ 2 ) D 2 g /18μ, an expression known as ‘Stokes’ drag’. This clearly fits with our expression obtained from simple dimensional considerations.

Exercises

4.23 Newton's gravitational law states that F = Gm 1 m 2 / r 2 , where F is the magnitude of the

gravitational force of attraction between two masses m 1 and m 2 separated by a distance r. What are the units of the gravitational constant G ?

In a compressible fluid, the bulk modulus K is defined as

4.24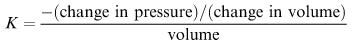

What are the dimensions of K ?

Which of the following equations contain an error and which are dimensionally correct?

1.

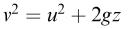
2.

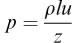
4.25

3.

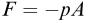
4.

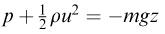
p is a pressure, ρ is a density, u and v are velocities, F is a force, m is a mass, A is an area, and z and l are lengths.

The following models are meant to predict the volume flow rate Q of fluid through a small hole in the side of a large tank filled with fluid to a height H above the hole. Which one is dimensionally correct?

4.261.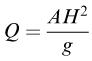

2.

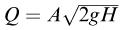
3.

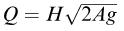
A is the cross-sectional area of the hole and g is the acceleration due to gravity.

4.27 Check that the equation