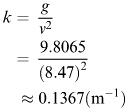
quantity has dropped to 10% of its peak value, then the turf is dry enough. How long we have to wait is given by putting Q = 0.000835 in equation (9.15), i.e. 0.000835 = 0.124 exp(−0.0015 t ). Taking logarithms, we find that −7.08808 = −2.0875 − 0.0015 t, giving t = 3334. So, after the end of the shower, we shall have to wait a further 1534 s or about 16 min.

Our choice of 10% was rather arbitrary. How much longer would it take to get down to 5% of the maximum? With Q = 0.004175 in equation (9.15) we find that t = 3796; so a further 462 s or about 8 min is required.

9.8 Parachute jump

Context and problem statement

When a parachute jump is made from an aeroplane, quite often the first part of the descent is made in ‘free fall’ at a high altitude. After a certain time the parachutist then opens the parachute to enable a soft landing to be completed. The important question for the parachutist is to decide when the parachute should be opened. This must obviously not be too late; otherwise the landing speed will be too great, resulting in injury or death of the performer. On the other hand, at a great altitude with a thin atmosphere a free fall can generate high speeds, which can add to the exhilaration of the event. There may also be reasons for not opening the parachute immediately owing to the proximity of the aeroplane and other parachutists. It is therefore interesting to model the motion of the parachute jump and to see whether there is some optimum position at which the parachute should be opened.

Suppose that the aeroplane is travelling horizontally at a height of 500 m with a speed of 125 m s −1 . The mass of the person jumping together with the parachute seems like a data requirement, but it turns out that it is more important for the simulation to make accurate assessments of the air resistance and the obvious change in air drag when the parachute is opened. The idea of terminal speed is important again (see sections 4.9 and 6.3). The terminal speed of a human in free fall will be taken as 120 miles h −1 . Now obviously the parachutist needs to make a soft landing; from information concerning jumps the usual comment is that a parachute landing should be like falling off a 12 ft wall. This means that the terminal velocity with the parachute open must be the same as the velocity acquired on falling off the wall. Now, from simple energy considerations on falling through a height h (and neglecting air resistance over a small distance), the velocity v is given by v 2 = 2 gh. Here h = 12 ft = 12 × 12/39.37 m. Also g = 9.8065 m s −2 ; so v 2 = 2 × 9.8065 × 12 × 12/39.37, i.e. v 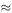8.47 m s −1 .

If we allow for air resistance proportional to the square of velocity, then, following the notation in section 8.3, the air resistance constant k is given by

(9.16)

The air resistance constant for the free-fall part of the drop can be calculated from the terminal velocity formula v = g/k, which is the case when the air resistance is taken directly proportional to velocity (again see section 8.3). This

is valid since the atmosphere is fairly thin at a great height and the falling human is relatively compact in shape. If we take the terminal velocity to be 120 miles h −1 as stated above, this converts to 53.645 m s −1 . Hence,

(9.17)

The equations of motion for the parachutist will be very similar to those in section 8.3 and the same notation can be followed.

Formulate a mathematical model

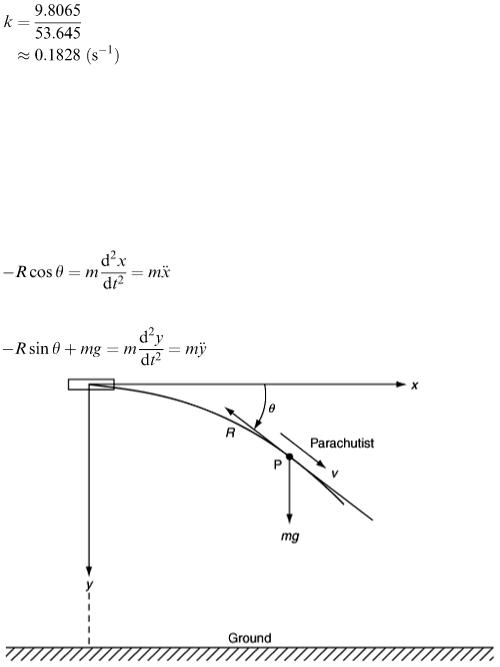
The diagram in Figure 9.16 helps to clarify the problem and define the required variables. The list of factors is given in Table 9.14.

Application of Newton's law of motion gives two equations: one for the horizontal motion and one for the vertical motion. For horizontal motion, we have

(9.18)

and, for vertical motion,

(9.19)

Figure 9.16

Table 9.14

*Provided that R is directly proportional to v .

Now R = mkv n , 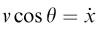and 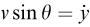, where 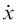and 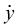are the components of velocity, and the exponent n will be taken as 1 for free fall and 2 for the effect once the parachute has opened.

Also from the components, we have the relation 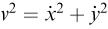. We can therefore eliminate v and θ to give

(9-20)

(9-21)

These two coupled simultaneous differential equations make up the general mathematical model for the parachute drop. They cannot be solved without a computer program to obtain approximate answers. In passing, note that the main assumption made so far is that the motion takes place entirely in one plane, denoted here by the axes O xy. Now, equations (9.20) and (9.21) are non-linear since they contain

powers of 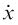and 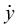However, for the first part of the motion, as we have already stated, if the assumption is made that the air resistance is directly proportional to velocity, then the exponent n = 1. This leads to some simplification of the equations so that, in fact, equations (9.20) and (9.21) can be integrated exactly.

Obtain the mathematical solution

With n = 1 for the first part of the motion, the equations to be solved are

and

where, from the data above, the value of k will be taken as 0.1828. Initial conditions are as follows: x

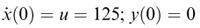(0) = 0 and and 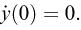Integrating twice in each case, it is easy to obtain the solutions

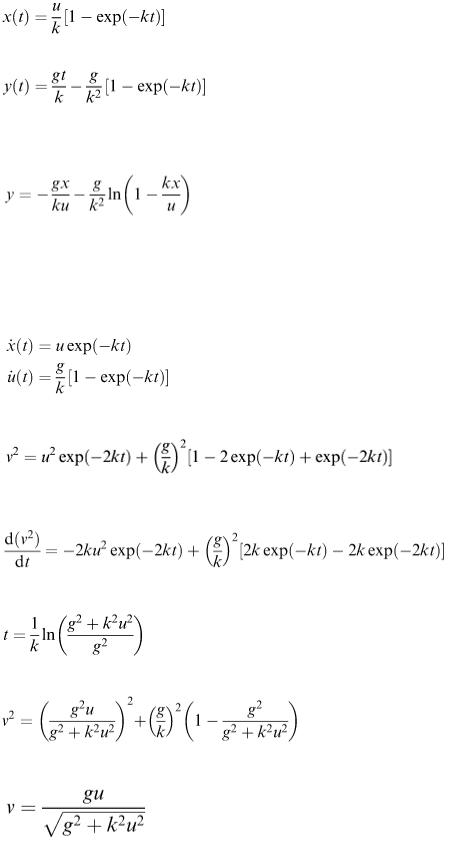
(9.22)

and

(9.23)

So long as the assumptions on air resistance hold and the parachute is not opened, then these two equations give the path of the falling person. In fact, y can be explicitly expressed in terms of x by eliminating t between equations (9.22) and (9.23): to give

(9.24)

A units check (see chapter 4) may be carried out so that, for example, we can be sure that a k has not been dropped in error. Also the well-known results for projectile motion in vacuo can be obtained from equation (9.24) by expanding it in a series and then putting k = 0. This is left for our readers to try out.

It is interesting to chart the velocity of the parachutist as the drop takes place. This can be done from the velocity equations obtained by differentiating equations (9.22) and (9.23)

Therefore,

(9.25)

If a graph is drawn of the behaviour of v as time elapses, it can be seen that v has a minimum value. This surprising result can be checked by differentiation:

d( v 2 )/d t = 0, for a minimum value of v 2 and also for v. Simplifying, we get

(9.26)

The speed at this time is easily obtained from equation (9.25) as

which simplifies to

(9.27)

Now the initial value of v is u and the terminal speed is g/k; so equation (9.27) can be checked against these two values to show that the speed of the parachutist reaches a minimum value, less than both the initial and the terminal velocities. On examining the inequalities, we can easily show that

and

From the data given, calculations using equations (9.26), (9.27), (9.22) and (9.23) can be carried out to show that in this case the parachutist reaches a minimum speed of 49.31 m s −1 after 10.18 s, when his position is x = 577.5 m and y = 298.4 m.

If we return to equations (9.20) and (9.21), it is possible to get computer solutions for these equations for general values of k and n. For instance, if the ‘linear’ model for free fall is rejected, and instead we take n = 2, then an alternative value of k is easily calculated from the terminal velocity relation g = kv 2

. It turns out that the parachutist still experiences decreasing velocity to some minimum value before speeding up again.

When the parachute is opened, there will be a sharp jerk due to the abrupt change in the resistance force. This force can be considerable (and probably unpleasant for the parachutist), which is why the decision can now be made to open the parachute when the speed is a minimum. We can calculate this change in force which causes the jerk from the difference between the values of R before and after the opening. Before the opening.

and, after the opening,

The difference is about 300 m (N) which is large, but on the other hand the parachute will not be opened instantaneously; so this change may be spread over several seconds.

Table 9.15

To simulate the remainder of the descent, equations (9.20) and (9.21) must be solved in the case where k = 0.1367 and n = 2. As the height of the jump was taken to be 500 m, there is about 200 m left to fall.