
- •1 Билет
- •1. Общая классификация сигналов.
- •2. Элементы цепей синусоидального тока. Резистор.
- •3. Интегрирующие цепи.
- •2 Билет
- •1. Импульсные сигналы.
- •2. Элементы цепей синусоидального тока. Конденсатор.
- •3. Преобразование Лапласа и его свойства.
- •1. Классификация сигналов по структуре и соответствующие им цепи.
- •2. Элементы цепей синусоидального тока. Катушка индуктивности.
- •3. Операторный метод анализа линейных стационарных систем.
- •4 Билет
- •1. Классификация цепей. Свойства линейных цепей с постоянными параметрами.
- •2. Общие комплексные сопротивления и проводимости цепей синусоидального тока.
- •3. Свойства передаточной функции. Формула обращения.
- •5 Билет
- •1. Свойства параметрических и нелинейных цепей. Этапы анализа цепей.
- •2. Последовательное соединение элементов цепи синусоидального тока.
- •3. Аналитические свойства входного сопротивления двухполюсника.
- •6 Билет
- •1. Элементы теории ортогональных сигналов.
- •2. Параллельное соединение элементов цепи синусоидального тока.
- •3. Синтез пассивных двухполюсников. Метод Фостера.
- •7 Билет
- •1. Связь обобщенного ряда Фурье и энергетических характеристик сигнала.
- •2. Резонанс напряжений.
- •3. Синтез пассивных двухполюсников. Метод Кауэра.
- •8 Билет
- •1. Гармонический анализ периодических сигналов.
- •2. Резонанс токов.
- •3. Четырехполюсники и их классификация.
- •9 Билет
- •1. Гармонический анализ непериодических сигналов. Преобразование Фурье.
- •2. Энергетический анализ цепей синусоидального тока.
- •3. Системы y и н параметров четырехполюсников.
- •10 Билет
- •1. Свойства преобразования Фурье. Сдвиг сигнала во времени и по частоте.
- •2. Согласование источника энергии с нагрузкой.
- •3. Системы z и а параметров.
- •11 Билет
- •1. Свойства преобразования Фурье. Изменение масштаба времени, дифференцирование и интегрирование колебаний.
- •2. Основные параметры цепей с индуктивно-связанными элементами.
- •3. Передаточная функция четырехполюсника и ее свойства.
- •12 Билет
- •1. Свойства преобразования Фурье. Сумма и произведение двух колебаний.
- •2. Индуктивная связь двух катушек.
- •3. Минимально-фазовые и неминимально-фазовые цепи. Коэффициент передачи мощности четырехполюсника.
- •13 Билет
- •1. Свойства преобразования Фурье. Взаимная заменяемость частоты и времени в преобразованиях Фурье.
- •2. Вариометры.
- •3. Фильтры и их общая классификация.
- •14 Билет
- •1. Распределение энергии в спектрах периодических сигналов.
- •2. Идеальный трансформатор.
- •3. Классификация фильтров по полосе пропускания.
- •15 Билет
- •1. Линейные цепи постоянного тока. Основные определения.
- •2. Элементы трехфазных систем. Симметричные и уравновешенные системы.
- •3. Алгоритм проектирования фильтров и допустимые пределы отклонения характеристик.
- •16 Билет
- •1. Элементы цепей постоянного тока. Резистор.
- •2. Соединение трехфазной системы звездой.
- •3. Фнч. Фильтр Баттерворта.
- •17 Билет
- •1. Элементы цепей постоянного тока. Катушка индуктивности.
- •2. Соединение трехфазной системы треугольником.
- •3. Фнч. Фильтр Чебышева.
- •18 Билет
- •1. Элементы цепей постоянного тока. Конденсатор.
- •2. Расчет симметричных режимов работы трехфазных систем.
- •3. Структурный синтез фнч.
- •19 Билет
- •1. Схемы замещения источников электрической энергии.
- •2. Расчет несимметричных режимов работы трехфазных систем.
- •3. Реализация фвч и пф.
- •20 Билет
- •1. Топологии цепей. Основные понятия.
- •2. Метод симметричных составляющих.
- •3. Передаточная функция системы с ос.
- •21 Билет
- •1. Топологии цепей. Матрицы соединений.
- •2. Свойства симметричных составляющих токов, напряжений и сопротивлений различных последовательностей трехфазных систем.
- •3. Устойчивость цепей с ос.
- •22 Билет
- •1. Законы Кирхгофа в линейных цепях.
- •2. Мощность трехфазных цепей.
- •3. Операционный усилитель.
- •23 Билет
- •1. Закон Ома для участка цепи с эдс.
- •2. Простейшие разрывные функции и их свойства.
- •3. Принцип построения активных rc-фильтров.
- •24 Билет
- •1. Правила делителей напряжения и тока.
- •2. Линейные стационарные системы и их математические модели.
- •3. Задача оптимальной фильтрации. Отношение сигнал/шум.
- •25 Билет
- •1. Эквивалентные преобразования линейных электрических цепей.
- •2. Импульсная характеристика линейной стационарной системы. Интеграл Дюамеля.
- •3. Критерий оптимальности линейного частотного фильтра.
- •26 Билет
- •1. Метод наложения.
- •2. Переходная характеристика линейной системы и ее связь с импульсной.
- •3. Согласованный линейный фильтр.
- •27 Билет
- •1. Метод эквивалентного генератора.
- •2. Частотный коэффициент передачи линейной стационарной системы.
- •3. Частотный коэффициент передачи согласованного фильтра.
- •28 Билет
- •1. Метод уравнений Кирхгофа.
- •2. Линейные динамические системы. Частотный коэффициент передачи линейной динамической системы.
- •3. Безынерционные нелинейные преобразования.
- •29 Билет
- •1. Метод контурных токов.
- •2. Законы коммутации в электрических цепях.
- •1 Закон коммутации:Ток в индуктивном элементе скачком измениться не может, т.Е. Ток до момента коммутации должен быть равен току в момент коммутации: .
- •3. Характеристики нелинейных элементов.
- •30 Билет
- •1. Метод узловых потенциалов.
- •2. Классический метод анализа переходных процессов.
- •3. Аппроксимация нелинейных характеристик.
- •31 Билет
- •1. Однофазные цепи синусоидального тока. Основные понятия.
- •2. Коэффициент передачи многокаскадных систем. Частотный коэффициент передачи мощности.
- •3. Воздействие гармонических колебаний на цепи с безынерционными нелинейными элементами.
- •32 Билет
- •1. Изображение синусоидальных функций в декартовой плоскости. Векторные диаграммы.
- •2. Спектральный метод анализа линейных стационарных систем.
- •3. Бигармоническое воздействие на нелинейные элементы.
- •33 Билет
- •1. Комплексные изображения синусоидальных функций.
- •2. Дифференцирующие цепи.
- •3. Классификация фильтров по полосе пропускания.
2. Спектральный метод анализа линейных стационарных систем.
НЕТ!!
3. Бигармоническое воздействие на нелинейные элементы.
НЕТ!!
33 Билет
1. Комплексные изображения синусоидальных функций.
Временные и временные диаграммы просты и наглядны, но неудобны при расчётах большого количества гармонических колебаний, т.к. требуют геометрических построений при сложении векторов. Поэтому удобнее располагать вектор гармонического колебания на комплексной плоскости, тогда конечную точку этого вектора можно выразить некоторым комплексным числом, которое называют текущим комплексом гармонического колебания или комплексом мгновенного значения. Сам вектор колебания в этом случае называют символическим; в общем виде: где – полная фаза колебаний (рис.7).

Текущий комплекс – мгновенное текущее значение гармонического колебания, как любое комплексное число, может быть представлено в 3-х формах:
1)
алгебраическая:
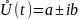 ;
;
где
а – действительная часть, проецируемая
на ось Оx;
b
– мнимая
часть,
проецируемая на ось Оy;
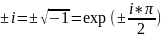 - мнимая единица.
- мнимая единица.
2)
тригонометрическая:
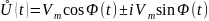 ,
,
где
модуль (амплитуда) –
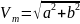 и фаза (аргумент) –
и фаза (аргумент) –
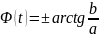 .
.
3)
показательная:
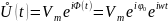 ,
,
где
 - комплексная амплитуда гармонического
колебания
– является основной характеристикой
при анализе цепей sin-тока,
т.к. информации об амплитуде и начальной
фазе при известной частоте w
достаточно для анализа частотных свойств
цепи. Поэтому
все методы анализа цепей при гармоническом
воздействии используют в качестве
переменных комплексные амплитуды тока
- комплексная амплитуда гармонического
колебания
– является основной характеристикой
при анализе цепей sin-тока,
т.к. информации об амплитуде и начальной
фазе при известной частоте w
достаточно для анализа частотных свойств
цепи. Поэтому
все методы анализа цепей при гармоническом
воздействии используют в качестве
переменных комплексные амплитуды тока
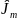 и напряжения
и напряжения
 ,
что составляет суть символического
метода анализа,
т.к. комплексная
амплитуда
есть начальное (при t=0)
значение символического вектора
гармонического колебания на комплексной
плоскости. При этом проекция символического
вектора на действительную ось Оx
– есть значение
,
что составляет суть символического
метода анализа,
т.к. комплексная
амплитуда
есть начальное (при t=0)
значение символического вектора
гармонического колебания на комплексной
плоскости. При этом проекция символического
вектора на действительную ось Оx
– есть значение
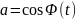 ;
а на мнимую ось Оу –
;
а на мнимую ось Оу –
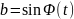 ;
т.е. мгновенные значения тока или
напряжения могут изменяться в зависимости
от выбранной проекции либо по cos,
либо по sin.
;
т.е. мгновенные значения тока или
напряжения могут изменяться в зависимости
от выбранной проекции либо по cos,
либо по sin.
Основные свойства текущего комплекса:
1.
Умножение на мнимую единицу:
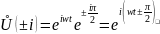 -
приводит к сдвигу фазы на
-
приводит к сдвигу фазы на
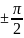 ,
т.е. к повороту символического вектора
на прямой угол.
,
т.е. к повороту символического вектора
на прямой угол.
2.
Производная от текущего комплекса:
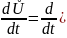
![]()
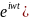 =
=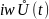 - равна произведению текущего комплекса
на
- равна произведению текущего комплекса
на
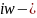 оператор дифференцирования в частотной
области.
оператор дифференцирования в частотной
области.
3.
Интеграл от текущего комплекса:

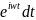 =
= равен умножению текущего комплекса на
равен умножению текущего комплекса на
 оператор интегрирования в частотной
области.
оператор интегрирования в частотной
области.
При
сложении и вычитании гармонических
колебаний удобнее использовать
алгебраическую форму записи, при
умножении и делении – показательную
форму. Аналогично мгновенным, текущие
комплексы можно ввести и для действующих
значений токов, напряжений и ЭДС: 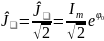
![]() ;
поскольку именно они чаще всего
используются при расчетах цепей
переменного тока.
;
поскольку именно они чаще всего
используются при расчетах цепей
переменного тока.
2. Дифференцирующие цепи.
Линейные
цепи часто используются для преобразования
формы импульсных колебаний. Рассмотрим
RC-цепь,
в которой выходным сигналом является
напряжение на резисторе. Ее дифференциальное
уравнение составляется следующим
образом: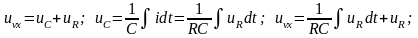
Продифференцировав
обе части по t
и домножив на RC,
получим окончательно: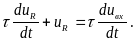
Если
постоянная времени
настолько мала, что duR/dt<<
uR
или τ=RC
<< 1 в любой момент времени, то первым
слагаемым в левой части (6.28) можно
пренебречь по сравнению со вторым, и
поэтому
 т.е. при выполнении вышеуказанного
условия RC-цепь
выполняет операцию приближенного
дифференцирования сигнала. Схемотехническое
применение дифференцирующих
цепей
– создание обострителей импульсных
сигналов.
т.е. при выполнении вышеуказанного
условия RC-цепь
выполняет операцию приближенного
дифференцирования сигнала. Схемотехническое
применение дифференцирующих
цепей
– создание обострителей импульсных
сигналов.
Коэффициент передачи рассматриваемой цепи K(jw) = jwRC / (1 + jwRC) будет действительно близок к частотному коэффициенту передачи идеального дифференциатора K(jw) jw, если произведение w пренебрежимо мало по сравнению с единицей в той области частот, где сосредоточена основная доля энергии сигнала. Так, если входной сигнал – прямоугольный видеоимпульс с длительностью и, то, используя грубую оценку для верхней граничной частоты в спектре импульса wb = 2/и, получаем условие, обеспечивающее пригодность RC-цепи для приближенного дифференцирования такого сигнала: = RС << и /(2).

С
