
- •1 Билет
- •1. Общая классификация сигналов.
- •2. Элементы цепей синусоидального тока. Резистор.
- •3. Интегрирующие цепи.
- •2 Билет
- •1. Импульсные сигналы.
- •2. Элементы цепей синусоидального тока. Конденсатор.
- •3. Преобразование Лапласа и его свойства.
- •1. Классификация сигналов по структуре и соответствующие им цепи.
- •2. Элементы цепей синусоидального тока. Катушка индуктивности.
- •3. Операторный метод анализа линейных стационарных систем.
- •4 Билет
- •1. Классификация цепей. Свойства линейных цепей с постоянными параметрами.
- •2. Общие комплексные сопротивления и проводимости цепей синусоидального тока.
- •3. Свойства передаточной функции. Формула обращения.
- •5 Билет
- •1. Свойства параметрических и нелинейных цепей. Этапы анализа цепей.
- •2. Последовательное соединение элементов цепи синусоидального тока.
- •3. Аналитические свойства входного сопротивления двухполюсника.
- •6 Билет
- •1. Элементы теории ортогональных сигналов.
- •2. Параллельное соединение элементов цепи синусоидального тока.
- •3. Синтез пассивных двухполюсников. Метод Фостера.
- •7 Билет
- •1. Связь обобщенного ряда Фурье и энергетических характеристик сигнала.
- •2. Резонанс напряжений.
- •3. Синтез пассивных двухполюсников. Метод Кауэра.
- •8 Билет
- •1. Гармонический анализ периодических сигналов.
- •2. Резонанс токов.
- •3. Четырехполюсники и их классификация.
- •9 Билет
- •1. Гармонический анализ непериодических сигналов. Преобразование Фурье.
- •2. Энергетический анализ цепей синусоидального тока.
- •3. Системы y и н параметров четырехполюсников.
- •10 Билет
- •1. Свойства преобразования Фурье. Сдвиг сигнала во времени и по частоте.
- •2. Согласование источника энергии с нагрузкой.
- •3. Системы z и а параметров.
- •11 Билет
- •1. Свойства преобразования Фурье. Изменение масштаба времени, дифференцирование и интегрирование колебаний.
- •2. Основные параметры цепей с индуктивно-связанными элементами.
- •3. Передаточная функция четырехполюсника и ее свойства.
- •12 Билет
- •1. Свойства преобразования Фурье. Сумма и произведение двух колебаний.
- •2. Индуктивная связь двух катушек.
- •3. Минимально-фазовые и неминимально-фазовые цепи. Коэффициент передачи мощности четырехполюсника.
- •13 Билет
- •1. Свойства преобразования Фурье. Взаимная заменяемость частоты и времени в преобразованиях Фурье.
- •2. Вариометры.
- •3. Фильтры и их общая классификация.
- •14 Билет
- •1. Распределение энергии в спектрах периодических сигналов.
- •2. Идеальный трансформатор.
- •3. Классификация фильтров по полосе пропускания.
- •15 Билет
- •1. Линейные цепи постоянного тока. Основные определения.
- •2. Элементы трехфазных систем. Симметричные и уравновешенные системы.
- •3. Алгоритм проектирования фильтров и допустимые пределы отклонения характеристик.
- •16 Билет
- •1. Элементы цепей постоянного тока. Резистор.
- •2. Соединение трехфазной системы звездой.
- •3. Фнч. Фильтр Баттерворта.
- •17 Билет
- •1. Элементы цепей постоянного тока. Катушка индуктивности.
- •2. Соединение трехфазной системы треугольником.
- •3. Фнч. Фильтр Чебышева.
- •18 Билет
- •1. Элементы цепей постоянного тока. Конденсатор.
- •2. Расчет симметричных режимов работы трехфазных систем.
- •3. Структурный синтез фнч.
- •19 Билет
- •1. Схемы замещения источников электрической энергии.
- •2. Расчет несимметричных режимов работы трехфазных систем.
- •3. Реализация фвч и пф.
- •20 Билет
- •1. Топологии цепей. Основные понятия.
- •2. Метод симметричных составляющих.
- •3. Передаточная функция системы с ос.
- •21 Билет
- •1. Топологии цепей. Матрицы соединений.
- •2. Свойства симметричных составляющих токов, напряжений и сопротивлений различных последовательностей трехфазных систем.
- •3. Устойчивость цепей с ос.
- •22 Билет
- •1. Законы Кирхгофа в линейных цепях.
- •2. Мощность трехфазных цепей.
- •3. Операционный усилитель.
- •23 Билет
- •1. Закон Ома для участка цепи с эдс.
- •2. Простейшие разрывные функции и их свойства.
- •3. Принцип построения активных rc-фильтров.
- •24 Билет
- •1. Правила делителей напряжения и тока.
- •2. Линейные стационарные системы и их математические модели.
- •3. Задача оптимальной фильтрации. Отношение сигнал/шум.
- •25 Билет
- •1. Эквивалентные преобразования линейных электрических цепей.
- •2. Импульсная характеристика линейной стационарной системы. Интеграл Дюамеля.
- •3. Критерий оптимальности линейного частотного фильтра.
- •26 Билет
- •1. Метод наложения.
- •2. Переходная характеристика линейной системы и ее связь с импульсной.
- •3. Согласованный линейный фильтр.
- •27 Билет
- •1. Метод эквивалентного генератора.
- •2. Частотный коэффициент передачи линейной стационарной системы.
- •3. Частотный коэффициент передачи согласованного фильтра.
- •28 Билет
- •1. Метод уравнений Кирхгофа.
- •2. Линейные динамические системы. Частотный коэффициент передачи линейной динамической системы.
- •3. Безынерционные нелинейные преобразования.
- •29 Билет
- •1. Метод контурных токов.
- •2. Законы коммутации в электрических цепях.
- •1 Закон коммутации:Ток в индуктивном элементе скачком измениться не может, т.Е. Ток до момента коммутации должен быть равен току в момент коммутации: .
- •3. Характеристики нелинейных элементов.
- •30 Билет
- •1. Метод узловых потенциалов.
- •2. Классический метод анализа переходных процессов.
- •3. Аппроксимация нелинейных характеристик.
- •31 Билет
- •1. Однофазные цепи синусоидального тока. Основные понятия.
- •2. Коэффициент передачи многокаскадных систем. Частотный коэффициент передачи мощности.
- •3. Воздействие гармонических колебаний на цепи с безынерционными нелинейными элементами.
- •32 Билет
- •1. Изображение синусоидальных функций в декартовой плоскости. Векторные диаграммы.
- •2. Спектральный метод анализа линейных стационарных систем.
- •3. Бигармоническое воздействие на нелинейные элементы.
- •33 Билет
- •1. Комплексные изображения синусоидальных функций.
- •2. Дифференцирующие цепи.
- •3. Классификация фильтров по полосе пропускания.
28 Билет
1. Метод уравнений Кирхгофа.
Для электрических цепей с большим число ветвей применение методов наложения и эквивалентных источников становится неэффективным. Универсальным методом анализа является использование законов Кирхгофа.
1-й закон Кирхгофа устанавливает взаимосвязь токов для любого узла. И поскольку в любой электрической цепи, состоящей из p-ветвей и q-узлов, число независимых узлов m=q-1, то число линейно независимых уравнений, составленных по 1-му закону Кирхгофа, также равно m.
2-ой закон Кирхгофа устанавливает взаимосвязь напряжений в любом контуре цепи. Число независимых контуров n=p–m будет определять число линейно независимых уравнений по второму закону Кирхгофа. Тогда общее число линейно независимых уравнений, составленных по двум законам Кирхгофа: p= m + n, то есть соответствует общему числу неизвестных токов во всех ветвях. При этом направления токов в ветвях и обхода контуров выбираются произвольно. Так, для мостовой схемы типа «конверт»: p = 6; q = 4; m = q – 1 = 3; n = p – m = 3; получим две системы уравнений:
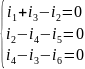
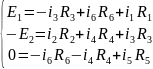
П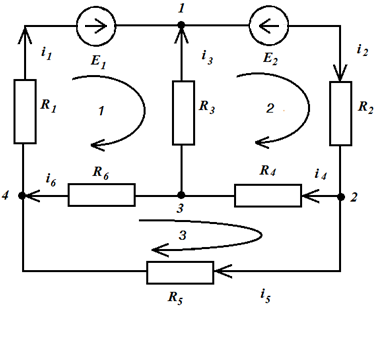 о
закону Ома для любой к-ветви:
о
закону Ома для любой к-ветви:
Uk = ikRk. Подставляя эти соотношения в получим 6 уравнений для токов, решив которые, можно определить токи и напряжения во всех ветвях. Так как решение системы из шести уравнений достаточно трудоемко, такие задачи удобнее выполнять на ЭВМ. Для этого полученное уравнение форматируют, то есть приводят к матричной форме.
Составим редуцированную матрицу соединений для узлов 1-3:
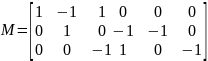
Тогда система уравнений (21) для токов в матричной форме примет вид:
 .
.
При этом наличие в активной линейной цепи источников тока учитывается как отдельные ветви в редуцированной матрице соединений и дополнительные строки в матрице-столбце токов.
Перепишем уравнения для напряжений в контурах из (21) в виде:
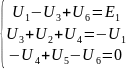
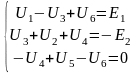 .
.
Для этой системы, аналогично редуцированной матрице соединений, можно записать матрицу контуров N, состоящей из n-строк по числу независимых контуров и p- столбцов по количеству ветвей; при этом на пересечении i-ой строки и j-го столбца будут находиться:
+1, если направление тока в j-ой ветви i-го контура совпадает с направлением обхода;
-1, если направления противоположны;
0, если j-я ветвь в этот контур не входит.
Если в j-ой ветви имеется источник ЭДС, то напряжение этой ветви:
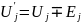 ,
причем знак «-» ставится при совпадении
направлений ЭДС источника и падения
напряжения ветви, а знак «+» при
противоположных направлениях. Так, в
данной схеме: для 1-го контура
,
причем знак «-» ставится при совпадении
направлений ЭДС источника и падения
напряжения ветви, а знак «+» при
противоположных направлениях. Так, в
данной схеме: для 1-го контура
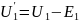 ;
для 2-го контура
;
для 2-го контура
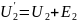 .
Тогда редуцированная матрица контуров
и соответствующая система уравнений
будут иметь вид:
.
Тогда редуцированная матрица контуров
и соответствующая система уравнений
будут иметь вид:
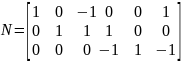 ;
;
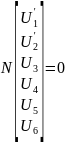 .
.
2. Линейные динамические системы. Частотный коэффициент передачи линейной динамической системы.
Линейными динамическими системами называются системы, обладающие следующим свойством: сигнал на их выходе определяется не только величиной входного сигнала в рассматриваемый момент времени, но и всей «предысторией» входного процесса. Иначе говоря, линейная динамическая система обладает некоторой памятью, от характера которой зависят все особенности преобразования входного сигнала.
Для этих систем связь между входными и выходными сигналами устанавливается с помощью дифференциального уравнения:
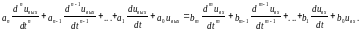
Именно такой оказывается динамическая связь между мгновенными значениями входного и выходного сигналов в электрической цепи с сосредоточенными параметрами. Если эта цепь линейна и стационарна, то все коэффициенты - постоянные вещественные числа.
Пусть
входной сигнал uвх(t)
задан. Тогда правая часть данного
уравнения, которую можно обозначить
f(t),
является известной функцией; и задача
анализа поведения системы сводится к
проблеме решения линейного дифференциального
уравнения n-го
порядка с постоянными коэффициентами
(более подробно об этом в классическом
методе анализа):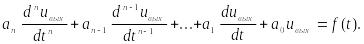
Порядок этого уравнения принято называть порядком динамической системы.
Частотный
коэффициент передачи линейной динамической
системы.
Если на вход линейной динамической
системы поступает экспоненциальный
сигнал вида uвх(t)
= exp(jwt),
то сигнал на выходе uвых(t)=K(jw)exp(jwt).
Подставляя эти выражения в исходное
дифференциальное уравнение (6.13), после
сокращения на общий экспоненциальный
множитель можно определить частотный
коэффициент передачи системы: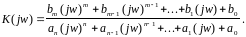
Итак, частотный коэффициент передачи любой динамической системы, описываемой обыкновенными дифференциальными уравнениями с постоянными коэффициентами, представляет собой дробно-рациональную функцию переменной jw; коэффициенты этой функции совпадают с коэффициентами дифференциального уравнения.
