3.8.4. Определение радиуса ролика

При проектировании кулачкового механизма с роликом значение R_P радиуса ролика может быть задано конструктором. В этом случае необходима проверка правильности выбранной величины. Если R_P не задано, то эта величина рассчитывается на основе анализа кривизны профиля кулачка. Для неё должны удовлетворяться следующие неравенства [1, 9, 14]:

R_P  0,7 _min; R_P  0,4 R _O; (3.40)

где _min – минимальный радиус кривизны центрового профиля кулачка;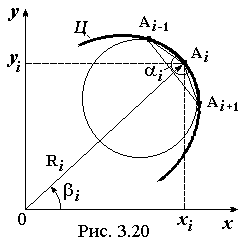

R_O – радиус базовой окружности кулачка.

В п. 3.8.1, 3.8.3 рассмотрен расчет координат профиля кулачка (R_i, _i), i = 1,2 … n. По этим величинам для каждых трех точек на центровом профиле кулачка A_i-1, A_i, A_i+1 (рис. 3.20) можно определить радиус описанной окружности _i, который и будет приближенным значением радиуса кривизны центрового профиля в i-й точке.

x_i = R_i cos _i; y_i = R_i sin _i. ( 3.41 )

Длины сторон треугольника A_i-1A_iA_i+1:

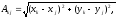
( 3.42 )

где k, j = i–1, i, i+1.

Решая треугольник A_i-1A_iA_i+1, получаем:

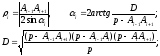
( 3.43 )

где p – полупериметр треугольника A_i-1A_iA_i+1.

Произведя вычисления по формулам (3.41) … (3.43) для i = 2, 3 … n-1, находим значение

_min = min _i.

Если R_P задан конструктором, то проверяются условия (3.40). Если он не задан или эти условия не выполняются, то конструктор, по известному теперь _min из конструктивных соображений может принять любое значение R_P в соответствии с условиями (3.40).

4. Зубчатые механизмы

4.1. Классификация Зубчатые – это, наверное, самый широко распространенный класс механизмов. Большое разнообразие этих механизмов можно классифицировать следующим образом.

1. По структуре и кинематике:

а) механизмы с неподвижными осями колес (рис. 4.1а,в,г,д,е,ж);

б) механизмы, в составе которых есть колеса с подвижными осями: планетарные (рис. 4.1б) и дифференциальные;

в) механизмы, в составе которых есть упруго деформируемые колеса (волновые).

2. По расположению осей колес:

а) механизмы с параллельными осями колес (цилиндрические рис. 4.1а,д,е,ж);

б) оси колес пересекаются (конические – рис. 4.1в);

в) оси колес скрещиваются (винтовые – рис. 4.1г, червячные, гипоидные).

3. По форме рабочей поверхности зуба:

а) эвольвентные;

б) циклоидальные;

в) часовое зацепление (приближенное на основе циклоидального);

г) зацепление Новикова;

д) цевочное зацепление.

4. По форме оси зуба: а) прямозубые (рис. 4.1д);

б) косозубые (рис. 4.1е);

в) шевронные (рис. 4.1ж);

г) винтовые (рис. 4.1г).

4.2. Основная теорема зацепления

Основная теорема зацепления или теорема Виллиса формулируется следующим образом (рис. 4.2а). Общая нормаль к поверхностям двух вращающихся тел, проведенная в точке контакта отсекает от межцентрового расстояния отрезки, обратно пропорциональные угловым скоростям звеньев. То есть:

Доказательство. Пусть k – точка контакта, w – точка пересечения общей нормали n-n с линией межцентрового расстояния O₁O₂. Построим план скоростей v_К1 – скорость точки k, если считать её принадлежащей звену 1, v_К2 – скорость точки k, если считать её принадлежащей звену 2 (см. рис. 4.2а). Условием непрерывности контакта является равенство проекций этих скоростей на общую нормаль n-n: v_К1ⁿ = v_К2ⁿ.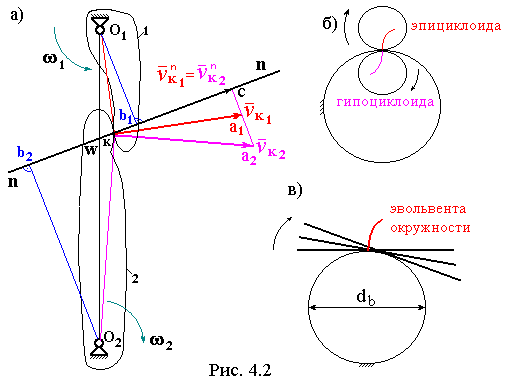

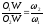
Угловые скорости звеньев:

Из подобия треугольников: O₁b₁k  ka₁С и O₂b₂k  ka₂С:

Тогда отношение угловых скоростей:

( 5.1 )

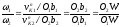
Последнее равенство в соотношениях (4.1) следует из подобия треугольников: O₁b₁W  O₂b₂W (см. рис. 4.2а). Теорема доказана.

Когда в процессе движения точка k проходит положение w, то в этот момент равны, не только нормальные, но и касательные составляющие скорости v_К1^ = v_К2^, т.е. скорости полностью равны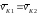, поэтому точкаw названа полюсом зацепления.

По определению, отношение угловых скоростей называется передаточным отношением: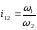

Как правило, при проектировании зубчатых механизмов требуется постоянное передаточное отношение.

Следствия из основной теоремы зацепления. Для того чтобы передаточное отношение было постоянным необходимо, чтобы в процессе зацепления полюс зацепления не менял своего положения.

В свою очередь для того, чтобы полюс зацепления не менял своего положения необходимо, чтобы профили контактирующих поверхностей представляли собой взаимоогибаемые кривые.

В полной мере этому требованию удовлетворяют циклоиды (см. рис. 4.2б), которые образуются при перекатывании без скольжения одной окружности по другой. И исторически первым правильным зацеплением было именно циклоидальное, т.е. такое, когда боковые поверхности зубьев представляют собой отрезки циклоид.

Однако у циклоидального зацепления есть недостаток – его сравнительно высокая стоимость. Причины этого рассматриваются позже в подразделе “Методы изготовления зубчатых колес”.

Требованию основной теоремы зацепления удовлетворяет и эвольвента окружности – кривая, образующаяся при перекатывании без скольжения прямой по окружности (см. рис. 4.2в). Изготовление колес с эвольвентным профилем зубьев оказалось гораздо более дешевым, и, несмотря на то, что такие колеса имеют несколько большие размеры, – эвольвентное зацепление в машиностроении получило самое широкое применение. В дальнейшем рассматривается именно этот вид зацепления.