
- •Балтийский государственный технический университет «военмех» им. Д.Ф. Устинова
- •В.Ю. Лавров Введение в теорию механизмов и машин Учебное пособие
- •Содержание
- •Введение
- •1. Структурный анализ и синтез рычажных механизмов
- •1.1. Основные определения
- •1.2. Число степеней свободы механизма
- •1.3. Структурные группы
- •1.4. Структурный синтез механизмов с помощью групп Ассура
- •1.5. Диагностика наличия пассивных связей
- •1.6. Элементы метрического синтеза рычажных механизмов
- •Математически это можно выразить следующим образом. Если выполняются условия:
- •Если выполняются условия:
- •2. Кинематический анализ рычажных механизмов
- •2.1. Постановка задачи
- •2.2. Кинематика входных механизмов
- •2.2.1. Кривошип
- •2.2.2. Ползун
- •2.2.3. Качающийся ползун
- •2.3. Аналитические зависимости кинематического анализа для структурных групп, связанных со стойкой
- •2.3.1. Трёхшарнирная структурная группа
- •2.3.2. Структурная группа "шатун - ползун"
- •Уравнение замкнутого векторного контура:
- •2.3.3. Кулисные структурные группы
- •2.3.4. Структурная группа "шарнир – ползун – ползун"
- •2.3.5. Структурная группа "ползун – шарнир – ползун"
- •2.4. Метод преобразования координат
- •2.5. Общая последовательность кинематического анализа
- •2.6. Передаточные функции, передаточное отношение
- •2.6.1. Передаточная функция
- •2.6.2. Передаточное отношение
- •2.7. Графо-аналитический метод планов2
- •3. Кулачковые механизмы
- •3.1. Классификация
- •3.2. Основные геометрические параметры кулачковых механизмов
- •3.3. Фазы работы кулачковых механизмов. Фазовые и конструктивные углы
- •3.4. Выбор закона движения выходного звена
- •3.4.1. Позиционные механизмы
- •3.4.2. Функциональные механизмы
- •3.5. Угол давления в кулачковых механизмах
- •3.6. Связь между углом давления и основными геометрическими параметрами кулачкового механизма
- •3.6.1. Механизм с толкателем центрального типа
- •Для надежного определения rOmin по формуле (3.7) rOmin I должны быть вычислены с достаточно мелким шагом по углу поворота кулачка.
- •3.6.2. Механизм с толкателем при наличии эксцентриситета
- •3.7. Определение основных геометрических параметров
- •3.7.1. Механизмы с толкателем и роликом или с заостренным толкателем
- •3.7.2. Механизмы с плоским толкателем
- •3.7.3. Механизмы с коромыслом и роликом
- •3.7.4. Механизмы с плоским коромыслом
- •3.8. Расчет профиля кулачка
- •3.8.1. Механизмы с толкателем и роликом или с заостренным толкателем
- •3.8.2. Механизмы с плоским толкателем
- •3.8.3. Механизмы с коромыслом и роликом
- •3.8.4. Определение радиуса ролика
- •4. Зубчатые механизмы
- •4.1. Классификация Зубчатые – это, наверное, самый широко распространенный класс механизмов. Большое разнообразие этих механизмов можно классифицировать следующим образом.
- •4.2. Основная теорема зацепления
- •4.3. Основные параметры эвольвентного зацепления
- •4.4. Теоретический и рабочий участок линии зацепления, зоны одно- и двупарного зацепления, коэффициент перекрытия
- •4.5. Методы изготовления зубчатых колес
- •4.5.2. Метод обкатки
- •Тогда ( 4.11 )
- •4.7.2.2. Гиперболоидные зубчатые передачи
- •Винтовая передача
- •Червячная передача
- •4.8. Кинематический анализ зубчатых механизмов
- •4.8.1. Рядные механизмы
- •4.8.2. Механизмы с промежуточными колесами
- •4.8.3. Планетарные зубчатые механизмы
- •4.8.4. Волновые зубчатые механизмы
- •4.8.5. Определение передаточных отношений сложных зубчатых механизмов
- •4.9. Силовой расчет зубчатых механизмов
- •4.9.1. Расчет крутящих моментов на валах
- •4.9.2. Усилия в зацеплениях
- •4.9.3. Определение реакций в опорах валов
- •4.10. Кпд зубчатых механизмов
- •4.10.1. Кпд зубчатых механизмов с неподвижными осями колес
- •4.10.2. Кпд планетарных зубчатых механизмов
- •4.11. Дифференциальные зубчатые механизмы
- •5. Силовой расчет рычажных механизмов
- •5.1. Постановка задачи
- •5.2. Общий порядок силового расчета
- •5.3. Внешние силы
- •5.4. Определение реакций в кинематических парах структурных групп
- •5.4.1. Аналитическое решение
- •5.4.1.1. Трёхшарнирная структурная группа
- •5.4.1.2. Структурная группа "шатун – ползун"
- •5.4.1.3. Кулисные структурные группы
- •5.4.1.4. Структурная группа типа "шарнир – ползун – ползун"
- •5.4.1.5. Структурная группа "ползун – шарнир – ползун"
- •5.4.2. Графо-аналитическое решение задачи силового расчёта
- •5.5. Силовой расчет кривошипа
- •5.5.1. Одноколенный кривошип
- •5.5.1.1. Силовой расчет кривошипа при передаче крутящего момента
- •5.5.1.2. Силовой расчет кривошипа при передаче крутящего момента
- •5.5.2. Двухколенный кривошип
- •5.5.2.1. Крутящий момент на кривошип передаётся через зубчатую или фрикционную пару
- •5.5.2.2. Крутящий момент на кривошип передается через планетарный или волновой механизм
- •6. Уравновешивание механизмов
- •6.1. Постановка задач
- •6.2. Уравновешивание роторов
- •6.2.1. Уравновешивание роторов при известном расположении неуравновешенных масс
- •6.2.2. Уравновешивание роторов при неизвестном расположении неуравновешенных масс
- •Производят второй разгон ротора, дают выбег и замеряют амплитуду резонансных колебаний. Обозначим ее: a1.
- •7.2. Метод приведения
- •7.3. Приведение сил и моментов
- •7.4. Приведение масс и моментов инерции
- •7.5. Уравнение движения
- •7.6. Анализ уравнения движения
2.7. Графо-аналитический метод планов2
Этот
метод кинематического анализа более
нагляден, чем метод векторных контуров
и преобразования координат и особенно
полезен для изучения механики механизмов
и удобен для проверочных расчётов. Уже
из его названия следует, что это
комбированный метод. Его
суть состоит
в том, что аналитически формируются
кинематические уравнения, которые
решаются с применением графических
построений, называемых планами скоростей
и ускорений.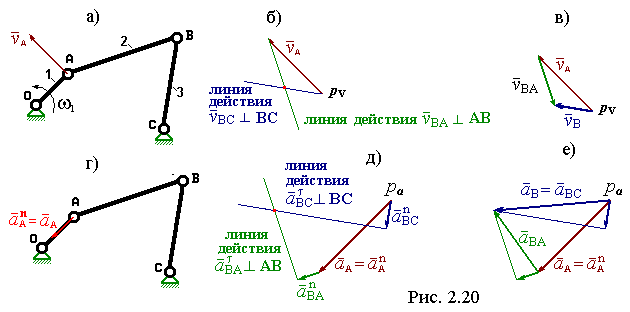
Схема для расчёта этим методом кинематики четырёхшарнирного механизма представлена на рис. 2.20.
Построение плана скоростей четырёхшарнирного механизма
1. Выбранном масштабе вычерчиваем план механизма в расчётном положении (см. рис. 2.20а).
2. Параметры движения входного кривошипа OA известны по постановке задачи, вычисляем величину скорости конца кривошипа
vA=1l1
3.
Полагая, что кривошип является абсолютно
твёрдым телом, направляем вектор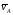 перпендикулярно оси кривошипа (см. рис.2.20а).
перпендикулярно оси кривошипа (см. рис.2.20а).
Определим скорость шарнира B
Он принадлежит одновременно шатуну AB и коромыслу BC. (.)B AB, поэтому, если принять (.)A за полюс, то скорость (.)B представима как
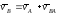
где
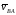 –
скорость (.)B
относительно (.)A.
–
скорость (.)B
относительно (.)A.
С другой стороны, (.)B BC. Тогда скорость точки B представима как
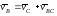
где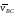 – скорость (.)B
относительно (.)C.
– скорость (.)B
относительно (.)C.
В
данном случае vC
= 0, поэтому .
.
Таким
образом, для определения
 мы
получили систему векторных уравнений:
мы
получили систему векторных уравнений: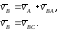
( 2.38 )
Решим её графически путём построения плана скоростей, который представляет собой графическое представление системы (2.38).
1.
Выбираем масштабный коэффициент для
плана скоростей kV,
имеющий размерность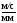 ,и из полюса плана
pV
в этом масштабе откладываем вектор
,и из полюса плана
pV
в этом масштабе откладываем вектор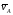 (см. рис. 2.20б).
(см. рис. 2.20б).
2.
Величина вектора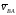 нам пока не известна, но известно, что
его линия действия перпендикулярна оси
шатунаAB.
В соответствии с первым уравнением
системы (2.38) проводим её на плане скоростей
из конца вектора
нам пока не известна, но известно, что
его линия действия перпендикулярна оси
шатунаAB.
В соответствии с первым уравнением
системы (2.38) проводим её на плане скоростей
из конца вектора
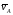 перпендикулярно
шатунуAB
– зелёная линия на рис. 2.20б.
перпендикулярно
шатунуAB
– зелёная линия на рис. 2.20б.
3.
Величина вектора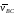 пока тоже не известна, но известно, что
её линия действия перпендикулярна оси
коромыслаBC.
Проводим её на плане скоростей из его
полюса, т.к. первое слагаемое в правой
части второго уравнения системы (2.38)
равно нулю (синяя линия перпендикулярно
BC)
– рис. 2.20б.
пока тоже не известна, но известно, что
её линия действия перпендикулярна оси
коромыслаBC.
Проводим её на плане скоростей из его
полюса, т.к. первое слагаемое в правой
части второго уравнения системы (2.38)
равно нулю (синяя линия перпендикулярно
BC)
– рис. 2.20б.
4. Точка пересечения этих линий удовлетворяет обоим уравнениям системы (2.38). Следовательно, она и является её решением. Обозначаем найденные векторы – рис. 2.20в.
Величины найденных векторов определим, измеряя их на плане и умножая на масштабный коэффициент.
Величины угловых скоростей: 2 = vBA/lAB, 3 = vB/lBC.
Построение плана ускорений четырёхшарнирного механизма
при постоянной угловой скорости кривошипа
1. Выбранном масштабе вычерчиваем план механизма в расчётном положении (см. рис. 2.20а,г).
2. Параметры движения входного кривошипа OA известны по постановке задачи, вычисляем величину ускорения конца кривошипа, которая при 1 = Const имеет только нормальную составляющую
aA=aAn=12l1
3.
Полагая, что кривошип является абсолютно
твёрдым телом, направляем вектор
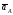 вдоль оси кривошипа от (.)A
к (.)O
(см. рис. 2.20г).
вдоль оси кривошипа от (.)A
к (.)O
(см. рис. 2.20г).
Определим ускорение шарнира B
Он принадлежит одновременно шатуну AB и коромыслу BC.
(.)B
AB,
поэтому, если принять (.)A
за полюс, то ускорение (.)B
представимо как
где
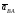 –
ускорение (.)B
относительно (.)A,
–
ускорение (.)B
относительно (.)A,
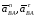 – его нормальная и касательная
составляющие.
– его нормальная и касательная
составляющие.
С другой стороны, (.)B BC. Тогда ускорение точки B представима как
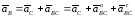
где
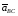 –
ускорение (.)B
относительно (.)С,
–
ускорение (.)B
относительно (.)С,
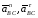 – его нормальная и касательная
составляющие.
– его нормальная и касательная
составляющие.
В
данном случае aC
= 0, поэтому
 .
.
Таким
образом, для определения
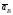 мы получили систему векторных уравнений:
мы получили систему векторных уравнений:
(2.39)
Решим её графически путём построения плана ускорений. План ускорений представляет собой графическое представление системы (2.39).
1.
Выбираем масштабный коэффициент для
плана ускорений ka,
имеющий размерность
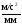 ,
и из полюса планаpa
в этом
масштабе откладываем вектор
,
и из полюса планаpa
в этом
масштабе откладываем вектор
 (см.
рис.2.20д).
(см.
рис.2.20д).
2. Величину нормальной составляющей aBAn можно вычислить:
aBAn = vBA2/ l2 = 22 l2.
Направлено она вдоль оси шатуна 2 от (.)B к (.)A. Откладываем её на плане (см. рис. 2.20д).
3. Касательная составляющая aBA нам пока не известна, но известно, что её линия действия перпендикулярна оси шатуна AB. В соответствии с первым уравнением системы (2.39) проводим её на плане скоростей из конца вектора aBAn перпендикулярно шатуну AB – тонкая зелёная линия на рис. 2.20д.
4. Величину нормальной составляющей aBCn можно вычислить:
aBCn = vB2/ l3 = 32 l3.
Направлена она вдоль оси коромысла 3 от (.)B к (.)C. Откладываем её на плане ускорений из его полюса, т.к. первое слагаемое в правой части второго уравнения системы (2.39) равно нулю (см. рис. 2.20д).
5. Касательная составляющая aBC пока тоже не известна, но известно, что её линия действия перпендикулярна оси коромысла BC. Проводим её на плане ускорений из конца вектора aBCn – тонкая синяя линия на рис. 2.20д.
6. Точка пересечения линий удовлетворяет обоим уравнениям системы (5.13). Следовательно, она и является её решением. Обозначаем найденные векторы – рис. 2.20е.
Векторные суммы нормальных и касательных составляющих являются полными ускорениями точек
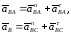
Величины найденных векторов определим, измеряя их на плане и умножая на масштабный коэффициент.
Величины угловых ускорений: 2 = aBA/lAB, 3 = aBC/lBC.
