3.3. Фазы работы кулачковых механизмов. Фазовые и конструктивные углы

Кулачковые механизмы могут реализовывать на выходном звене законы движения практически любой сложности. Но любой закон движения может быть представлен комбинацией следующих фаз:

1. Фаза удаления. Процесс перемещения выходного звена (толкателя или коромысла), когда точка контакта кулачка и толкателя удаляется от центра вращения кулачка.

2. Фаза возврата (приближения). Процесс перемещения выходного звена, когда точка контакта кулачка и толкателя приближается к центру вращения кулачка.

3. Фазы выстоя. Ситуация, когда при вращающемся кулачке точка контакта кулачка и толкателя неподвижна. При этом различают, фазу ближнего выстоя – когда точка контакта находится в самом ближнем положении к центру кулачка, фазу дальнего выстоя – когда точка контакта находится в самом дальнем положении от центра кулачка и фазы промежуточных выстоев. Фазы выстоя имеют место, когда точка контакта движется по участку профиля кулачка, имеющего форму дуги окружности, проведенной из центра вращения кулачка.

Приведенная классификация фаз в первую очередь относится к позиционным механизмам.

Каждой фазе работы соответствует свой фазовый угол работы механизма и конструктивный угол кулачка.

Фазовым углом называется угол, на который должен повернуться кулачок, для того, чтобы полностью прошла соответствующая фаза работы. Эти углы обозначаются буквой  с индексом, указывающим тип фазы, например, _У – фазовый угол удаления, _Д – фазовый угол дальнего выстоя, _В – фазовый угол возврата, _Б – фазовый угол ближнего выстоя.

Конструктивные углы кулачка определяют его профиль. Они обозначаются буквой  с такими же индексами. На рис. 3.2а показаны эти углы. Они ограничены лучами, проведенными из центра вращения кулачка в точки на его центровом профиле, в которых меняется профиль кулачка при переходе от одной фазы к другой.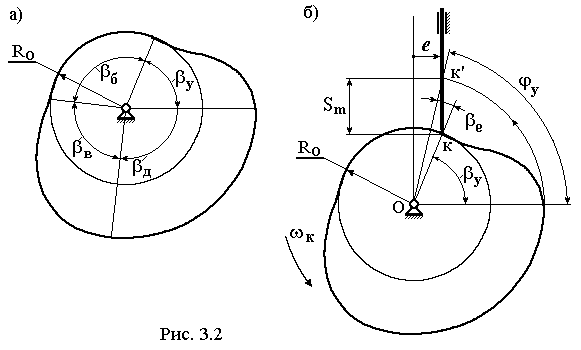

На первый взгляд может показаться, что фазовые и конструктивные углы равны. Покажем, что это не всегда так. Для этого выполним построение, показанное на рис. 3.2б. Здесь механизм с толкателем при наличии у него эксцентриситета установлен в положение, соответствующее началу фазы удаления; к – точка контакта кулачка и толкателя. Точка к’ – это положение точки к, соответствующее окончанию фазы удаления. По построению видно, что для того чтобы точка к заняла положение к’ кулачок должен повернуться на угол _У, не равный _У, а отличающийся на угол е, называемый углом эксцентриситета. Для механизмов с толкателем можно записать соотношения:

_У = _У + е, _В = _В – е,

_Д = _Д , _Б = _Б

3.4. Выбор закона движения выходного звена

Методика выбора закона движения выходного звена зависит от назначения механизма. Как уже отмечалось, по назначению кулачковые механизмы подразделяют на две категории: позиционные и функциональные.

3.4.1. Позиционные механизмы

Для наглядности рассмотрим самый простой случай двухпозиционного механизма, который просто “перебрасывает” выходное звено из одного крайнего положения в другое и обратно.

На рис. 3.3 показан закон движения – график перемещения толкателя такого механизма, когда весь процесс работы представляется комбинацией четырех ваз: удаление, дальний выстой, возврат и ближний выстой. Здесь  – угол поворота кулачка, и соответствующие фазовые углы обозначены: _у, _д, _в, _б. По оси ординат отложено перемещение выходного звена: для механизмов с коромыслом это  – угол его поворота, для механизмов с толкателем S – перемещение толкателя.

В данном случае выбор закона движения состоит в определении характера движения выходного звена на фазах удаления и возврата. На рис. 3.3 для этих участков изображена какая-то кривая, но именно её и надо определить. Какие же критерии закладываются в основу решения этой задачи?

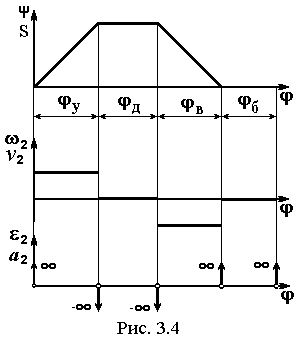
Пойдем от противного. Попробуем поступить “просто”. Зададим на участках удаления и возврата линейный закон перемещения. На рис. 3.4 показано к чему это приведет. Дважды дифференцируя функцию () или S() получаем, что на границах фаз будут возникать теоретически бесконечные, т.е. непредсказуемые ускорения, а, следовательно, и инерционные нагрузки. Это недопустимое явление получило название жесткого фазового удара.

Во избежание этого выбор закона движения производят исходя из графика ускорения выходного звена. На рис. 3.5 приведен пример. Задаются желаемой формой графика ускорения и его интегрированием находят функции скорости и перемещения.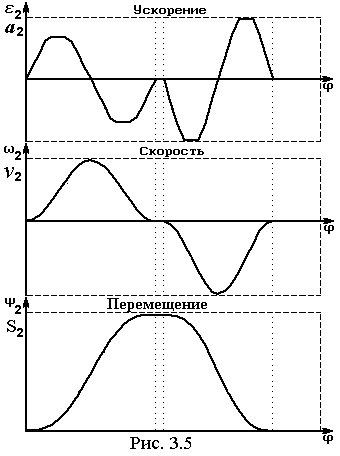

Зависимость ускорения выходного звена на фазах удаления и возврата обычно выбирают безударной, т.е. в виде непрерывной функции без скачков ускорения. Но иногда для тихоходных механизмов с целью уменьшения габаритов допускают явление мягкого удара, когда на графике ускорения наблюдаются скачки, но на конечную, предсказуемую величину.

На рис. 3.6 представлены примеры наиболее часто примеряемых видов законов изменения ускорения. Функции изображены для фазы удаления, на фазе возврата они аналогичны, но зеркально отражены. На рис. 3.6 представлены симметричные законы, когда ₁ = ₂ и характер кривых на этих участках одинаков. При необходимости применяют и несимметричные законы, когда ₁  ₂ или характер кривых на этих участках различен или и то и другое.

Выбор конкретного вида зависит от условий работы механизма, например, закон 3.6д применяют тогда, когда на фазе удаления (возврата) нужен участок с постоянной скоростью выходного звена.

Как правило, функции законов ускорения имеют аналитические выражения, в частности 3.6,а,д – отрезки синусоиды, 3.6,б,в,ж – отрезки прямых, 3.6,е – косинусоида, поэтому их интегрирование с целью получения скорости и перемещения не представляет трудностей. Однако заранее не известны амплитудные значения ускорения, но значение перемещения выходного звена на фазах удаления и возврата известны. Рассмотрим, как при этом найти и амплитуду ускорения и все функции, характеризующие движение выходного звена.

При постоянной угловой скорости вращения кулачка, когда угол его поворота и время связаны выражением  = t функции можно рассматривать как от времени, так и от угла поворота. Будем рассматривать их во времени и применительно к механизму с коромыслом.

На начальном этапе форму графика ускорения зададим в виде нормированной, то есть с единичной амплитудой, функции *(t). Для зависимости на рис. 3.6а это будет *(t) = sin(2t/T), где Т – время прохождения механизмом фазы удаления или возврата. Реальное ускорение выходного звена:

₂ (t) = _m *(t), (3.1)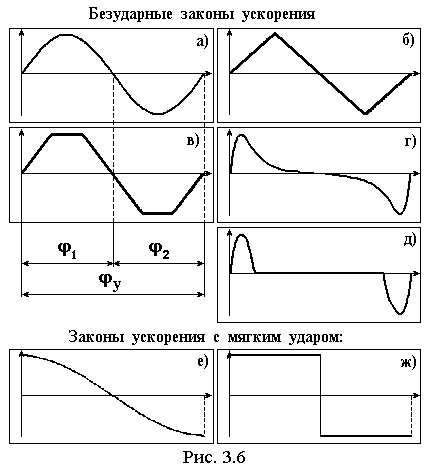

где _m – неизвестная пока амплитуда.

Дважды интегрируя выражение (3.1), получим:

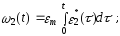
( 3.2 )

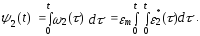
Интегрирование производится с начальными условиями: для фазы удаления ₂(t) = 0, ₂(t) = 0; для фазы возврата ₂(t) = 0, ₂(t) = _m. Требуемое максимальное перемещение выходного звена _m известно, поэтому амплитуда ускорения

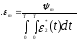
(3.3)

Каждому значению функций ₂(t), ₂(t), ₂(t) могут быть поставлены в соответствие величины ₂(), ₂(), ₂(), которые и используются для проектирования механизма, как это описано ниже.

Следует заметить, что существует и другая причина возникновения ударов в кулачковых механизмах, связанная с динамикой их работы. Кулачок может быть спроектирован и безударным, в том смысле, какой мы вкладывали в это понятие выше. Но на больших скоростях у механизмов с силовым замыканием возможен отрыв толкателя (коромысла) от кулачка. Через какое-то время замыкающая сила восстанавливает контакт, но это восстановление и происходит с ударом. Такие явления могут возникать, например, когда фаза возврата задана слишком маленькой. Профиль кулачка тогда на этой фазе получается крутым и по окончании фазы дальнего выстоя замыкающая сила не успевает обеспечить контакт и толкатель как бы срывается с профиля кулачка на дальнем выстое и может даже сразу ударить в какую-то точку кулачка на ближнем выстое. У механизмов с геометрическим замыканием ролик движется по пазу в кулачке. Поскольку между роликом и стенками паза обязательно есть зазор, то в процессе работы ролик ударяется о стенки, интенсивность этих ударов тоже возрастает с увеличением скорости вращения кулачка. Для изучения этих явлений необходимо составлять математическую модель работы всего механизма, но эти вопросы выходят за рамки данного курса.