Плотность распределения

Для СВ Х, с равной вероятностью принимающей любое значение из отрезка [0; 1], естественно считать, что вероятность попадания в отрезок [a; b]равна длине этого отрезка.

Пусть имеется СВ Х и неотрицательная функция f(х) такая, что для любых чисел а и b, , выполняется равенство:

.

В этом случае говорят, что СВ Х имеет плотность распределения f(х).

Записывается это выражение следующим образом:

.

Сходство и различия между законом распределения и плотностью распределения

Плотность вероятности непрерывной случайной величины (она же дифференциальная функция распределения вероятностей) - аналог закона распределения дискретной СВ. Между тем, имеются и сходство и различия.

1. Если закон распределения дискретной СВ графически изображается в виде отдельных точек плоскости, для наглядности соединённых ломаной линией (многоугольник распределения, полигон), то плотность вероятностей графически представляет собой непрерывную гладкую или кусочно-гладкую линию, если на разных отрезках задаётся разными функциями.

2. Аналитически плотность распределения задаётся формулой. Также как и непрерывная СВ, дискретная СВ может быть задана законом распределения аналитически.

3. Если закон распределения дискретной СВ ставит каждому значению x СВ Х в соответствие определённую вероятность. Считается, что для каждого отдельного (одиночного) значения непрерывной СВ вероятность равна нулю. Для непрерывных СВ можно найти только вероятность попадания в какой-либо интервал.

И графически вероятность попадания в интервал выражается площадью фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков – линиями, параллельными оси ординат, проходящими через концевые точки рассматриваемого интервала.

Свойства плотности вероятности

1) Значения плотности вероятности, т.е. значения функции f(x), неотрицательны: f(x) ≥ 0.

Для случайных событий было аналогично определено: .

2) Основное свойство плотности вероятности: интеграл (и собственный и/или несобственный) от плотности вероятности по всей области возможных значений СВ равен 1:

=1;

Геометрически это выражается тем, что площадь фигуры, ограниченной сверху графиком плотности вероятности, снизу - осью OX, равна 1.

Аналог для случайных событий:

Нормальный закон распределения

Особый интерес для практики представляет непрерывная случайная величина, имеющая так называемый нормальный закон распределения.

Нормальное распределение является хорошей моделью для реальных явлений, в которых:

1) имеется сильная тенденция данных группироваться вокруг центра;

2) положительные и отрицательные отклонения данных «от центра» (среднего значения) равновероятны;

3) при увеличении отклонения от центра, частота таких отклонений быстро уменьшается.

Нормальное распределение обладает рядом математических свойств, во многом обеспечивших его широкое применение в статистике.

Нормальное распределение зависит от двух параметров ии задаетсяфункцией плотности вида

,

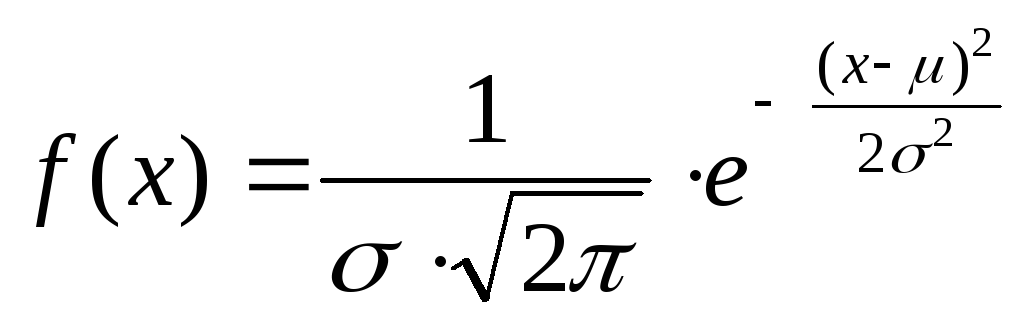где и- параметры распределения.

Случайную величину, распределённую нормально с параметрами и, будем обозначатьN(;).

Параметры иимеют вполне ясный смысл: это соответственно математическое ожиданиеМХ и стандартное отклонение случайной величины , распределенной по нормальному закону:

; .

Приведем некоторые факты относительно нормального распределения.

а). Среднее значение определяет меру расположения плотности.

б). Плотность нормального распределения симметрична относительно среднего.

в). Мода и медиана нормального распределения соответственно равны:Mо=, Mе=, где.

Изменение параметра нормального распределения DX приводит к «деформации» формы кривой по оси Ох, но в любом случае всегда площадь под кривой плотности вероятности неизменна и равна 1.

г). При увеличении дисперсии плотность нормального распределения «расплывается» или «растекается» вдоль осиОх. Другими словами: при неизменном математическом ожидании, чем больше, тем график более «пологий».

д). При уменьшении дисперсии плотность нормального распределения, наоборот, «сжимается», концентрируясь вокруг одной точки - точки максимального значения, совпадающей со средним значением.

е). В предельном случае нулевой дисперсии случайная величина «вырождается» и принимает единственное значение, равное среднему.

ж). Изменение второго параметра нормального распределения - МХ (m_x)- приводит к сдвигу кривой по оси Ох. При этом, при одинаковой дисперсии σ_x, чем больше МХ, тем «правее» расположен график.

Распределение с = 0 и= 1 называетсястандартным нормальным распределением, и оно обозначается N(0; 1).

Плотность стандартного нормального распределения будем обозначать особым образом, не f(x), а . Эту функцию называютфункцией Гаусса. Саму стандартную СВ обозначают – U.

Стандартная случайная величина определяется своей плотностью ,

.

График функции Гаусса называетсякривой вероятностей или Гауссианой.