4.2.7. Дифференциальные функции распределения по крупности

Дифференциальные функции распределения по крупности показывают число зерен или массовый выход каждого класса крупности в данном материале. Материал, состоящий из смеси зерен разных размеров, разделенный на классы крупности, можно рассматривать как статистический коллектив. Размер зерен будет аргументом коллектива, а общее число зерен в пробе материала или ее общая масса составят числовой или массовый объем статистического коллектива. Число зерен в каждом классе, или их массу, называют численностью класса, частотой или абсолютной частостью, а частоты классов, отнесенные к объему коллектива, - относительными частостями классов.

Если в прямоугольных координатах по оси абсцисс отложить крупность классов и на соответствующих интервалах крупности построить прямоугольники, площади которых будут пропорциональны частоте класса, то получим гистограмму распределения зерен материала. Это равнозначно построению прямоугольников высотой, равной частости на единицу длины интервала, на интервале как основании прямоугольника. При уменьшающемся интервале ступенчатая линия, сверху ограничивающая прямоугольники, приближается к плавной кривой; в пределе она дает дифференциальную функцию распределения (рис. 4.14, е). Ординаты функции распределения γ(х) выражают частость на единицу длины бесконечно узкого интервала по оси абсцисс, а площадь под кривой определяет число объектов (число зерен, массовый выход их) в соответствующих промежутках.

Зерна, диаметры которых меньше х_п и больше х_п1, образуют n-й класс - x_n + х_п-1 с интервалом крупности Δх_п = х_п  х_п1. Если число зерен в этом классе N_n, а масса их W_n, то относительная частость по числу зерен будет N_n / n и по массе W_n / W, где N - общее число зерен в пробе материала, a W - их общая масса.

Таким образом, для построения функции распределения по числу зерен следует по оси абсцисс на интервале х_п  х_п-1 построить прямоугольник высотой N_n / N Δх_п, а затем - прямоугольники для всех других классов и соединить кривой точки на серединах верхних сторон прямоугольников. Относительное число зерен в бесконечно малом интервале dх

и в классе х_п  х_п-1

.

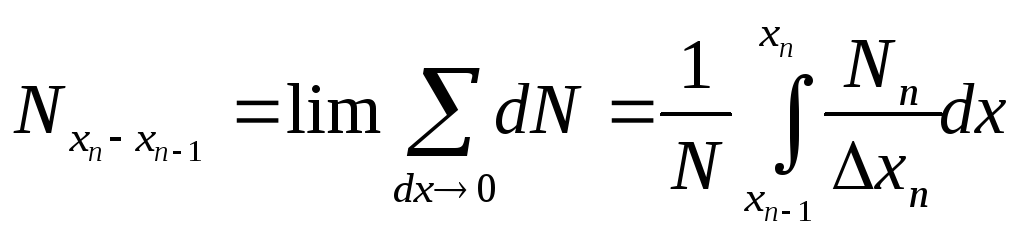Аналогично имеем следующее выражение для массовых выходов зерен класса х_n — х_п1;

.

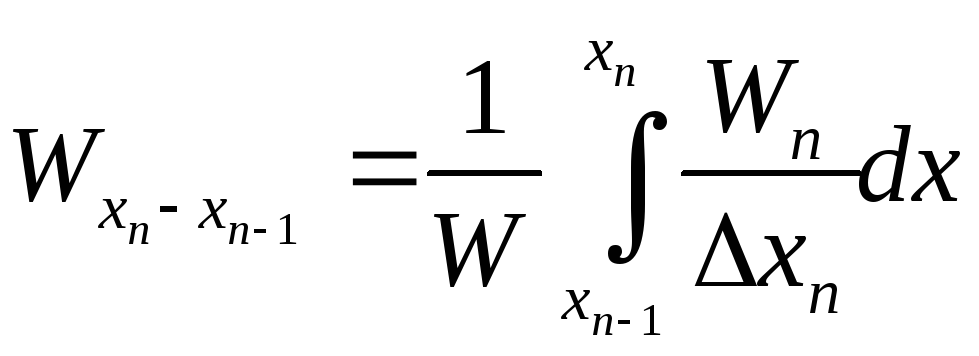Последнее выражение соответствует уравнению (4.19): в следующей записи

.

В этом уравнении пределы интегрирования определяют границы класса крупности, массовый выход которого определяется, а подынтегральная функция f(x) есть дифференциальное распределение по крупности.

Кривые распределения дают более наглядное представление о гранулометрическом составе сыпучих материалов в сравнении с суммарными характеристиками крупности. В классах с наибольшим выходом кривая показывает максимум, а при отсутствии в материале зерен какого-либо размера падает до нуля. Выход класса на кривой распределения пропорционален площадям, ограниченным кривой и двумя ординатами, проведенными на диаметрах, ограничивающих данный класс.

Дифференциальные функции распределения и суммарные характеристики крупности полностью характеризуют гранулометрический состав материала с точки зрения математической статистики. Возможен аналитический переход от одной кривой к другой, если известно уравнение какой-либо из них (см. формулу 4.19).