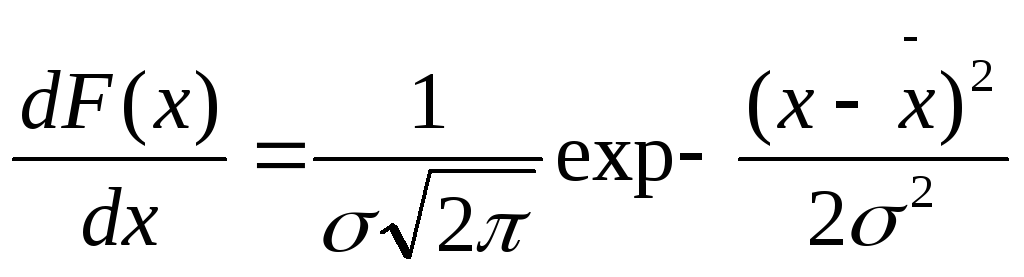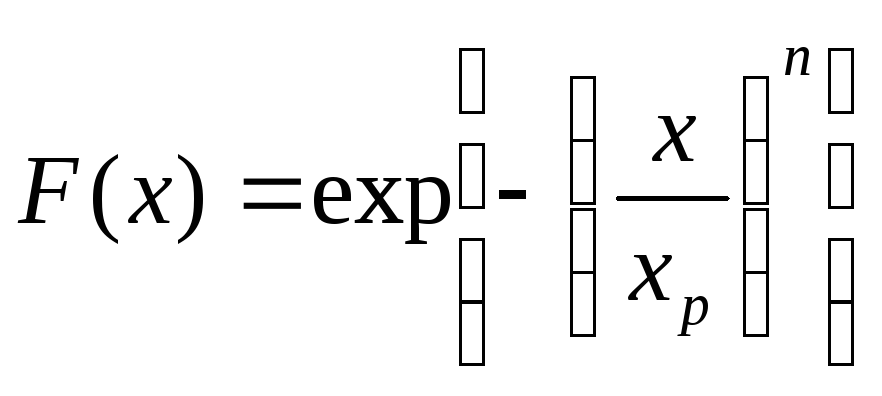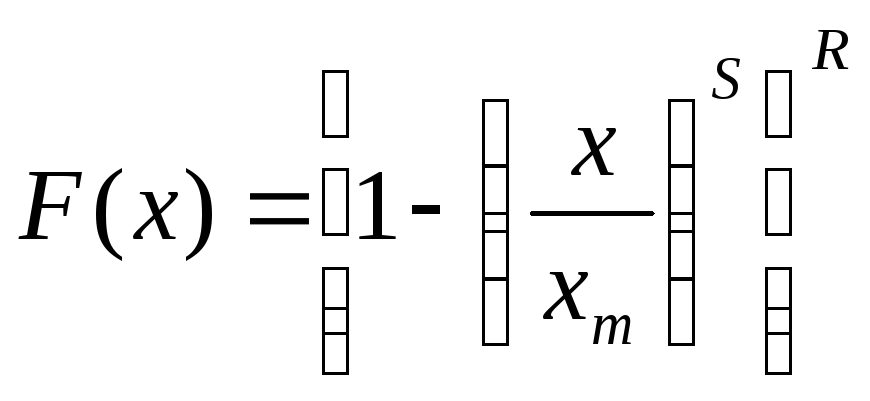4.2.6. Аналитическое представление характеристик крупности

Гранулометрические характеристики крупности могут быть представлены в аналитической, табличной форме или графически. Интегральная характеристика f(x) представляет интегральную функцию распределения частиц крупности x; она связана с частной (дифференциальной характеристикой) F(x) соотношением

. (4.19)

Наиболее общее выражение интегральной гранулометрической характеристики (функция распределения по крупности) имеет вид

, (4.20)

где - суммарный выход зерен крупности меньше размера отверстий х; х* - крупность, принятая для сравнения.

Поскольку х* есть оценка некоторой средней крупности частиц, то часто ее определяют как модуль крупности. Когда уравнение включает верхний предел крупности (например, уравнение Годэна-Андреева), х* фактически представляет максимальную крупность частиц в распределении. Если уравнение не включает верхнего предела (например, уравнение Розина-Раммлера), х* обычно ближе к истинному среднему.

Уравнение типа (4.20) также включает второй параметр, который может быть назван модулем распределения, поскольку он является мерой формы характеристики крупности. В некоторые уравнения включают третий параметр, связанный с асимметрией гранулометрической характеристики, но это осложняет проблему, что редко оправдывается. Некоторые наиболее общие случаи подобных (4.20) уравнений даны в табл. 4.14.

Таблица 4.14

Уравнения гранулометрических характеристик крупности частиц

Аналитическая функция	Математическое уравнение	Параметры уравнения	Примечание
1	2	3	4
Нормальное распределение		- среднее арифметическое; - стандартное отклонение	Действительные смеси частиц редко могут быть описаны этой функцией, поскольку большинство распределений асимметричны
Логарифмически-нормальное распределение		,	В некоторых случаях этому распределению подчиняются продукты дробления
1	2	3	4
Уравнение Розина-Раммлера		- крупность, при которой ; п - константа, характеризующая исследуемый материал	Хорошо согласуется с экспериментальными данными по смесям измельченных материалов
Уравнение Годэна-Андреева		xmax - модуль крупности, отрезок отсекаемый на оси крупности при F(x) = 1; k - константа, модуль наклона распределения логарифмической характеристики	Делает возможным использование стандартной логарифмической координатной бумаги
1	2	3	4
Уравнение Харриса		хт - максимальная крупность в пробе; S - параметр, связанный с наклоном логарифмического графика в тонком диапазоне крупностей; R - параметр, связанный с наклоном логарифмического графика в грубом диапазоне крупностей	Наиболее применим для описания полимодальных распределений

Если логарифмическая суммарная характеристика «по минусу» прямолинейна, то для того материала гранулометрический состав можно представить уравнением

,

где - суммарный выход класса мельче отверстий сита («по минусу»); k - коэффициент, равный тангенсу угла наклона прямой; х - размер отверстий сита; - отрезок, отсекаемый прямой на оси ординат.

Следовательно,

. (4.21)

Уравнение (4.21) суммарной характеристики, построенной «по минус х», известно под названием уравнения Годэна-Андреева.

Значение показателя k определяет направление и степень изгиба кривой характеристики. Если характеристику построить «по плюс х», то она будет: при k<1 выпуклой, при k = 1 прямой, при k<1 вогнутой. Следовательно, по значению показателя k можно судить о преобладании в материале крупных или мелких зерен.

Из уравнения (4.21) при х = х_тах; имеем .

Значение параметра А при данном показателе k зависит от диаметра максимального зерна материала x_max.

Уравнение характеристики позволяет решать ряд задач, например определять число зерен в любом классе, поверхность зерен, удельную поверхность и т. п.

Параметры уравнения находят следующим образом. На логарифмической характеристике выбирают две точки, соответствующие двум наиболее удаленным диаметрам, и определяют показатель k как тангенс угла наклона прямой:

.

Параметр А находят подстановкой значения k в уравнение (4.21) для одной из точек:

.

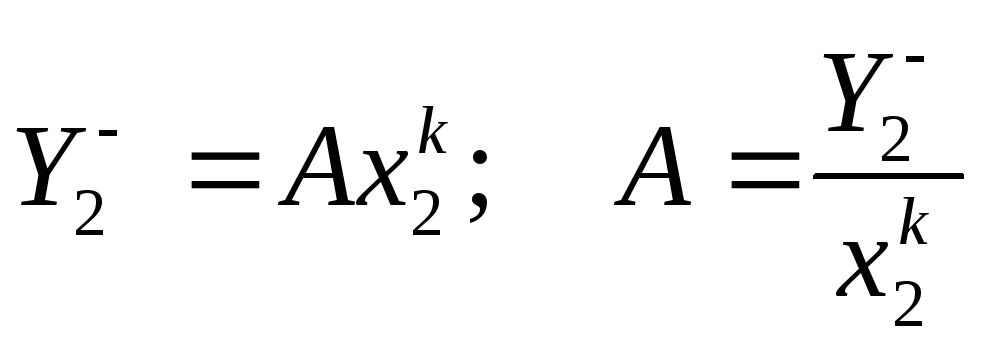Если диаметры зерен брать по отношению к диаметру максимального куска в материале, то уравнение Годэна-Андреева преобразуется в «приведенное» уравнение с одним постоянным параметром

или, если выражено в долях единицы, .

Показатель k находят описанным выше вычислением или, если принять за исходные для расчета x₂ и x₁ = x₂/2, то

. (4.22)

Для продуктов шаровых мельниц значение показателя k в уравнениях характеристик крупности находится в пределах 0,7-1.

Анализ большого числа гранулометрических анализов продуктов дробления и измельчения показала, что во многих случаях лучшее соответствие опытным данным по сравнению с уравнением Годэна-Андреева дает уравнение, предложенное Розиным и Раммлером:

, (4.23)

где R - суммарный выход класса, крупнее х, по «плюсу», %; х - размер отверстий сита; b и п - параметры, зависящие от свойств материала и размерности х.

Соответствие опытных данных уравнению (4.23) можно проверить графически путем нанесения опытных точек на функциональную координатную систему. При двойном последовательном логарифмировании уравнение (4.23) приобретает вид

.

В координатах уравнение Розина-Раммлера изображается прямой линией с угловым коэффициентом п. Пример построения такого графика (по данным табл. 4.12) показан на рис. 4.14, д.

На осях против соответствующих логарифмических величин приведены выхода классов и диаметры зерен материала.

Параметры b и п уравнения (4.23) находят по двум известным точкам, решая систему уравнений:

;

.

При совместном решении этих уравнений получим

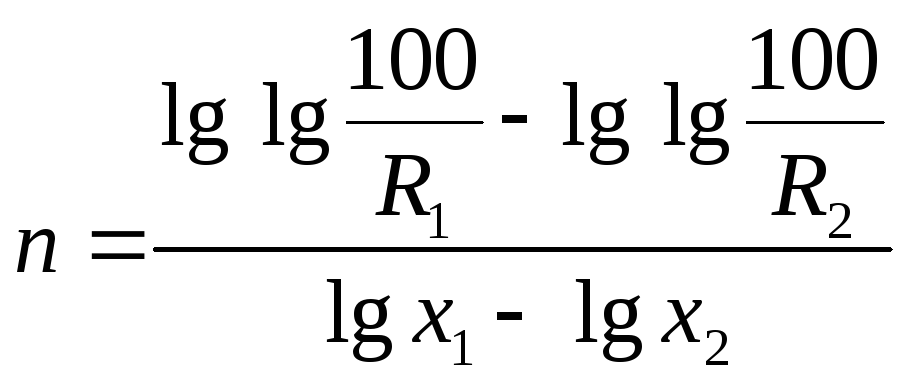. (4.24)

Зная n, определяем b:

;

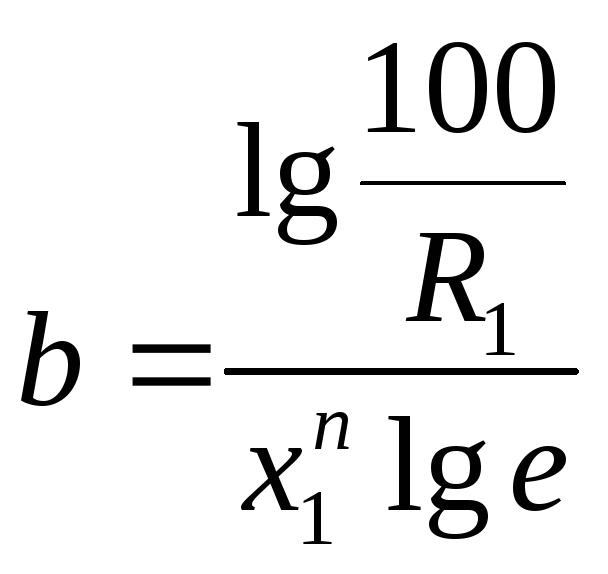. (4.25)

Уравнение Розина-Раммлера охватывает опытные точки в широком диапазоне крупностей, но оно не удовлетворяет одному конечному условию - нулевой выход классов достигается только при бесконечно большой крупности материала:

и R=0 при х = ∞.

При использовании уравнения Розина-Раммлера следует учитывать это обстоятельство и принимать конечную крупность материала, соответствующую какому-то определенному значению выхода класса. Сливы классификаторов шаровых мельниц, работающих в замкнутом цикле, большей частью удовлетворяют уравнению Розина-Раммлера при п = 1.