Пример. «Быть деревянным», «иметь четыре ножки», «иметь мягкое сиденье» - все это несущественные признаки стула, так как мы вполне можем помыслить себе стул, не являющийся деревянным, не имеющий четырех ножек, имеющий твердое сиденье. «Быть совершенным ночью», «быть страшным», «быть совершенным одним человеком» - все это несущественные признаки престспления, ибо мы вполне можем помыслить преступление и без этих признаков. «Переводить образ литературы на язык графики» - несущественный признак в основном содержании понятия «иллюстрация», поскольку мы можем помыслить иллюстрацию, переводящую образ литературы на язык живописи, а не графики.

Из приведенного определения можно извлечь и дальнейшую информацию о существенных признаках. Мы можем сказать, что признак является существенным для данного объекта, если этому объекту нельзя приписать признак, противоречащий данному.

Так, стулу нельзя приписать признак «иметь подлокотники», ибо получится кресло, нельзя ему приписать и признак «не иметь спинки», так как получится табуретка и т.п.

Чтобы определить, является ли признак существенным или несущественным, нужно задать следующий вопрос:

«Можно ли найти такой объект, входящий в объем данного понятия, который не имеет этого признака?»

Если вы ответите на него «да», то данный признак несущественный, если же вы ответите «нет», то этот признак существенный.

Пример. Рассмотрим понятие «университет» и признак «быть высшим учебным заведением». Наш вопрос будет выглядеть следующим образом: Можно ли найти такой университет, который не был бы высшим учебным заведением? Ответ на этот вопрос: «Нет». Следовательно, этот признак является существенным для понятия университет.

Рассмотрим понятие «человек» и признак «иметь образование». Наш вопрос будет выглядеть следующим образом: Можно ли найти такого человека, который не имел бы образования? Ответ на этот вопрос: «Да». Следмвательно, этот признак для понятия человек не является существенным¹.

В. Отличительные и неотличительные

Мы помним, что понятие не только сообщает нам существенную информацию об объектах, но и отличает объекты данного множества от всех иных объектов. Поэтому важно еще раз² рассмотреть, что такое отличительный признак для данного понятия.

Но вы догадываетесь, что он является существенным для понятия «студент». Первый раз мы его рассматривали в конце § 1 главы 3.

Отличительным для данного понятия назовем признак, если не существует такого объекта, который не входит в объем данного понятия, но обладает указанным признаком.

Проще, можно сказать, что признак отличителен для данного понятия, если он присущ только объектам, входящим в объем данного понятия.

Пр и м е р . Признак «быть общей частью родственных слов» является отличительным для класса предметов, являющихся корнями слова. «Предусмотренность уголовным законом» - отличительный признак понятия «преступление».

Признак называется н е отлич и те ль н ы м для дан н ого пон ят ия, если существует такой объект, который не входит в объем данного понятия, но обладает указанным признаком.

Проще, можно сказать, что признак неотличителен для данного понятия, если он присущ не только объектам, входящим в объем данного понятия.

Пр и м е р . Признак «иметь спинку» присущ не только стульям, а «быть общественно опасным» - не только преступлениям.

Чтобы установить, является признак отличительным или нет, следует задать следующий вопрос:

«Существует ли такой предмет, который не входит в объем рассматриваемого понятия, но тем не менее имеет данный признак»?

Если ответ на этот вопрос - «да», то признак неотличирельный, если - «нет», то признак отличительный.

Пример. Рассмотрим понятие «четное число» и признак «делиться на два без остатка». Наш вопрос будет выглядеть следующим образом: Можно ли найти число, не являющееся четным и делящееся на два без остатка? Ответ на этот вопрос: «Нет»». Следовательно, этот признак является отличительным для понятия «четное число».

Рассмотрим понятие «книга» и признак «быть источником знаний». Наш вопрос будет выглядеть следующим образом: Можно ли найти такой источник знаний, который не является книгой? Ответ на этот вопрос: «Да, например, «Интернет». Следовательно, этот признак не является отличительным для понятия «книга».

Однако при более длительной работе с понятиями замечаешь, что в содержании многих понятий нет простых отличительных признаков, а они тем не менее прекрасно отличают предметы данного класса от всех остальных предметов. Почему так случается? Дело в том, что по отдельности неотличительные эти признаки, взятые вместе, могут выполнять задачу отличения. Поэтому нам придется ввести понятие сложного отличительного признака. Иногда мы будем называть такой признак «достаточным» для данного понятия.

Сложный признак P, состоящий из простых неотличительных признаков P P P_n называется отличительным (или достаточным) для понятия A, если не

существует такого предмета, который не входит в объем понятия A, и вместе с тем обладает всеми признаками P , P P_n одновременно.

Несложно заметить, что при помощи отличительных признаков решается задача выделения предметов интересующего нас множества из всех остальных предметов.

Объем понятия

Вторая логическая характеристика каждого понятия - объем - это те мыслимые в понятии объекты, ради выделения которых из всех других объектов и образуется содержание понятия.

Поскольку объем понятия представляет собой множество, то нам придется овладеть некоторыми самыми элементарными сведениями из теории множеств.

Первоначальному понятию теории множеств - множеству - нельзя дать определения. Его можно только пояснить. Под множеством в дальнейшем мы будем иметь в виду совокупность объектов, которые мы по тем или иным основаниям способны мыслить вместе.

Люди, студенты, звезды, понятия - все эти предметы, мыслимые вместе, образуют множества. Коллектив, созвездие, полк - это тоже множества людей или звезд. Множество может быть задано двояко: 1) при помощи некоторого признака или 2) при помощи списка. В предложении - «Студенты Боброва, Курпаков и Юдина могут покинуть аудиторию» - множество задается списком. В предложении - «Студенты, сдавшие контрольную работу, могут покинуть аудиторию» - множество задается при помощи общего признака.

Таким образом, любые объекты, которые мы мыслим вместе и которые мы можем объединить либо списком, либо при помощи общего признака, будут составлять множество.

Об отдельном объекте, из числа тех, что образуют данное множество, мы будем говорить, что этот объект входит в данное множество или объекта принадлежит данному множеству.

Объект a будем называть элементом множества A, если он входит в множество A.

Этот факт мы будем записывать следующим образом:

a g А.

Множество А будем называть подмножеством множества В, если каждый элемент А в то же время является элементом В.

Это мы будем записывать так:

А^В

Множество А будем называть собственным подмножеством множества С, если А — подмножество С и существует хотя бы один элемент С, который не является элементом множества A.

Это мы будем записывать так:

Для обозначения множеств мы будем использовать те же прописные буквы начала латинского алфавита, набранные курсивом, что и для обозначения понятий. Основанием для этого служит тот факт, что содержание понятия есть признак, по которому можно образовать множество. К тому же из контекста употребления этих обозначений всегда будет ясно, о чем идет речь: о понятии или о множестве.

Для понимания теории понятия нам понадобится некоторое представление о простых операциях с множествами таких, как пересечение и объединение множеств, а также дополнение к множеству.

Пересечением множеств A и B будем называть множество тех элементов, которые одновременно входят в A и B.

Более формально: АгчВ = множество а таких, что a g A n a g В.

Пример. Пересечением множеств студентов и отличников будет множество студентов-отличников, а пересечением множеств греческих богов и кузнецов будет множество, состоящее из единственного элемента - бога-кузнеца Гефеста. Пересечением множества книг и учебных пособий будет множество учебников.

Объединением множеств A и B будем называть множество элементов, которые входят в A или в B.

Более формально: А^иВ= множество а таких, что а e А или а e В.

Пример. Объединением множеств газет и журналов будет множество периодических изданий, а объединением множеств четных и нечетных чисел - множество натуральных чисел.

Операции с множествами удобно иллюстрировать при помощи графических схем, в которых множества представляются в виде кругов, и предпойагается, что в этих кругах заключены все элементы данного множества. Такие круги называются кругами Эйлера, по имени немецкого математика Леонарда Эйлера, который в 1762 году приспособил эту геометрическую фигуру для логических целей.

Пример. Множество стульев мы изобразим следующим образом:

Внутри круга, изображенного на рис. 1, находятся все возможные стулья.

Отдельный элемент будем обозначать точкой в круге, единичное множество —

кругом.

Пример. Множество русских царей изобразим при помощи круга, а отдельный элемент, например, Александра П - точкой в круге:

Русский царь

Рис. 2

Пересечение множеств студентов и отличников будет выглядеть таким образом:

Рис. 3

Заштрихованная часть - это множество тех элементов, которые одновременно принадлежат множествам студентов и отличников. Таким образом, в заштрихованной части, называемой пересечением множеств, находятся все студенты-отличники.

Объединение множеств студентов и отличников будет выглядеть следующим образом:

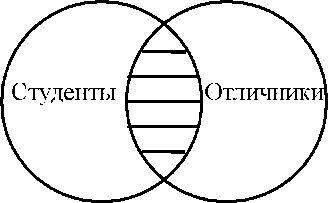
Заштрихованная область представляет собой объединение этих множеств, т.е. множество студентов или отличников. В него входят все студенты, а также все отличники. Каждый элемент является студентом или отличником, а некоторые элементы - одновременно студентами и отличниками (как видно на рис. 4).

Чтобы ввести еще одну важную операцию с множествами, нам понадобится одно новое понятие. Представим себе множество всех объектов, т.е. такое множество, для которого любое другое множество объектов, кроме него самого, является его собственным подмножеством.

Множество всех объектов U назовем универсальным множеством.

Поскольку любое множество A является подмножеством этого множества, то мы для любого множества можем рассмотреть операцию, дополняющую это множество до универсального. Эта операция так и называется - дополнение. Графически ее можно изобразить следующим образом:

Рис. 5

Заштрихованная часть представляет собой дополнение A. Символически дополнение будем изображать так - A .

Можно рассматривать дополнения не тмлько к отдельному множеству, но и к пересечениям и объединениям множеств.

Существуют простые взаимоотношения между пересечением, объединением и дополнением множеств:

АиВ=АпВ АпВ=АиВ

Кроме универсального, существует еще одно специальное и единственное множество, которое не содержит ни одного элемента.

Множество, не содержащее ни одного элемента, называется пустым множеством.

и будем обозначать его 0

Существуют простые взаимоотношения произвольных множеств с универсальным и пустым:

AuA = U Агл~А = Сд Ū = 0 0 = U

Операции пересечения и объединения могут быть, как в арифметике операции умножения и сложения обобщены на случай более чем двух множеств. Так, мы будем писать

Аг^ВглС. имея при этом в виду ((A n В) n С) . То же самое и для объединения.

Познакомившись с первоначальными понятиями теории множеств, перейдем к объему понятий.

Пусть множество A составляет объем понятия A.

Тогда собственное подмножество B множества A будем называть частью объема понятияA.

Проще говоря, часть объема понятия - это более одного элемента объема понятия, но не все.

Элементом объема понятия будем называть элемент множества, составляющего объем понятия.

Чтобы эффективно оперировать в дальнейшем с объемами понятий, следует иметь в виду следующее правило объема:

Каждый элемент объема понятия имеет все признаки, перечисленные в содержании понятия.

Итак, если вы хотите установить, является ли некоторый предмет элементмм объема данного понятия, проверьте, имеет ли он все признаки, которые вы мыслите в (основном) содержании данного понятия. Это правило особенно существенно для понятий типа: коллектив, созвездие, преступная группа, множество, лес и т.п. Обратите внимание, что пользуясь этим правилом, можно объяснить, почему отдельные люди, звезды, преступники, предметы, деревья не являются элементами объема этих понятий, и заодно понять, что же является элементами их объема.