§45. Касательная плоскость и нормаль к поверхности

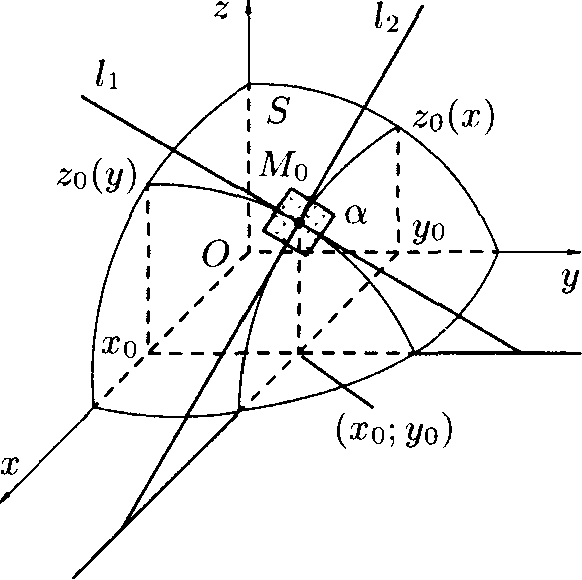
Рассмотрим одно из геометрических приложении частных производ­ных функции двух переменных. Пусть функция z — f{x:y) дифференци­руема в точке (хо;уо) некоторой области D Е К². Рассечем поверхпоп ь S. изображающую функцию z. плоскостями .г = .го и у = у о (см. рис. 209). Плоскость х = хо пересекает поверхность 5 no irt•-которой линии Zq(ij). уравнение которой пол\ чается подстановкой в выражение исходной функции : --=f{^x', у) вместо ,т чиста .г₍₎. Точка U₀(.r₀: г/.,: f{x,y. i/u)) принадлежит кривой ~₍₎(//). В силу дифферспциру-емости функции z в точке Л/о (функция z_{)(y) шкжс является дифференцируемой в ючке у — ,</(,. Слодо-вательно, в этой точке в плоскости ./• = .г о к к|)ивой ^zo(y) может быть проведена касательная I\.

Рис. 209.

Проводя аналогичные¹ рассуждения для сечения у = уо, построим касат(\чы1ук) !■> к кривой со(.г) в точке х = Х(). Прямые /| и !■> определяю! м.'юскость а, которая называется касательной плоскостью к поверхности S в точке М_п.

Составим ее уравнение. Так как плнекоси. а проходит через точку Мо{хо',Уо'-, -о)- го ее уравнение¹ может бып> записано

в виде

A(x-x_o) + B(y-y₍₎)+C(z-z_t))=0.

которое можно переписать так:

1)

z - z₀ = At (.т - .г„) + 17, (у - у₀)

(разделив уравнение на —С и обозначив Найдем .4i и £?,.

А _ . В

= /?,

С

С

Уравнения касательных 1\ и \-> имеюч вид z~ z₀ = f'_!t(.(.-₀;//()) • (.</ -i/o). z - z₀ = fs{xo;?/о) • (.г -.го).

= А,

.'/

Ни

соответс: твенно.

Касательная 1\ лежит в плоскости о, следовательно. коорлшип ы всех точек 1\ удовлетворяют уравнению (45.1). Этот факт можно записан, в виде системы ,

г - 2₀ - /i(-''o-?/<))(.'/ ~ Но),

х = х₀,

z - z₀ - А, (./: - .го) + В\ (у - //о).

Разрешая эту систему относительно П[, получим, что П\ = /у(.''о: </о)-Проводя аналогичные рассуждения для касательной Ь- -нч ко устано­вить, что А₁ = f'_x(x₀;y₀).

Подставив значения А] и В\ в уравнение (45.1). получаем искомое уравнение касательной плоскости:

^z ~ ^zo = f'_r(^xo;yo) ■ (•*-' - :<-'о) + Д(•''(); г/и) • (у - .*/(>)■

45.2)

273

о

Прямая, проходящая через точку Л/о и перпендикулярная касательной плоское i и. построенной и '-пой ючкс поверхности, называется ее норма­лью.

Используя условие перпендикулярное!и прямой и плоскости (см. с. 87). легко получить канонические уравнения нормали:

.;■	- ■'"■<)	У -	- Уо	- 1 '
/.!■(•	"о: .</( 1)

(45.3)

_s

К(„1н поверхность .S задана уравнением F(.r:i/:z) ~ 0, то уравнения (4-7.2) п (4-7.3). с учетом юго. что частные пропзволныо могут быть найде­ны как uponsполные неявной функции:

,,-, , К (■'■»: .'/"1 г/, ч ^'(./:₍₎;.у„)

^Л-'о:.'А|) ^(•'■о:.(/о)

(см. формулы (44.12)), приму! соответственно вид

F'Uv .'А)) ■ (.'■ - -'и) Л F',(r„: //„) ■ (у - ,/„) + F'. (./•„:,/(,) - (\: - с₍₎) = О " •'■ - -'-о .'/ - (Ai ~ ^ л)

F',{.r г ■!/:,) F'_t (,г„://(,) F'(.n,:y₍,)' Зп.исшпш'. Формулы касательной плоскости и нормами к поверхности получены лля обыкновенных, i. о. не особых, точек поверхности. Точка Л/₍₎ поверхпос I н называется особой, если в -пой ючкс все частные производ­ные рампы пулю пли хзия Пы одна из них не гущеетиуе!. Такие гонки мы не расема триваем.

Пример J,~).\. Написать уравнения касательной плоскости и нормали к параболоиду вращения -. -- \:~ \- ц~ и точке Л /о (1; - 1:2).

.с- П-2-(,/ + 1) или 2.Г -2ц- :-2 = 0

1 _ :. - 2 _л

QlV'iiemie: Здесь :[ = J',(.r: „) = 2.г. /'„{.г; //) = 2у. f'_i.(h-l) = 2. /,',(!: -1) -- -2, Пользуясь формулами (1-7.2) и (4-7.3) получаем уравнение каса ю.ь.иой плоское! и: ; - 2 -• 2

г -- 1 (/ »- ! и уравнение нормали: —.-,-- - — .,-