§44. Производные и дифференциалы функции

НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 44.1. Частные производные первого порядка и их геометрическое

истолкование

Пусть задана функция г = f(x; у). Так как х и у — независимые пере­менные, то одна из них может изменяться, а другая сохранять свое значе­ние. Дадим независимой переменной х приращение Ах, сохраняя значение

263

у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается A_xz. Итак,

A_xz = f(x + Ах; у) - f(x; у). Аналогично получаем частное приращение z по у:

A_yz = f(x; у + Ay) - f(x; у). Полное приращение Az функции z определяется равенством

Az = f(x + Ах;у + Ay) - f(x;у). Если существует предел

lim %£ = lim f(* + **-'V)-ftov)_t Дж-s-o Да; Дх-s-o Да;

то он называется частной производной функции z = f(x; у) в точке М(х; у) по переменной х и обозначается одним из символов:

*' — Г ^д-1

*' dx^Jx' дх'

Частные производные по а; в точке Мо(хо',уо) обычно обозначают симво­лами f'_x(x₀;y₀), f_x ■

М₀

Аналогично определяется и обозначается частная производная от z = f(x; у) по переменной у:

г' = Нш bl _{= lim} f(x;y ₊ Ay)-f(x;y)_ ^у Ду->0 Ау Ду->0 Лу

Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных незави­симых переменных. Поэтому частные производные функции f(x; у) нахо­дят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной вели­чиной).

Пример 44Л. Найти частные производные функции z — 2у + е^х ~^v 4-1.

О Решение:

4 = (2у + е*²~У + 1)'_х = (2у)'_х + {е*²-У)'_х + (1)'_х =

= о + е*²-» ■ (х² -у)'_х+0 = е^х2~^у ■ (2х - 0) = 2х ■ е^х2~^у;

z'_y = 2 + е^х2~У •(-!). •

264

Геометрический смысл частных производных функции двух переменных

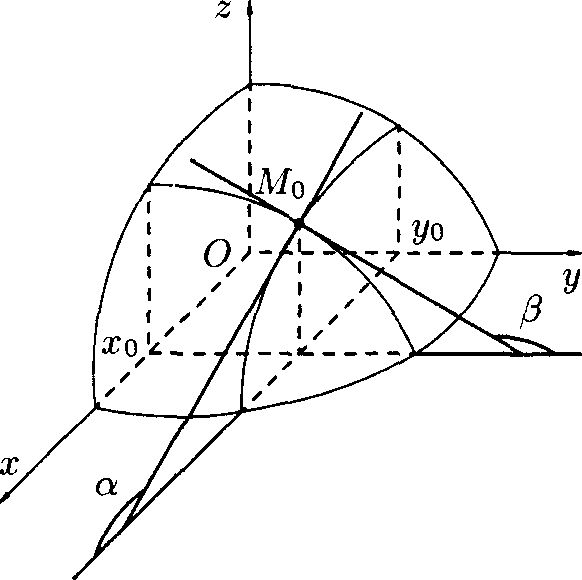
Графиком функции z = f(x;y) явля­ется некоторая поверхность (см. п. 12.1). График функции г = f(x;yo) есть линия пересечения этой поверхности с плоско­стью у = г/о- Исходя из геометрическо­го смысла производной для функции од­ной переменной (см. п. 20.2), заключа­ем, что /i(x₀;j/₀) = tga, где а — угол между осью Ох и касательной, прове­денной к кривой z — f(x;yo) в точке M₀(x₀;yo;f(xo;yo)) (см. рис. 208).

Аналогично, f_y(x₀;yo) = tg/3.

Рис. 208.

44.2. Частные производные высших порядков

Частные производные \. ' и ^J \ ' называют частными про­изводными первого порядка. Их можно рассматривать как функции от (х;у) S D. Эти функции могут иметь частные производные, которые на­зываются частными производными второго порядка. Они определяются и обозначаются следующим образом:

дхду

д_ (дг_ дх \дх

д_ (дг_ дх \ду

д_ (дг_ ду \дх

^1 дх²

d²z

дудх ^=z*v ⁼ f"v(^x>vy>

д²-

^ух Jyx\^X' У)

д (dz\ d²z

ду \ду) ду²

*vv = /£(*;«)■

Аналогично определяются частные производные 3-го, 4-го и т. д. порядков.

д

_ д d²z

d^Az

= ^{д г} дх ду дх

(4) 'хух²

О

Так, z"

= z

(или (г'"

ду \dxf)' дх Кдхдудх

1 хху И Т. Д.

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производ-

dh

"хух-

ной. Таковыми являются, например, z"„ „ „ л.

" дхду

Пример 44-%- Найти частные производные второго порядка функции

:Ж⁴ -2х²у³ +у⁵ + 1.

265

О Решение: Так как z'_x = 4х³ — 4ху³ и z'_y = —6х'²у² + 5у^&, то

г% = (4х³ - 4ху% = -12ху², z'_y^l_x = (-6x²y² + 5y⁴)'_x = -l2xy².

Оказалось, что z_xy — z'_y'_x. •

Этот результат не случаен. Имеет место теорема, которую припадем без доказательства.

Теорема 44.1 (Шварц). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком диффе­ренцирования, равны между собой.

В частности, для z = f{x;y) имеем: ^^ = ЩЪх'