41.4. Вычисление объема тела

Вычисление объема тела по известным площадям параллельных сечений

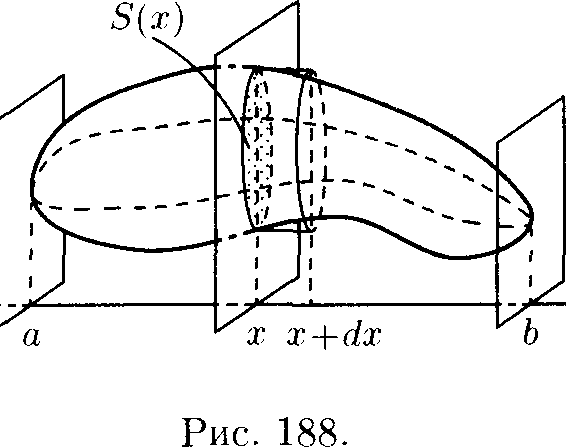
Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, порпондикулярными некоторой оси, на­пример оси Ox: S = S(x), а ^ х ^ Ь.

Применим схему II (метод дифференциала).

О

1. Через произвольную точку х £ [а;Ь] проведем плоскость П, перпендикулярную оси Ох (см. рис. 188). Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяю­щейся при изменении х. Через v(x) обозна-_ чим объем части тела, лежащее левее плос-^х кости П. Будем считать, что на отрезке [а; х] величина v есть функция от х, т. е. v = v(x) (v(a) = 0, v(b) = V).

245

2. 

   Находим дифференциал dY функции v = v(x). Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках х и х + Ах, который при­ближенно может быть принят за цилиндр с основанием S(x) и высотой dx. Поэтому дифференциал объема dV = S(x) dx.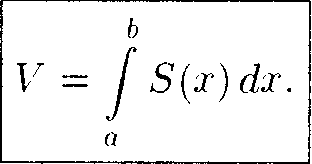

3. Находим искомую величину \' путем интегрирования dA в пределах от а до Ь:

(41.6)

о

Полученная формула называется формулой объема тела по площади параллельных сечений.

Пример 41-6. Найти объем эллипсоида

1С Ь²

1.

О Решение: Рассекая эллипсоид плоскостью, параллельной плоскости Oyz и на расстоянии .т от нее ( — я $J х ^ а), получим эллипс (см. рис. 189):

Z |	У/
да
	t-^x а х
ZlLL-	>>х
Рис. 189.

(bJl

г)² (<

П(

Площадь этого эллипса рашга Я(х) ~- Tihc[ 1 этому, по формуле (41.6). имеем

V

ттЬс I

(Г ' о

Объем тела вращения

П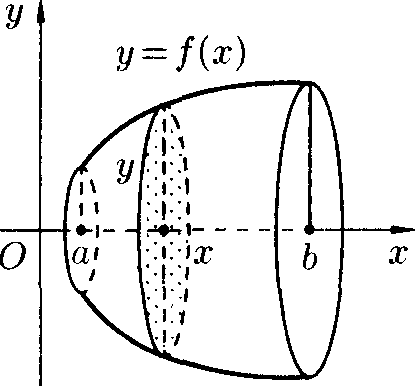 усть вокруг оси Ох вращается криволинейная гранения, ограничен­ная непрерывной линией у = /(.г) >, О, отрезком а ^ х ^ b и прямыми х — а и х — b (см. рис. 190). Полученная от вращения фигура называет­ся телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох. проведенной через произвольную точку х оси Ох, (х € [я;Ь]), есть круг с радиусом у — f{x). Следовательно. S(x) = тп/².

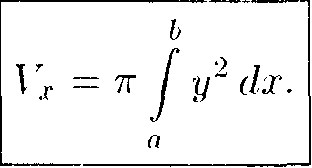
Применяя формулу (-11.6) объема тела по площади па­раллельных сечений, получаем

■41.7)

Рис. 190.

Если криволинейная трапеция ограничена графиком не­прерывной функции х = ~р{у) JJ 0 и прямыми .7- = 0, у = с.

246

d (с < d). то объем тела, образованного вращением этой трапеции

У

вокруг оси Оу, по аналогии с формулой (41.7). равен

d

V

(41.8)

- 7!" / X² dy.

Пример 41.7. Найти объем тела, образован­ного вращением фигуры, ограниченной линия­ми (/ — V- ^х ~ 0. у = 2\[2 вокруг оси Оу (см. рис. 191)"

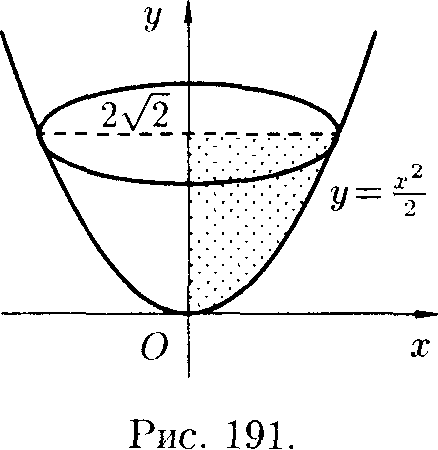
Q Решение: По формуле (41.8) находим:

2v/2

\'„

tv / 2ydy = vT/y~|~ " = 87г.

Вычисление площади поверхности вращения

Пусть кривая АВ является графиком функции у = f(x) ^ 0, где •г а [а;Ь]. а функция у = /(.г) и ее производная // = f'(-i') непрерывны па чтом отрезке.

Найдем площадь 5 поверхности, образованной вращением кривой АВ вокруг оси (1.г.

Применим схему II (метод дифференциала).

1. Ч 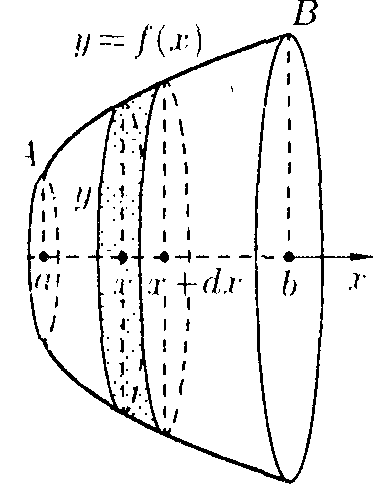ерез произвольную точку .;: £ [а;Ь] проведем плос­кость П, перпендикулярную оси Ох. Плоскость П пере­секает поверхность вращения по окружности с радиусом И — /(^;(;) (^гм- Р¹"'- 192). Ветчина S поверхности части фи­гуры вращения, лежащей левее плоскости, является функ­цией 0 1 .с. т. е. .s = s(.r) (sia) - 0 и s(b) = S).

2. Дадим аргументу х приращение Д.г = dx. Через точ­ку х + d.r (z [u'.b] также проведем плоскость, перпендику­лярную оси Ох. Функция .s = s(x) получит приращение А*, изображенного на рисунке в виде «пояска».

Рис. 192

Найдем дифференциал площади ds, заменяя образо­ванную .между сечениями фигуру усеченным конусом, об­разующая которого равна dl, а радиусы оснований рав­ны у и у + dy. Площадь его боковой поверхности равна ds — тт(у + у + dy) ■ dl — '1~у dl + 7г dy dl. Отбрасывая произведение dy dl как бесконечно малую высшего порядка, чем ds, получаем ds = 2irydl, или, так как dl = \/l + (у',.)² dx. то ds = 2~y\J\ + (y'_r)- dx.

3. Интегрируя полученное равенство в пределах от х — а до х ~ Ь, получаем

S_J. = 2nJ_u-_y/l + {y^,_x)²dx.

(41.9)

217

Если кривая АВ задана параметрическими уравнениями х = x(t), у = y(t). ti ^ t ^ t?, то формула (41.9) для площади поверхности вращения прини­мает вид

S_x = 2п J y(t) • s/(x'(t))² + (y>(t))²dt.

Пример 41-8. Найти площадь поверхности шара радиуса R.

О Решение: Можно считать, что поверхность шара образована вращением полуокружности у — \/R² — х², —R <С х <С R, вокруг оси Ох. По форму­ле (41.9) находим

S = 2тт

^{j ^-x*.f7(}

-я ^v

VR² - т²

dx

lir f s/r

² - .r- + x² dx = 2nR ■ x " = 4тгR-. •

I — л

Пример 41-9- Дана циклоида

J и- = a(t - suit), 1 у — a{\ — eosf),

0 $ t й 2тг.

Найти площадь поверхности, образованной вращением ее вокруг оси Ох.

О Решение: При вращении ио.товины дуги циклоиды вокруг оси Ох пло­щадь поверхности вращения равна

~S_X = 2тг I а{\- cos 0 • i/(«(l -cos*))² + (« sin f )² Л = о

= 2тг / а² • 2 sin² - • v/l - 2 cos * + cos'² / + sin² t dt = 6

= -lira / sin -

2 • 2 sin² - dt = 8тта'² / sin² - • sin - dt о

2 1б7га

" cos³ ~

")

и /

о 3

., ( 2\ 32/та" 3 '

-8тга² ' ² /' (l - cos² ~) rifcos 0 = -16тго² (cos ^

0

-KWVo- 1 -()+ij = _Ю7га²(-^)

1с _32

'!• е. i5j = ^~тта². Следовательно. S_x

64_2

248