§37. Формула ньютона-лейбница

Пусть функция у — /(.г) интегрируема на отрезке [reft].

Теорема 37.1. Если функция у = /(.с) непрерывна на отрезке [a: ft] и F(x) какая-либо ее первообразная на [a; ft] (F'(-r) = fix)), то имеет место формула

ь

f f(x)dx = F(b)~F(o). (37.1)

Q| Разобьем отрезок [я; ft] точками а — хц. х.\ ft = х„ (.Со < Х\ < ■■■

■ ■ ■ < х_п) на п частичных отрезков [.Г(>; ху]. [х\; х-±\ [х_п -1: ./•„]. как это

показано на рис. 169.

П С> С; г;„ X

1 1—•—I—•—I—•—I—•—I—•—I—•—I—•—I—•—I —

О а = ха х\ г-2 j",-_i х, Ь = х„

Рис. 169.

224

Рассмотрим тождество

F(b) - F(a) = F{x„) - F(x₀) = (F(s„) - F(x_n-₁)) +

+ {F(x_n-i) - F(x„--₂)) + ■■■+ (F(x₂) - F(n)) + (F(n) - F(x₀)). Преобрачз'ем каждую разность в скобках по формуле Лагранжа

f(b)-f(a) = f'(c)-(b-a). Получим

F(b) - F(a) = F'(c_n) ■ (_Хп - x_u-i) + F'(c„-i) ■ (i»-i - x_n.₂) + ...

П П

■■■ + F'(o₂) ■ (x₂ -_Xl) + F'(c!)(a:i - x₀) = £ F'(a)Axi = £ /(r,)A.r,

т. e.

j=i

F(b)-F(a) = Y_if(c_i)Ax_i,

(37.2)

где г, есть некоторая точка интервала (#*_!; х,). Так как функция </ = /(.г) непрерывна на [а; Ь]. то она интегрируема на [а:Ь]. Поэтому сущее пн ег предел интегральной суммы, равный определенном}' интегралу oi /(./■) па [а; Ъ].

Переходя в равенстве (37.2) к пределу при А = max Дх, —► 0, нол> чаем

F(b)-F(a)=limT_ff(c_i)Ax_i,

А->0 '—'

т. е.

		7 = 1
F(b)-	- F(«) =	Ь = ffHdx. a

Равенство (37.1) называется формулой Ньютона-Лейбница.

Если ввести обозначение F{h) — F(a) = F(x)\ , то формулу Ньютона Лейбница (37.1) можно переписать так:

ь

ff(x)dx = F(x)\

Формула Ньютона- Лейбница дает удобный способ вычисления определен­ного интеграла. Чтобы вычислить определенный интеграл от непрерывной функции f(x) на отрезке [а; Ь], надо найти ее первообразную функцию F(x) и взять разность F(b) — F(a) значений этой первообразной на концах от­резка [а;Ь].

з

Например, / х~ dx

/_|" -0-0 = 9 ₃ |₀ J и у,

_{■/rf^ = *Mrt«fl>i(}-(-})) = !■}

Пример 37.1. Вычислить интеграл / w ^c?^s dx.

225

О Решение:

7Т Г. Z 7Т 7Т

/ ./ —-dx = / Vcos'² xdx = / |cos;r|(ia: =

о V о о

= cosxdx + (—cosx)dx = smx\^+(—s'mx)\^7T_!L=l + l = 2.

dx 1 х'

Пример 37.2. Вычистить интеграл / —у-

d

О Решение: / —-— = In I Inх\Г = In2 - In 1 = 1п2. ^ J х\пх ' ^Ие

§38. Основные свойства определенного интеграла

Рассмотрим основные свойства определенного интеграла, считая подынтегральную функцию интегрируемой на отрезке [а: Ь]. При выводе евойс тв будем использовать определение интеграла и формулу Ньютона Лейбница.

1. Если с — постоянное число и функция f{x) интегрируема на [а:Ь],

^то ь ъ

j с ■ }{х) dx = с ■ j f{x) dx, (38.1)

т. е. постоянный множитель с можно выносить ча знак определенного ин­теграла.

Q| Составим интегральную сумму для функции с • f(x). Имеем:

11 п

^с./(с,)А.г₍=с-^/(_С;)Ах₍,

ь Тогда lim J2 c,-f(x)Axj — с- lim J2 f{^ci) ⁼ <"' / f(^x) dx. Отсюда вытекает.

a

что функция r-f(x) интегрируема на [a; b] и справедлива формула (38.1).

■

2. Если функции fi(x) и /2(2:) интегрируемы на [а;Ь], тогда интегри­руема на [п:Ь] их сумма и

ь ь ь

j (/1 (а;) + h (•>•)) dx = J f_x (x) dx + J /₂(x) dx, (38.2)

a a a

т. е. интеграл от суммы равен сумме интегралов.

226

□ f(fiH + f.₂{x))dx= lim V(/₁(c,) + /₂(c,)]A.r, =

/=1

- lim V/i(r,)A.r;+ lim V h(ci)A_Xi = ff₁(x)dx+ f f₂(x)dx. ■

' = 1 '=1 a a

Свойство 2 распространяется на сумму .тюбого конечного числа сла-

гаемых.

ь

I f(x)dx = - I f(x)dx.

Это свойство можно принять по определению. Это свойство также под­тверждается формулой Ньютона -Лейбница.

Ь а

I f(x) dx = F(b) - F(a) = -(F(a) - F(b)) = -J f(x) dx.

n b

4. Если функция f(x) интегрируема на[а:Ъ] и а < с < Ъ, то

Ь с Ь

I /(.г) dx = I f{x) dx + J f(x) dx, (38.3)

а а с

т. е. интеграл по всему отрезку равен сумме интегралов по частям этого о гречка. Это свойство называют аддитивностью определенного инте­грала (или свойством аддитивности).

[_} При разбиении отрезка [а;Ь] на части включим точку с в число точек деления (это можно сделать ввиду независимости предела интегральной суммы от способа разбиения отрезка [га; 6] на части). Если с = х,_п, то интегральную сумму можно разбить на две суммы:

и т п

£/(с,)Лт, = £/(г;)Д*/ + £ Д^С.-)Д**-

/— 1 /'= 1 i = m

Каждая из написанных сумм являегся интегральной соответственно для отрезков [а: Ь], [«; г] и [с;Ц. Переходя к пределу в последнем равенстве при п —► ос (А —> 0), получим равенство (38.3). И

Свойство 4 справедливо при любом расположении точек я, 6. с (счита­ем. ччо функция /(.г) интегрируема на большем из получающихся отрез­ков).

Так. например, если а < b < с. то

с Ь с

f f(x)dx= Jf(x)dx + J f(x)dx.

Очсюда

ь

j /(.,■) dx = j f(x) dx - I fix) dx = J f[x) dx + J fix) dx

b

(использованы свойства 4 и 3).

227

о. «Теорема о среднем». Если функция f(x) непрерывна на отрезке [a; b], то существует точка с е [а; b] такая, что

I f(x)dx = f(c)-{b-a).

Q| По формуле Ньютона-Лейбница имеем ь I f(x)dx = F(x)\^b_a=F(b)-F(a),

а

г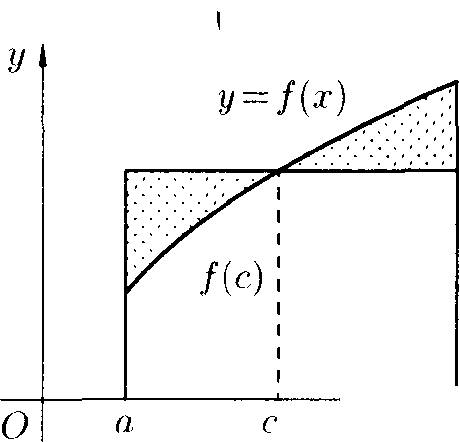 де F'(x) = f(x). Применяя к разности F(b) — F(a) теорему Лагранжа 'теорему о конечном приращении функции), получим

F(b) - F(a) = F'(c) ■ (b - a) = f(c) ■ (b - а). Ш

Свойство 5 («теорема о среднем») при /(.г) ^ 0 име­ет простой геометрический смысл: значение определен­ного интеграла равно, при некотором с € (а;Ь), площа­ди прямоугольника с высотой /(г) и основанием Ь — а (см. рис. 170). Число

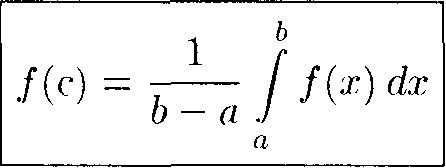
b ^х

Рис. 170.

qX называется средним значением функции f(x) на отрезке [а; Ц.

—■ 6. Если функция /(.т) сохраняет знак на отрезке [а; Ь], где а < Ь, то un-

it

теграл I f(x)dx имеет тот ж-,е знак, что и функция. Так. если f(x) ^ 0

а

b

на отрезке [а\Ъ], то / f(x)dx ^ 0.

а

Q| По «теореме о среднем» (свойство 5)

ь jf(x)dx = f(c)-(b-a),

а

где с € [а; Ь]. А так как f(x) ^ 0 для всех х € [а; Ь], то и

/(г) ^ 0, Ь-а>0. ь Поэтому /(с) • (Ь - а) ^ 0, т. е. / f(x) dx ^ 0. ■

а

7. Неравенство между непрерывными функциями на отрезке [а;Ь]. (а < Ь) можно итпегрировать. Так, если fi(x) sC /2(.г) при х € [а;Ь].

Jfi{x)dx^fhH

dx.

228

Qj Так как /2(ж) — /i(x) ^ 0. то при а < Ь, согласно свойству 6, имеем

и

f(h(x)-h(x))dx^0.

/^	^Х
' у.-М-	уУ-уЪ^) = }{*)
	:•■,-.;:: ;:;lv ^
	•:■.•:■:•:■:•: : :Т>Ъ: :■.■:■.■:■.-.•:•:•:■:•:■:•

О

Пли, согласно свойству 2,

6 6 6 6

I f₂(x) dx - I f^x) dx ^ 0, т.е. J f_y(x)dx^ I p₂{x)dx. Ш

an а а

Отметим, что дифференцировать неравенства нельзя. 8. Оценка интеграла. Если т и М — соответственно наименьшее и наибольшее значения функции у = f{x) на отрезке [a;b], (а < Ь), то

б т(Ь -а) < Г f(x) dx ^ М(Ь - а). (38.4)

а

Q| Так как для любого х € [а; b] имеем т ^ f(x) $С М, то. согласно

свойству 7, имеем

^J ' 6 6 6

m,dx^ / /(ж) da: ^ / М dx.

о а а

Применяя к крайним интегралам свойство 5, по­лучаем

_{b х} т(Ь-а) <: Г f(x)dx ^ М(Ь-а). Ш

р₁₁₍. yj\ Если /(ж) Jj 0, то свойство 8 ил.погтрирует-

ся геометрически: площадь криволинейной трапе­ции заключена между площадями прямоугольников, основание которых есть [а;Ь], а высоты равны т и М (см. рис. 171).

9. Модуль определенного интеграла не -превосходит интеграла от мо­дуля подынтегральной функции:

б ь

I f(x)dx ^ [\f(x)\dx; a<b.

а а

Q| Применяя свойство 7 к очевидным неравенствам —|/(х)|^/'(ж)^|/(.г)|, получаем

f\fH\dx^ Jf(x)dx^ J\f(x)\

dx.

Отсюда следует, что

и и

I f(x)dx <С f\f(x)\

dx.

10. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная инте­грирования заменена этим пределом, т. е.

//(*)

dt

Я*)

229

Ql По формуле Ньютона-Лейбница имеем:

X

ff(t)dt = F(t)\^x_a=F(x)-F(a).

а

Следовательно.

f(t) dt) = (F(x) - F(a))'_x = F'(x) - 0 = f(x)

Это означает, что определенный интеграл с переменным верхним пре­делом есть одна из первообразных подынтегральной функции.