§36. Геометрический и физический смысл определенного интеграла

Площадь криволинейной трапеции

■^>

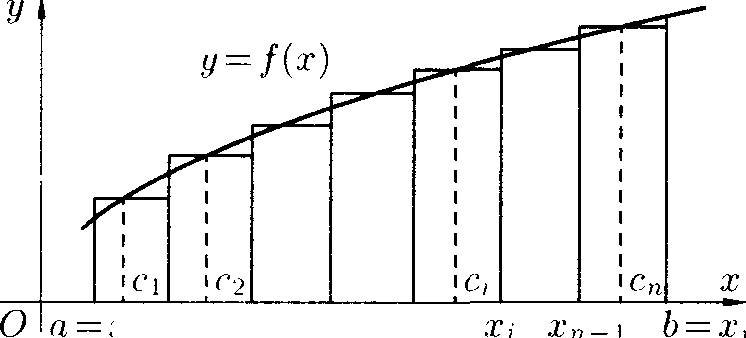
Пусть на отрезке [а: Ь] задана непрерывная функция у = f(x) ^ 0. Фигура, ограниченная сверху графиком функции у = f(x), снизу — осью Ох, сбоку — прямыми х = а и х = Ь, называется криволинейной тра­пецией. Найдем площадь этой трапеции.

222

со -П х-2 :г,_1

Рис. 168

Для этого отрезок [а; b] точками а = хо, х_ь ..., b = х„ (х₀ < xi < ■■■ < х_п) ра­зобьем на п частичных отрезков [хо;Х]], [х\\ хо], ■ ■ ■, [х_п-\:х_п]. (см. рис. 168). В каждом частичном отрезке [x,-_i;x;] ((' = = 1,2,..., гг) возьмем произвольную точ­ку с,{ и вычислим значение функции в ней, т" е. f(a).

Умножим значением функции /(с,-) на длину Дх; = Xi — x,_i соответствующего частичного отрезка. Произведение /(с,-) • Ах, равно площади прямоуголь­ника с основанием Дх,- и высотой /(с,). Сумма всех таких произведений

/(с₁)Дх₁+/(с₂)Дх,+

+ /(с„)Да:_п = ^/(с,-)Д1₁=5„

равна площади ступенчатой фигуры и приближенно равна площади S кри­волинейной трапеции:

£/(<-,-)-Да:,-. ;=1

С уменьшением всех величин Дх, точность приближения криво..тииейной трапеции ступенчатой фигурой и точность полученной формулы увеличи­ваются. Поэтому за гочное значение площади 5 криволинейной трапеции принимается предел 5, к которому стремится площадь ступенчатой фигу­ры S„, когда //. неограниченно возрастает так. что Л — max Дх,- —► 0:

и V

urn

(А->0) i=l

S = lim S„ = lim >J/(с,)Дх,, то есть S = / /(а:)

(fa;.

Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

В этом состоит геометрический смысл определенного интеграла.

[Работа переменной силы

Пусть материальная точка М перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х абсцисса движущейся точки М.

Найдем работу .4 силы F но перемещению точки М вдоль оси Ох из точки х = а. и гонку х. = Ъ (а < Ь). Для этого отрезок [а; Ь] точками а — Хо,

х,\ b = ,г„ (.го < х\ < ■■■ < х„) разобьем на п частичных отрезков

[xo;j'i]. [xi:x-_>], ..., [x„_i;x„]. Сила, действующая на отрезке [x,-i;x,], ме­няется от точки к точке. Но если длина отрезка Д.?;,- = х; — x,_i достаточ­но мала, то сила F на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = с, е [x;_i;x;]. Поэтому работа, совер­шенная этой силой на отрезке [x,;_i:x,-], равна произведению F(c-,) ■ Дх,-. (Как работа постоянной силы F(cj) на участке [а:*-! ;#;]■)

223

Приближенное значение работы А силы F на всем отрезке [а: Ь] есть

A*F{c₁)Ax₁ + F(c₂)Ax₂ + --- + F(c_n)\x_n = £ F(cj)bx,. (36.1)

1=1

Это приближенное равенство те.м точнее, чем меньше длина Л.с,. Поэто­му за точное значение работы Л принимается предел суммы (36.1) при условии, что наибольшая длина Л частичных отрезков стремится к нулю:

Л = lim Y, F(d)&Xi = f F{x) dx

Итак, работа переменной силы F, величина которой есть непрерывная функция F = F(x), действующей на отрезке [а:Ь]. равна определенному интегралу от величины F(x) силы, взятому по отрезку [a: ft].

В этом состоит физический смысл определенного интеграла.

Аналогично можно показать, что путь 5. пройденный точкой за про­межуток времени от t = а до t = ft, равен определенному интефалу от

скорости v(t):

ь

S = I' v(t) dU

<i

масса т неоднородного стержня на отрезке [«; ft] равна определенному нп-

ь

тетрад}' от плотности ~>{х): ni = I ~j(x)dx.