41.3. Вычисление длины дуги плоской кривой

Прямоугольные координаты

Пусть в прямоугольных координатах дана плоская кривая ЛВ. урав­нение которой у -— f(x), где а ^ х ^ Ь.

О V			У	= f(X) M	jAlr,-		i
			Mi-	l/^al^	Ay,
				At,
	M2
	Mxf
	Mo/
	.4. i
о	X(l=fl 3	Д X	2 X,	-1 сг J	1	b	= Xn	X

Под длиной дуги ЛВ понимается предел, к которому стремится дли­на ломаной линии, вписанной в эту дугу, когда число звеньев ломаной не­ограниченно нозрасгает, а длина наи­большего звена ее стремится к нулю. Покажем, что если функция ц = = /(.г) и ее производная у' = /'(■'') непрерывны на отрезке [а:Ь], то кри­вая ЛВ имеет длину, рапную

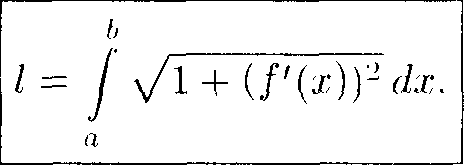
(41.3)

Применим схему I (метод сумм).

1. Точками .го = о., .Г\ г„ = Ь

(хо < -'л < ••• < -г,,) разобьем отре­ зок [о',Ь] па /( частей (см. рис. 183). Рис. 183. Пусть этим точкам соответствуют

точки Л/о = Л, Mi,..., А1„ = В на кривой АВ. Проведем хорды MqMi, AI^M-2, • • ■. M_n^iM,,, длины которых обозначим соответственно через AL\. AL?, ■ ■ ■ ■ AL_n. Получим ломаную А/о-Л/, А/₂... М_п-\ М_п, длина которой равна L_n — AL\ + AL? + ■ ■ ■ + AL_n —

n

= £ ьи.

242

2. Длину хорды (или звена ломаной) AL, можно найти по теореме Пифагора из треугольника с катетами Axj и Ду,-:

Д1, = ■/[Ax_i)² + (Д.(//)², где Дх,- = .т,- - .г,-_1, Д.</,- = /(.Т;) - /(zi-i). По теореме Лагранжа о конечном приращении функции Ду_; = /'(с,) • Да;,, где с,- € (.r,-_i ;.г;). Поэтому

AL, = v'UjO² + №,-ЬД^ = \Д"+ (/'(с,-))²' • Д*,-, а длина всей ломаной МцМ\ ... М„ равна

L„ = ]Г Д1, = ^ \/Щ/'(</))'² ■ Дх,.

(41.4)

/= 1 /= 1

3. Длина / кривой ЛВ, по определению, равна / = lim L_n

max AL,—>0 n

Нш X!! -^i/- Заметим, что при Д£, —> 0 также и Д.т, —> 0 (ALi

шах Л/.,—И) ,—j

= У(Д.г,)-' + (Д.(у,)² и, следовательно. |Д.г,|<Д1,-). Функция уД + СГМР" [1еп])ерывна на отрезке [о; 6], гак как, но условию, непрерывна функция /'(.г). Следовательно, существует предел интегральной суммы (41.4), ко­гда шах Д.г, —> 0:

,i />

I = liin 53 _N/i~+(/'(o))²"A.r₁ = / ^l + (f'(x)y-dx.

max Л/, -->() ^—' ./

(н-->'Х:) ^{,= 1} »

/)

Таким образом. / = / \/] + (f'(x))² dx, иди ^|! сокращенной записи / =

=-- fs/T+uiW'tj-.

а

Если уравнение кривой -Ш задано в параметрической форме (■'• = •'■(/), \lJ = !!(*)■ где¹ r(f) и /;(/) непрерывные (функции с непрерывными производными и .»-(п) = a. -r(.i) = /j, то длина / кривой .Ш находится но формуле

/ = / \Д^Ш+(у'^)У

dt.

(41.5)

Формула (41.5) может быть получена пз формулы (41.3) подстановкой

.г = ./:(0. </•'■ = .v'(t)dt. /'(-О

/(/)'

Пример 41-4- Найти длину окружности радиуса Я. У ■

О Решение: Найдем 4 часть ее длины от точки (0; И) до гочкн (i?;0) (см. рис. 184). Так как /у = х//?² - х²,

о=^й'2-

Рис. 184.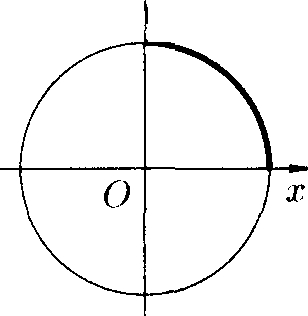

75^"—^ dx = R ■ arc-sin -

2«

Значит, / = 2ttR. Если уравнение окружности записать в параметрическом виде х — Rcost, у = Rs'mt (0 ^ t ^ 2л-), то

2 л-

/ = /" ^(-Rsint)² + (Rcost)² dt = Rtf^ = 2тгД. •

о Вычисление длины дуги может быть основано на применении метода дифференциала. Покажем, как можно получить формулу (41.3), применив схему II (метод дифференциала).

1. Возьмем произвольное значение х G [а; Ь] и рассмотрим неременный отрезок [я:.е]. На нем величина I становится функцией от х, т. е. I = 1(х) (1(a) = 0 и 1(b) = I).

2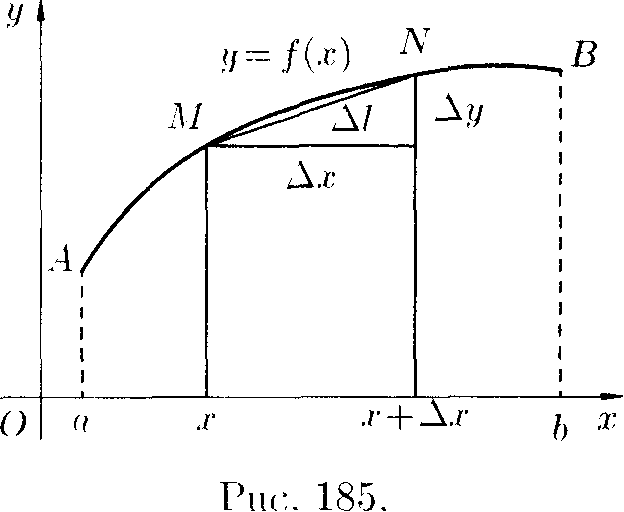 . Находим дифференциал dl функции / = 1(х) при изменении х на малую величину Д,г = dx: dl — l'(x)dx. Найдем l'(x), заменяя бесконечно

малую дугу MN хордой AL стягивающей чту ду­гу (см. рис. 185):

А1, lim —

д.т-»о Ах

1'П

lira

Д.Г-Н)

у/(Ах)* + (Ау)² Ах

lim

Д.г-»0

^{<1 + (g)- = ^:}

Стало быть, dl = sj\ + (у',.]² dx.

_It

² dx

У',

3. Интегрируя dl в пределах от а до b. получаем / Равенство dl ■

1 + y'_r" dx называется формулой дифференциала дуги в прямо­угольных координатах. djl

.</
		у=№/
		/\т^
	м	У^М	<hl
	1 1 1 1	dx	С
о	а х	.г +	dx х

_и>

Ъ

, то

dx

ак как у\.

dl = ^Щ*~+ (dy)².

Последняя формула представляет собой те­орему Пифагора для бесконечно малого треугольника МСТ (см. рис. 186).

Рис. 186.

Полярные координаты

Пусть кривая АВ задана уравнением в полярных координатах г = г(р), а ^ р ^ /1 Предположим, что г(р) и г'(р) непрерывны на отрезке [a;/i].

Если в равенствах х = г соя р. у — г sin у, связывающих полярные и декартовы координаты, параметром считать угол р, то кривую АВ можно

задать параметрически

Тогда

•*v = г'(р)соыр- r(p)sinp,

t iL ^{= r}'(^)^sin ^ + ^ГИ^cos v-

X = 'Г(if) СОЯр,

у = г (if) simp.

244

Поэтому

_{vH)2 + ш2}

= vV(¥>))² + (r(¥>))².

= \/(r'(ip) cos if — г(ф) sin (f)² + (r' (p) sin ip + r(p) cos p)² Применяя формулу (41.5), полумаем

/= /" x/r^+Z¹^.

Пример 41-5- Найти длину кардиоиды г а(1 + cosip).

Рис. 187.

О Решение: Кардиоида г = а(1 + cos;/)) имеет вид, изображенный на рисунке 187. Она симме­трична относительно полярной оси. Найдем половину длины кардиоиды:

-I, = / \/(а(1 + c.osp>))² + («(- sini^))² rf</j = а / \/2 + 2 cos <p> dip =

/■ / ip r ip ip

a / \ 2 • 2 cos^L — oV> = 2«. / cos — «99 = 4« • sin —

4«.

Таким образом, ^/ = 4a. Значит, / = 8a.