§42. Приближенное вычисление определенного

ИНТЕГРАЛА

ь

Пусть требуется найти определенный интеграл / /(.г) d.r or ненрерыв-

ной функции f(j'). Если можно найт первообразную F(j-) (функции /(.г). то интеграл вычисляется по формуле Ньютона Лсйбпипа:

ь

[ f(.r)d.r = F(b)~-F(a).

Но отыскание первообразной функции иногда не(т>ма сложно: кроме того, как известно, не для всякой непрерывной функции ее первообразная выражается через '-элементарные функции. В ттх и других случаях (на­пример, функция у = fi'J') задана графически или таблично) прибегаю! к приближенным формулам, с помощью которых определенный интеграл находится с любой степенью точное-! и.

Рассмотрим три наиболее употребительные формулы приближенною вычисления определенного интеграла формулу нрямоуго. ibihikob. фор­мулу трапеций, формулу парабол (Симпсона), основанные па геометриче­ском смысле определенного интеграла.

•2Г)4

42.1. Формула прямоугольников

Пусть на отрезке [а: Ь], а < Ь, задана непрерывная функция f(x). Тре-

ь

буется вычислить интеграл / f(x)dx. численно равный площади соот-

в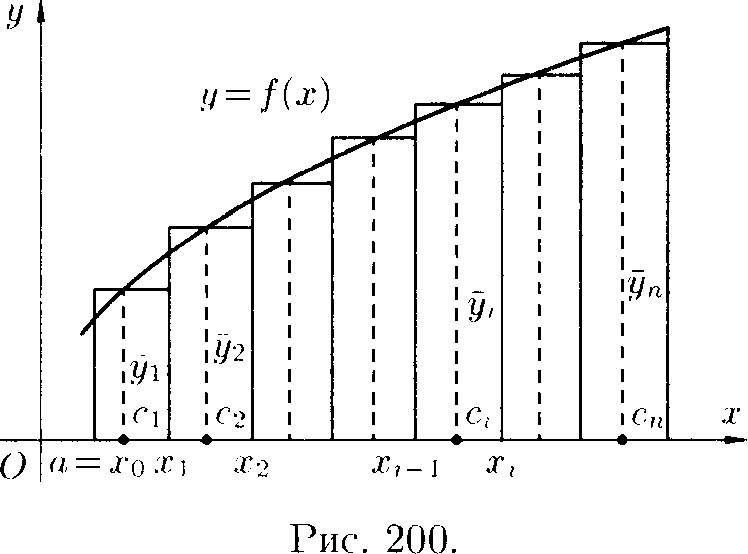 етствующей криволинейной трапеции. Разобьем основание этой трапе­ ции, т. е. отрезок [а; Ь], на п равных частей (отрезков) длины h = —

XI Xj — i

(шаг разбиения) с помощью точек Хо — а, х\, х-2, ■ ■ •, х_п = Ъ. Можно записать, что х\ = = хо + h ■ i, где / = 1,2,..., п (см. рис. 200).

X' 1 "4* X'

Ь = т„

В середине с,- = '"' каждого та­ кого отрезка построим ординату j/j = /(q) графика функции у = f(x). Приняв эту ординату за высоту, построим прямоуголь­ ник с площадью h ■ у,-.

Тогда сумма площадей всех п прямо­угольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого опре­деленного интеграла ь

_/(£^t£i). (42.1)

f(x) dx и Л(г/1 +у->~\ + у»)

- ь~ ^п S~~ f(^Xi~^{l + х}

п

i— 1

d>

Формула (42.1) называется формулой средних прямоугольников.

Абсолютная погрешность приближенного равенства (42.1) оценивает­ся с помощью следующей формулы:

(h - af ■ М-2

24n²

\R„\^

где М-, - наибольшее значение \f"{x)\ на отрезке [а; Ь],

ь , п

'Xi-i +Xi

\R»

_/«*-т?:'т

Отметим, что для линейной функции (/(х) = кх + Ь) формула (42.1) дает точный ответ, поскольку в этом случае f"[x) = 0.

42.2. Формула трапеций

Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обыч­ной.

Разобьем отрезок [а: Ь] на п равных частей длины h = . Абсциссы

точек деления а = xq. Xi,x₂, ■ ■ ■ ,b = х_п (рис. 201). Пусть уо,У\, ■ ■ ■ ,Уп —

255

Рис. 201.

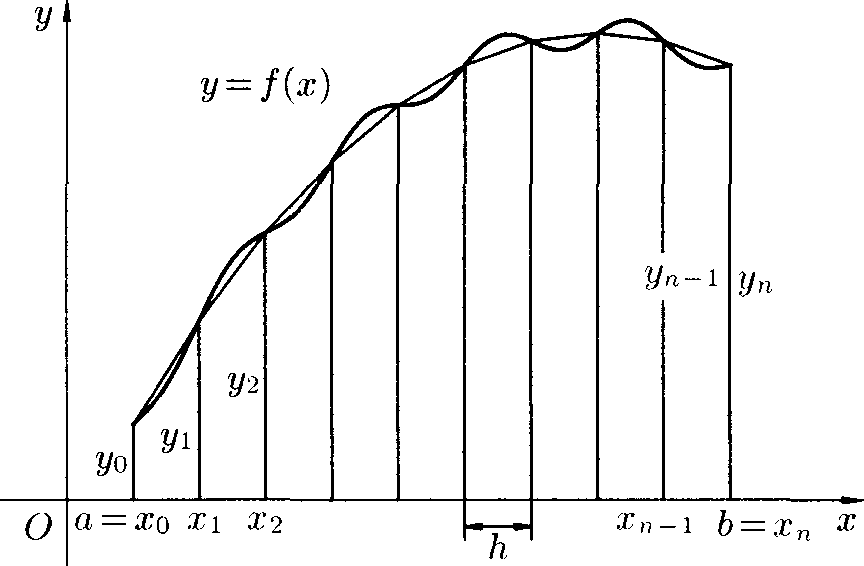
соответствующие им ординаты графика функции. Тогда расчетные фор­мулы для этих значений примут вид x-_t = a+h-i, yi = /(ж;), г = 0.1. 2...., п\

п Заменим кривую у = f(x) ломаной линией, звенья которой соединяют концы ординат у; и y_i+l (i = 0,1, 2,... ,п). Тогда площадь криволиней­ ной трапеции приближенно равна сумме площадей обычных трапеций с основаниями у,-, у,^ i и высотой h — :

У„-1 +Уп __}

_-О-

+ 2/1 +2/2 Н !-?/„-

2 2

6- « (уо + у_п

/(.с) ах ss —-— ■ п Н — ■ h +

//<*>*-^(

42.2)

О

Формула (42.2) называется формулой трапеций.

Абсолютная погрешность R,, приближения, полученного по форму­ ле трапеций, оценивается с помощью формулы \R„\ ^ .J ■ Л/₂, где М-2 = шах |/"(х)|. Снова для линейной функции у = кх + Ь форму-

а ^ х ^ Ь

ла (42.2) - точная.