5. Расчетно-графическая работа к 1 Кинематика точки

Т очка M движется в плоскости x y. Движение точки М в интервале от t₀ до t₂ задано уравнениями: , , где x, y – в метрах [м], t- в секундах [см. табл.1.2), Требуется определить траекторию точки M, а для момента времени t = (c) найти ее положение на траектории, скорость, полное, касательную и нормальную составляющие ускорения, а также радиус кривизны траектории в данной точке.

По полученным данным построить в масштабе траекторию точки, для заданного момента t₁ , найти положение точки на траектории и построить в соответствующих масштабах векторы скорости и ускорения точки.

Таблица 1.2 к расчетно-графической работе К1

№	x = f1(t), м	y = f2(t),м	t0, с	t2, с	t1, с
1	4·cos(π/3)t-1	4sin(π/3)t	0	2	1
2	2sin2(π/6)t-3	-2cos2 (π/6)t	0	3	2
3	5t2+4	3t	0	4	3
4	1+2cos(π/4)t	3sin(π/4)t	0	8/3	4
5	6t	2t2-4	0	3	2
6	5cos(π/6)t	3sin(π/6)t	0	4	3
7	3cos2(π/4)t	3sin2(π/4)t	0	2	1
8	3t2-1	6t	0	5	4
9	4cos(π/3)t+2	4sin(π/3)t-2	0	4,5	3
10	3t	9t2+1	0	2,5	2
11	2е-t + 2	е-t	0	2	1
12	2sin (t) + 1	sin (2t) -2	0	1,2	1/3
13	4sin2 t -2	2cos t +1	0	2	/6
14	sin (t) + cos (t)	sin (t) - cos (t)	0	3	1/6
15	3sin t	2cos (2t)	0	2,5	/6
16	et +е-t	et -е-t	0	0,5	0,5
17	2cos (2t)	3sin2 t + 1-	0	2	/6
18	(1/ cos t) + cos t	(1/ cos t) - cos t	0,1	1,5	/6
19	2cos2 t	2sin (2t) - 1	0	2,5	/6
20	4cos2 t	cos (2t ) +2	0	2,4	/6
21	3cos2 (t)	2cos2 (2t)	0	3	1/6
22	3sin (t/2)	6sin2 (t/4)	0	1,2	1/3
23	2sin2 t	3cos2(2t)	0	2,2	/3
24	4cos2 (t/2)	2sin (t)	0	1,8	1/6
25	2 sin2 t	sin2(2t)	0	1,5	/6
26	2t2	t4+ 2t2+1	0	2	1
27	sin (t2/3) + 1	sin (t2 /3) - 1	0	2,5	1
28	4cos (t2/3)	2/ cos (t2/3)	0	3	1
29	t- 1	t2 _ 2t - 1	0	4	2
30	cos (t2/6) -	2cos2 (t2/6) + 1	0	2	1

Пример 1 выполнения расчетно-графической работы К1

Дано: движение точки задано на плоскости в декартовой системе координат уравнениями движения вида

x= 2t; y=t²+1, (t [c], x,y[м]). (1.39)

Определить уравнение траектории точки, а также для момента времени t = t₁=1с найти и изобразить на чертеже ее скорость и ускорение и их составляющие в декартовой системе координат; радиус кривизны траектории при t = t_{1 .}

Р е ш е н и е.

Уравнения движения (в табл.1.2) являются уравнениями траектории точки в параметрической форме. Чтобы получить уравнение траектории точки в каноническом виде, исключим время t из уравнений (1.39))

,

что соответствует уравнению параболы. Участок траектории показан на рис.1.13. Траекторией будет являться лишь часть параболы при x>0, y>0, положение точки в заданный момент времени t₁ = 1с: x = 2 см; y = 2 см.

Проекции скорости точки на оси декартовой системы координат согласно

; ,

имеют вид: = 2; = 2t, т.е. в рассматриваемом случае в течение всего времени движения перемещение точки происходит по траектории в положительном направлении (проекции скорости на оси координат

= 2. = 2t не меняют своего знака).

Для t = t₁ = 1с: = 2 м/с; = 2 м/с.

Скорость точки: = = ;

для t = t₁ = 1с: = м/с.

Проекции ускорения точки на оси декартовой системы координат согласно

= ; = ,

имеют вид: = 0 м/с²; = 2 м/с²;

для t = t₁ = 1с: = 0 м/с²; = 2 м/с².

Ускорение точки: = 2 м/с². = const

Для определения характера движения (ускоренное или замедленное) точки по траектории следует найти проекцию ускорения на ось, совпадающую по направлению с вектором скорости , т.е. касательное ускорение: = ,

для t = t₁ = 1с: = = 1,41 м/с² .

Из формулы определяем нормальное ускорение

= =1,41 м/с².

Радиус кривизны траектории точки определяем согласно

= м.

0 1 2 3 4 5 м/с

Y₁[м] {см]

,

0 1 2 3 4 5 м/с²

V_x

X ₁[ м].

Рис.1.13

Построение траектории точки, а также векторов скорости и ускорения точки показано на рис.1.13. Вектор скорости должен быть направлен по касательной к траектории, а вектор ускорения необходимо построить двумя способами: по составляющим и , и по составляющим и . При этом векторы ускорений, построенные двумя способами, должны получиться одинаковыми. Векторы скорости и ускорения точки приложены в точке с координатами x = 2 м; y = 2 м.

Ответ: траектория точки – парабола (x>0, y>0); = 5.6 м;

= м/с =2.8 м/с; =2 м/с²; = = 1.4 м/с²; = =1.4 м/с².

Пример 2 выполнения расчетно-графической работы К1

Движение точки М в интервале времени от =0,1 с до =2 с задано уравнениями Определить траекторию точки М, а для момента времени =0,2 с найти ее положение на траектории, скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в данной точке.

Решение.

Заданные уравнения движения являются уравнениями траектории

Рис. 1.14.

точки в параметрической форме. Чтобы получить уравнение траектории точки в каноническом виде, исключим время из заданных уравнений.

Для этого возведем в квадрат обе части уравнений, умножим первое из них на 2 и из полученного результата вычтем второе:

1) Отсюда

Участок траектории точки показан на рис.1.14.

Вектор скорости точки определяется по формуле

Вектор ускорения вычисляется аналогично где

 единичные орты осей и ;  проекции скорости и ускорения точки на оси координат. Проекции скорости на оси координат находим, дифференцируя по времени уравнения движения:

2)

Дифференцируя по времени полученные выражения (2), определяем проекции ускорения на оси координат:

3)

По найденным проекциям определяются модули скорости и ускорения точки

4) 5) .

Проекция ускорения точки на направление ее скорости, т.е. на направление касательной

6) или .

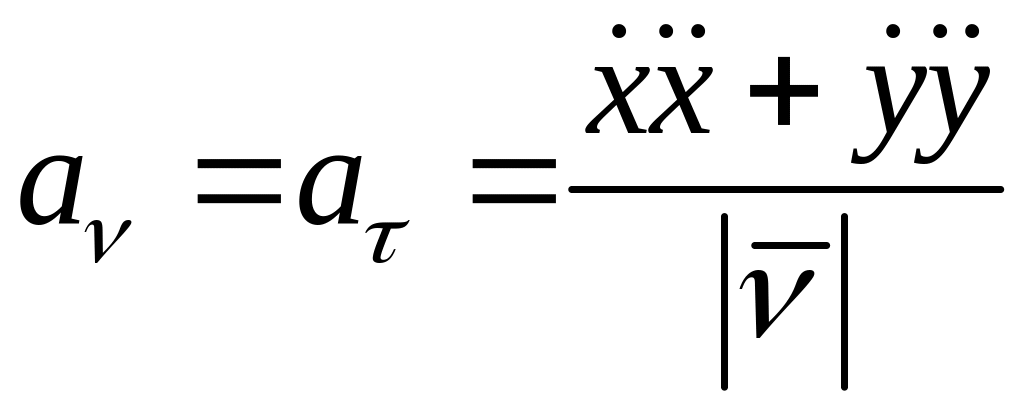Примечание. Если в заданный момент времени скорость точки окажется равной нулю, то правая часть формулы (6) превращается в неопределенность вида и по этой формуле невозможно вычислить касательное ускорение точки. В этом случае можно воспользоваться формулой (2) = (9) для заданного момента времени =0,2 с:

7)

Производная выражает проекцию ускорения точки на направление ее скорости. Знак «+» при означает, что движение точки ускоренное, и направления векторов совпадают;

знак «-»  что движение замедленное, а направления векторов

противоположны.

Модули касательного и нормального ускорений точки соответственно равны:

8)

9) Радиус кривизны траектории в рассматриваемой точке определяется по формуле

Результаты вычислений по формулам ((1 )  (9)) для заданного момента времени =0,2 с:

На рис.1.14 показано положение точки М заданный момент времени. Вектор скорости точки строим в выбранном масштабе по составляющим и , причем этот вектор по направлению совпадает с касательной к траектории . Вектор ускорения строим в масштабе ускорений по составляющим и . Затем откладываем составляющие и . Вектор направляем по касательной к траектории в сторону, противоположную вектору скорости (так как при вычислении получен знак минус), а вектор откладываем перпендикулярно в сторону вогнутости траектории. Контролем правильности решения служит совпадение геометрических сумм и .

Расчет в Mathcad.

Рабочий лист расчета примера 2. Исходные данные:

Участок траектории точки М показан на рис.1.15,а.

Скорость точки:

а б

Рис.1.15.

График зависимости модуля скорости точки от времени показан на рис.1.15,б.

Ускорение точки:

График зависимости модуля ускорения точки от времени показан на рис.1.16,а.

Касательное ускорение: .

Нормальное ускорение: .

Графики зависимости касательной и нормальной составляющих ускорений точки от времени показаны на рис.1.16,б.

а б

Рис.1.16.

Радиус кривизны траектории: .

При получаем