1.2.2. Скорость точки при координатном способе задания ее движения

Даны: кинематические уравнения при координатном способе задания движения точки:

, , (1.2).

Определить: точки М.

Имеем (1.11): , = + + . (1.13)

На основании (1.11) и (1.13) скорость точки, при задании ее движения в декартовой системе координат, определяется как

 +  +  . (1.14)

В (1.14) производные , т.е. коэффициенты при ортах

, , , имеют смысл проекций скорости точки на оси декартовой системы координат, т.е.

,  ,  . (1.15)

Таким образом, скорость точки в данном случае представляет собой сумму составляющих векторов, параллельных осям декартовой системы координат (рис.1.2):

,

где ,  ,  , а ее численное значение (модуль) определяется по формуле

. _. (1.16)

Направление вектора определяется значением направляющих косинусов углов, которые составляет этот вектор с осями декартовой системы координат:

, , . (1.17)

Здесь , ,   углы, которые составляет вектор с осями Ox, Oy и

Oz соответственно.

1.2.3 Скорость точки при траекторном способе задания ее движения

Дано: s = s (t) (1.7). Определить: точки М

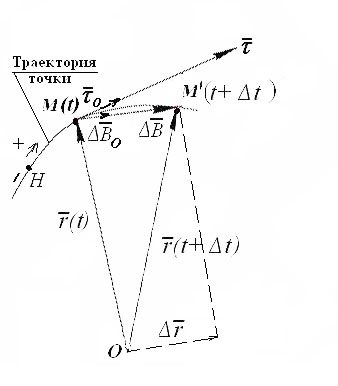
Рис.1.7

В момент времени t положение точки  М, ее траекторная координата  s(t); в момент времени t^’=t+t положение точки M^’,ее траекторная координата s’ (t++t); за бесконечно малый промежуток времени точки t вектор перемещения, , приращение s= s’-s.

За бесконечно малый промежуток времени t = с точностью до величин второго порядка малости, можно считать, что длина хорды равна длине дуги , которую эта хорда стягивает.

Согласно (1.11) и вышесказанному скорость точки можно выразить как

= , где - единичный вектор, характеризующий направление вектора перемещения, т.е. =1 и  , тогда

С учетом = , (1.18^)

где (см. рис.1.7): .

С учетом полученных выражений (1.18^) примет вид:

или . (1.18)

Из (1.18) следует, что проекция скорости точки на ось, касательную к траектории точки, равна

. (1.19)

Очевидно, что .

При  точка движется в положительном направлении отсчета s, а при  в противоположную сторону.

Величину называют также алгебраической величиной проекции вектора скорости точки на касательную. Величина скорости (ее модуль) определяется как:

.

2. Ускорение точки при различных способах задания

ее движения

Определение: ускорением точки, отвечающем данному моменту времени, называется векторная физическая величина, полностью характеризующая изменение скорости точки в данный момент времени как по величине, так и по направлению; изображается закрепленным в данной точке вектором.

1.3.1. Ускорение точки при векторном способе задания

ее движения

Е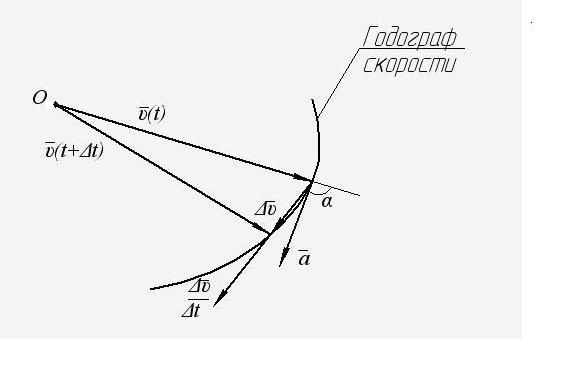 сли откладывать вектор точки в текущие моменты времени t и t₁=t + из некоторой неподвижной точки O, то получим линию в пространстве, называемую годографом скорости (рис.1.8).

Рис.1.8

Очевидно, что приращение скорости за время составит (рис.1.9) .

Отношение этого приращения к промежутку времени , за который оно произошло, определяет среднее изменение скорости точки за рассматриваемый промежуток времени, т.е. . Направление вектора всегда совпадает с направлением приращения скорости . При  0 точка М₁ на траектории приближается к точке М (рис.1.9).

Предельное значение этого изменения скорости за промежуток време

ни , стремящийся к нулю, есть первая производная по времени от скорости точки или вторая производная от радиус-вектора точки, и называется ускорением точки в момент времени t, т.е.

. (1.20)

По своему физическому смыслу ускорение есть скорость изменения

Рис.1.9

скорости точки, и направлено оно по касательной к годографу скорости (рис.1.8). Численное значение ускорения определяется модулем .

Единица измерения ускорения в СИ  метр на секунду в квадрате (м/c²).