1.3.3. Ускорение точки при естественном способе задания ее движения
Ускорение точки можно представить в виде геометрической суммы составляющих, параллельных осям естественного трехгранника :
(1.29)
где
,
,
- касательная, нормальная и бинормальная
составляющие ускорения соответственно.
Для определения ускорения на основании (1.20):
,
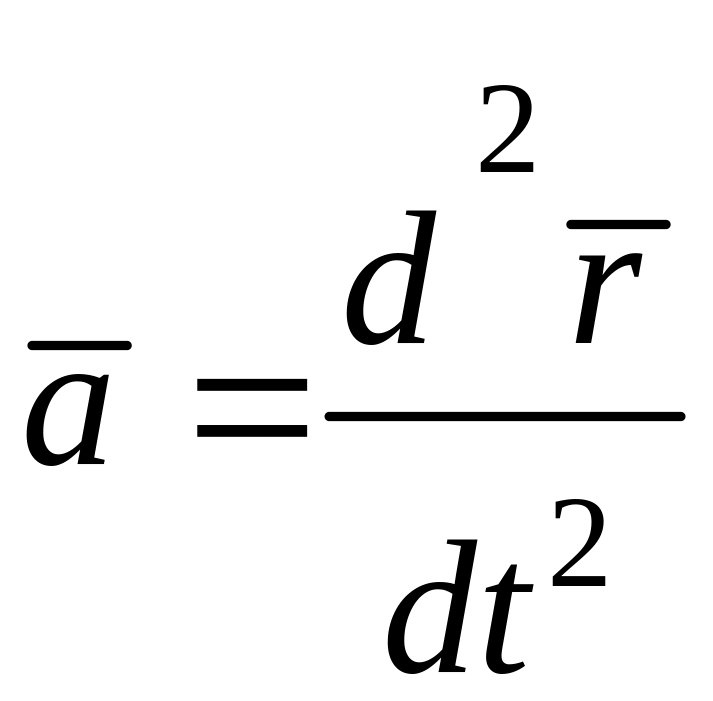с учетом (1.11)
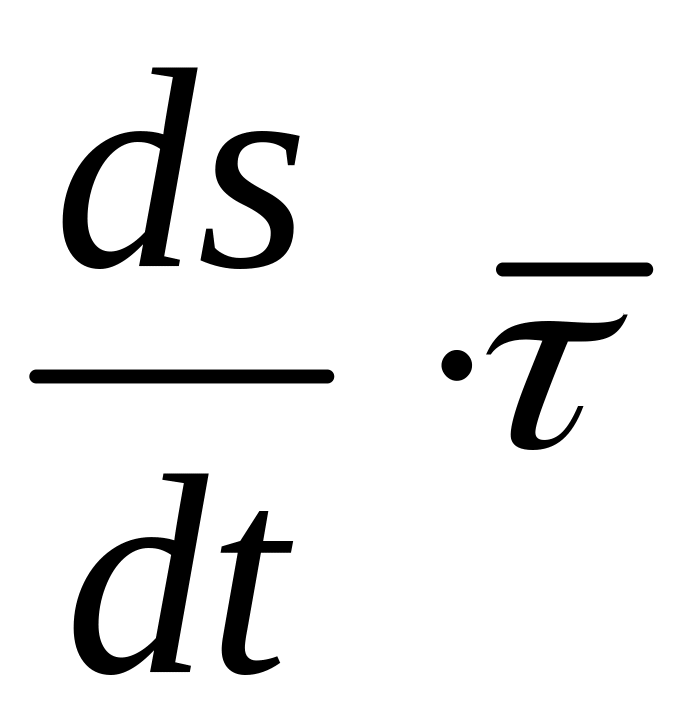, поэтому
.
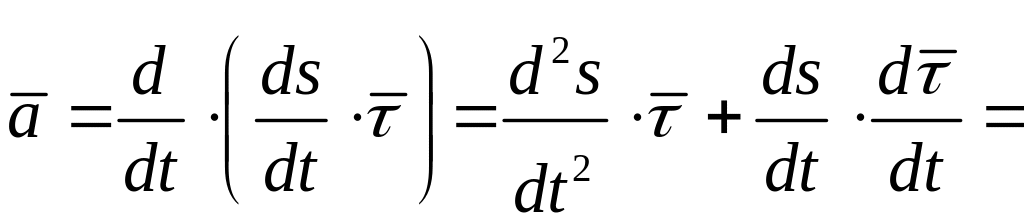
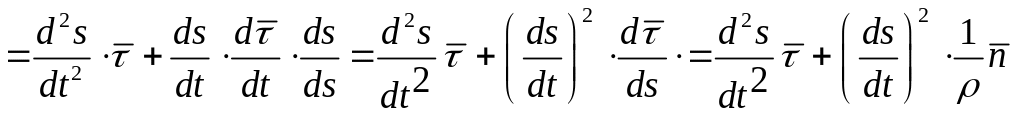Таким
образом ,
(1.30)
Сравнивая полученное выражение для ускорения точки (1.30) с (1.29) видно, что ускорение представляет собой геометрическую сумму составляющих (рис.1.12):
касательной
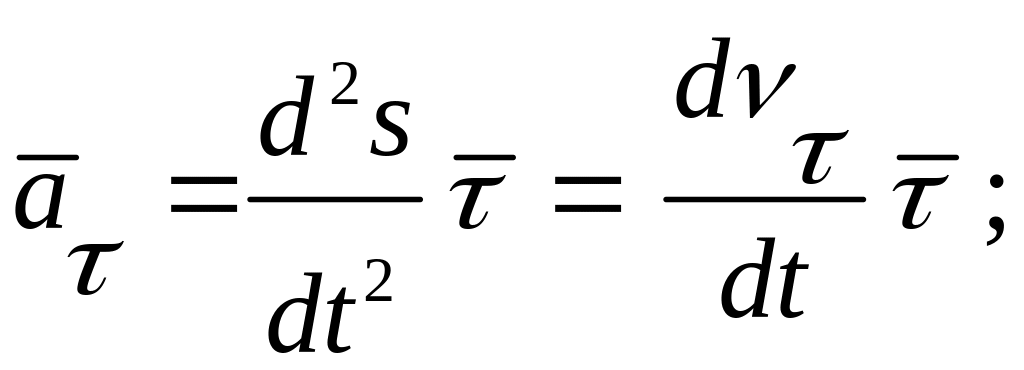
нормальной
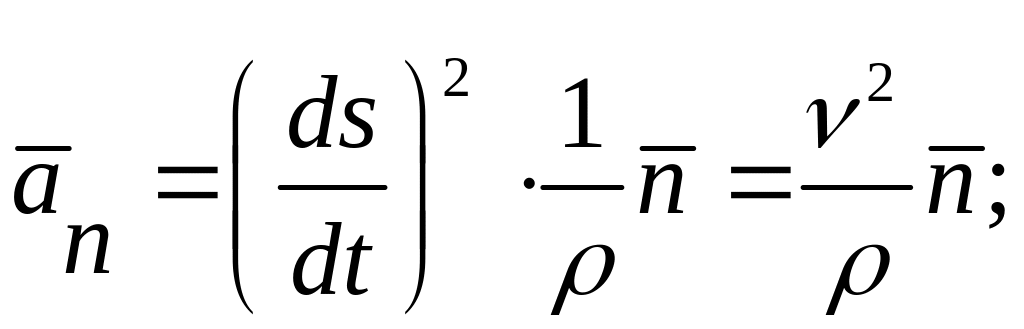(1.31)
бинормальной
(1.32)
Что касается направления вектора
,
определяемого согласно (1.32) (рис.1.12), а
также по отношению к траектории точки
М (рис.1.11), то вектор
лежит в соприкасающейся плоскости (
)
траектории точки М, причем направлен
всегда внутрь вогнутости траектории
движения точки в этой плоскости.
Проекции ускорения на оси траекторной
системы координат (касательную, нормаль
и бинормаль) представлены следующими
выражениями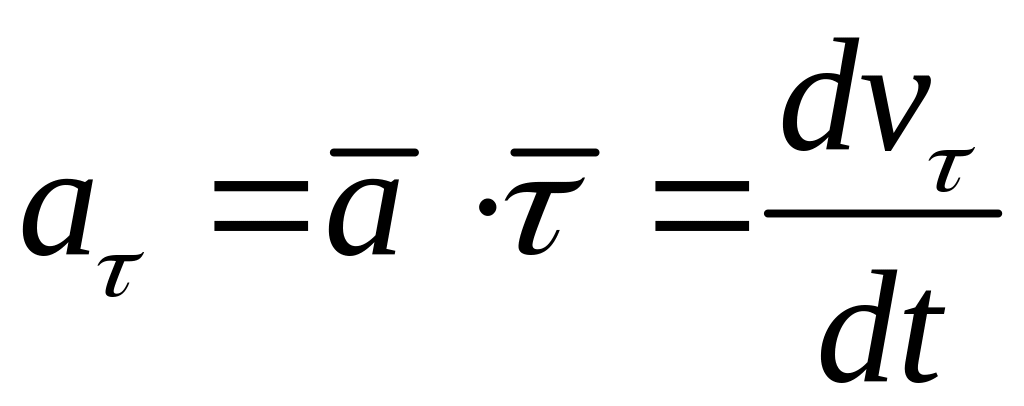 
;
;
(1.33)
.
Модуль проекции ускорения на касательную ось, характеризует изменение скорости по величине, а знак показывает соответствие направления касательной составляющей ускорения направлению единичного вектора , т.е. выбранному положительному направлению отсчета траекторной координаты s.
Значение проекции ускорения на нормаль
всегда положительно и характеризует
изменение скорости только по направлению.
Если рассмотреть движение точки на
криволинейном участке траектории с
постоянной по модулю скоростью (
=
const), то точка будет
иметь ускорение,
н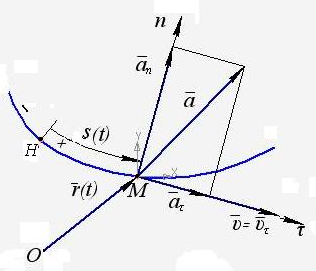
аправленное
по нормали и определяющее изменение
направления век
Рис.1.12
тора
,
так что в этом случае
,
,
т.е.
.
Очевидно,
что
,
,
,
и модуль ускорения
=
.
(1.34)
Заметим, что проекции ускорения на
касательную (
)
и на ось, совпадающую по направлению с
вектором скорости
,
в общем случае равны по модулю, т.е.
.
Характер движения точки по траектории
(ускоренный или замедленный) определяется
исходя из знака
:
-если
>
0, то движение точки ускоренное, при
этом
и
направлены в одну сторону;
-если < 0, то движение точки замедленное, при этом и направлены в противоположные стороны;
При
движение точки равномерное (
),
в этом случае при движении точки по
криволинейной траектории
,
.
Кинематические уравнения движения точки по траектории (закон скоростей и закон траекторных координат)
Дано:
.
Определить:
,
-закон скоростей :
,
откуда
;
;
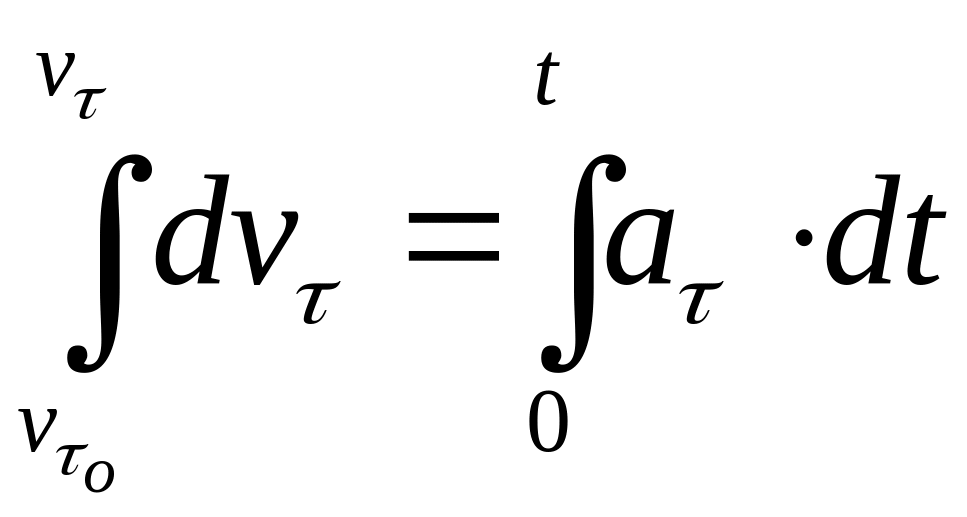. (1.35)
-закон траекторных координат :
,
откуда
;
;
.
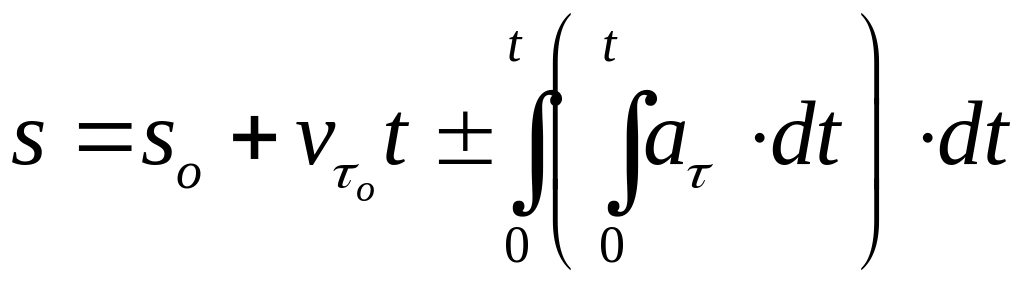(1.36)
Для частного случая равнопеременного движения точки, когда
и
,
из (1.35) и (1.36) соответственно получаем
; (1.37)
.
(1.38)
В зависимости от того, будет ли движение точки равноускоренным или равнозамедленным, формулы для закона изменения скорости (1.37) будут иметь две разновидности, а для закона изменения траекторной координаты(1.38) четыре:
«+» - при равноускоренном,
«-» -при равнозамедленном движении.
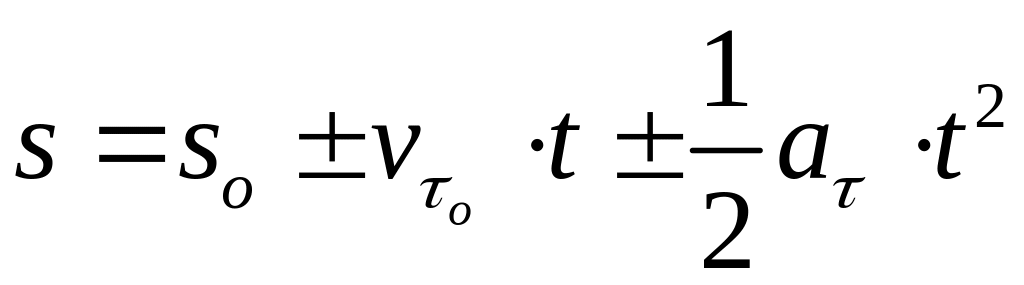« +» перед (
),
если точка движется в положительном
направлении отсчета s, и
« - » перед (
)
в противоположную
сторону.
Кинематические характеристики точки для трех случаев задания ее движения приведены в табл.1.1.
Таблица 1.1 КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТОЧКИ: