1.3.2. Ускорение точки при координатном способе задания ее движения

На основании (1.20) и (1.3) формула для определения ускорения

примет вид (рис.1.2)

=  +  +  , (1.21)

_{а проекции ускорения на оси декартовой системы координат будут}

,  = ,  = ,(1.22)

где составляющие ускорения, параллельные осям координат, определяются как ,  ,  , а численное значение (модуль) ускорения определяется по формуле

. (1.23)

Направление вектора определяется значением направляющих косинусов углов, которые составляет этот вектор с осями декартовой системы координат: , , . (1.24)

Здесь , ,   углы, которые составляет вектор с осями Ox, Oy и

Oz соответственно.

Понятие о сопровождающем (естественном) трехграннике

П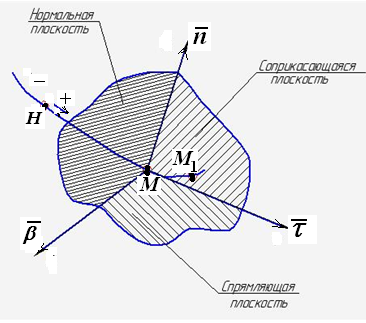 режде чем находить ускорение при траекторном (естественном) способе задания движения точки, введем понятие о сопровождающем трехграннике, определим оси естественной системы координат и ее вектор

Рис.1.10

ный базис, т.е. систему трех единичных векторов, задающих положительное направление этих осей (рис.1.10).

Первая ось траекторной системы координат  ось касательная к кривой (траектории) в данной точке М, положительное направление которой следует принимать в соответствии с выбранным положительным направлением (движения точки по траектории) траекторной координаты s;

обозначается  .

Единичный вектор всегда направлен по касательной к траектории в соответствии с выбранным положительным направлением траекторной координаты s и модуль его равен =1.

Вторая ось естественной системы координат  нормальная ось (нормаль), расположена в соприкасающейся плоскости, перпендикулярна касательной к траектории в точке и направлена в сторону вогнутости траектории движения точки, обозначается  .

Здесь следует напомнить некоторые сведения из дифференциальной геометрии. Если откладывать касательные к траектории и в текущие моменты времени (рис.1.11), то очевидно, что приращение траекторной координаты за время = составит = , а касательная к траек

Рис.1.11

тории за это же время повернется на угол смежности .

Отношение этих приращений за рассматриваемый промежуток времени определяет среднюю кривизну траектории

. (1.25)

Предел этого отношения, когда приращение траекторной координаты, т.е. расстояние между двумя близлежащими точками М и М^’ траектории стремится к нулю, есть производная от по скалярному аргументу s

равен кривизне траектории в данной точке:

(1.26)

где  радиус кривизны траектории в данной точке.

Кроме того, следует учесть, что производная от единичного вектора по скалярному аргументу s есть вектор, перпендикулярный и направлен по нормали к касательной траектории движения точки в сторону ее вогнутости.

Без вывода приводим нужную в дальнейшем зависимость

(1.27):

Единичный вектор , задает положительное направление нормальной оси и равен =1. Вектор лежит в соприкасающейся плоскости, перпендикулярен касательной и направлен в сторону вогнутости траектории к центру ее кривизны в данной точке.

Третья ось естественной системы координат называется бинормальной осью (бинормалью), обозначается. Она перпендикулярна к касательной и нормальной осям, а ее положительное направление совпадает с

единичным вектором бинормали , который определяется как результат векторного произведения единичных векторов и в виде

(1.28)

Таким образом, векторный базис , и определяют положительное направление соответствующих координатных осей в каждой точке траектории. Оси естественной системы координат: касательная  , нормаль  и бинормаль  , построенные в точке M траектории, образуют естественный трехгранник. При движении точки M по своей траектории естественный трехгранник с вершиной в точке M также движется и ориентация его граней и осей, их образующих, изменяется в пространстве.