Кинематика

^{_____________________________________________________________________________________________________}

Кинематика  раздел теоретической механики, в котором изучается механическое движение тел независимо от взаимодействия между ними (с геометрической точки зрения).

Под механическим движением понимают перемещение в пространстве и во времени одних тел относительно других. Те тела, относительно которых рассматривается движение, называются системами отсчета. С системой отсчета связывают систему координат, в которой рассматривают перемещение исследуемого материального тела или системы тел с течением времени. Начало отсчета времени выбирают произвольно.

Задать движение материального тела - это значит иметь возможность однозначно определить положение рассматриваемого материального тела и любой его точки относительно выбранной системы отсчета в любой момент времени.

Вот почему мы начинаем изучение данного раздела с кинематики точки, а потом переходим к изучению кинематики твердого тела. Простейшей моделью материального тела, формой, размерами и вращательным движением которого в условиях рассматриваемой задачи можно пренебречь по сравнению с его поступательным движением  является материальная точка. Абсолютно твердым, или просто твердым, телом называется такое тело (совокупность системы материальных точек), расстояние между любыми точками которого неизменно.

Кинематика точки

Способы задания движения точки

Кинематика точки  раздел кинематики, в котором изучается механическое движение материальной точки и основных ее кинематических характеристик: траектории движения точки, как геометрического места последовательных (с течением времени) положений точки в пространстве относительной выбранной системы отсчета; скорости и ускорения точки.

Существует несколько способов задания движения точки. Сущест-венными среди них являются векторный, координатный и траектор-ный. Кинематические характеристики точки для трех случаев задания ее движения приведены в табл.1.1.

Все три способа взаимосвязаны, т.е. возможен переход от одного способа задания движения точки к другому.

Векторный способ задания движения точки

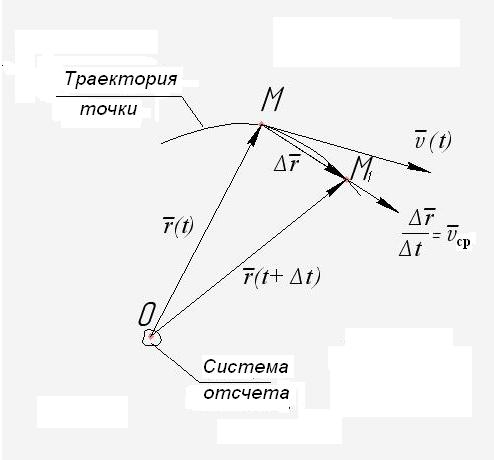Для задания движения точки векторным способом необходимо выразить ее радиус - вектор в виде функции времени относительно выбранной

Рис.1.1

системы отсчета из неподвижной точки О

, (1.1)

Функция предполагается непрерывной и дважды дифференцируемой. Траекторию точки можно определить как годограф ее радиус- вектора (рис.1.1), т.е. геометрическое место концов радиус-вектора , изменяющегося во времени согласно зависимости (1.1). Векторный способ задания движения точки в виду своей простоты в дальнейшем широко используется для определения кинематических характеристик и при других способах задания ее движения.

Координатный способ задания движения точки

Д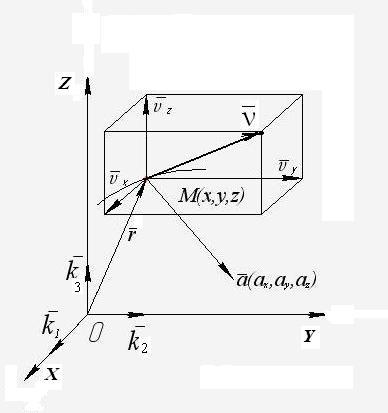 ля задания движения точки координатным способом необходимо ввести прямоугольную декартову систему координат, неизменно связанную с выбранной системой отсчета, с началом в точке O и осями OXYZ (рис.1.2) и дать зависимости изменения координат точки в виде функций времени. Эти зависимости во всех далее рассматриваемых случаях предполагаются непрерывными и дважды дифференцируемыми и называются

Рис. 1.2

кинематическими уравнениями движения точки

, , (1.2)

Зависимости (1.2) одновременно являются и уравнениями траектории точки в параметрической форме, где параметром является время t.

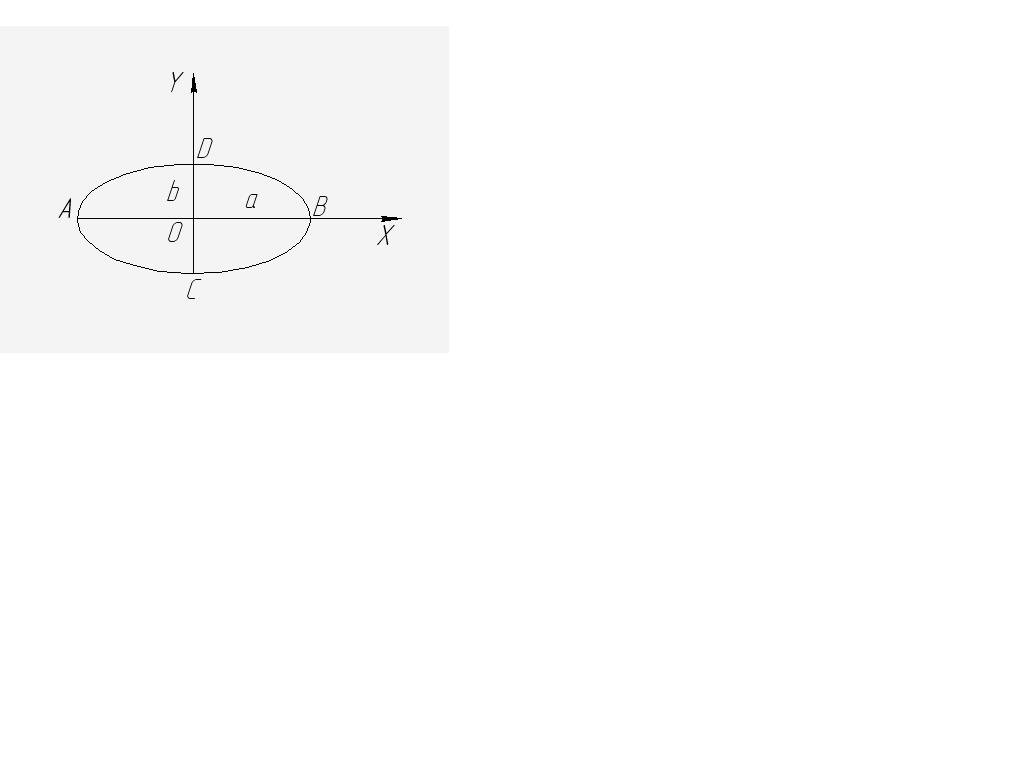
Для получения уравнения траектории точки в каноническом виде, т.е. в форме непосредственной зависимости между координатами x, y, z, из системы уравнений (1.2) необходимо исключить время t. В частном случае задания движения точки на плоскости OXY, например, в виде уравнений движения x = a cos kt, y = b sin kt, z = 0 (параметрическое задание) уравнение траектории точки в канонической форме будет:

, - уравнение эллипса (координат

Рис. 1.3

ные оси совпадают с осями эллипса), большая ось которого АВ = 2а, малая ось СD = 2b , вершины A, B, C, D (рис. 1.3). Следует также заметить, что траекторией точки может быть не вся кривая, описываемая (1.2), а только часть ее, соответствующая реализуемому процессу и времени t (время всегда положительно).

Между векторным и координатным способами задания движения точки существует следующая зависимость (рис.1.1). Проведем из начала декартовой системы координат радиус-вектор точки М и выразим его через координаты точки и орты , , этой системы координат, составляющие ее векторный базис. С учетом уравнений (1.2) имеем: