5.4.2. Нечітка підмножина недомінуємих альтернатив

Розглянемо тепер задачу раціонального вибору альтернатив з множини X, на якій задано нечітке відношення переваги R із функцією належності .

Як ми вже казали раніше, у тих випадках, коли інформація про ситуацію прийняття рішень описана у формі звичайного відношення переваги, раціональним можна вважати обирання максимальних (недомінуємих) альтернатив. Математично така задача зводиться до визначення на поданій множині X підмножини недомінуємих альтернатив.

У цьому розділі ми спробуємо застосувати цей підхід до задач прийняття рішень при нечітко описаному відношенні переваги на множині альтернатив.

Отже, нехай X – звичайна (чітко описана) множина альтернатив й – подане на ній нечітке відношення нестрогої переваги. Hехай, крім того, – відповідне нечітке відношення строгої переваги. Визначимо підмножину недомінуємих альтернатив множини (X, ). Зауважимо, що оскільки вихідне відношення переваги нечітке, то природно чекати, що й відповідна підмножина недомінуємих альтернатив буде нечіткою.

Відповідно визначенню відношення – для будь-яких альтернатив величина є мірою, з якою альтернатива y домінується альтернативою x. Отже, при фіксованому , визначену на X функцію можна вважати функцією належності нечіткої множини всіх альтернатив x, які строго домінуються альтернативою y.

Hехай, наприклад, міра належності альтернативи до цієї множини (відповідно деякому фіксованому y) дорівнює 0,3. Це означає, що домінується альтернативою y зі ступенем 0,3. Легко зрозуміти, що множина "всіх" альтернатив x, які не домінуються альтернативою y є доповненням в X множини . Відповідно визначенню доповнення одержимо, що ця нова нечітка множина описується функцією належності вигляду

, . (5.14)

Якщо, наприклад,  = 0,3, то з мірою 0,7 альтернатива x не домінується альтернативою y. Очевидно, що для визначення в X підмножин "всіх" альтернатив, кожна з яких не домінується жодною альтернативою з X, необхідно взяти переріз нечітких множин виду ( 5.14) за всіма .

О з н а ч е н н я 5.4. Hехай X – множина альтернатив, – подане на ній нечітке відношення переваги. Нечіткою підмножиною недомінуємих альтернатив ми назвемо переріз нечітких множин виду (5.14) за всіма .

Відповідно означення маємо

(5.15)

або

. (5.16)

Значення подає міру, з якою альтернатива x не домінується жодною альтернативою множини X.

Hехай для деякої альтернативи . Тоді може домінуватися іншими альтернативами, але зі ступенем не більше ніж .

Дійсно, при цьому

,

i тодi

.

Визначимо тепер нечітку підмножину альтернатив через функцію належності вихідного нечіткого відношення переваги . Для цього покажемо, що

. (5.17)

Дійсно, нехай – довільна вибрана альтернатива. Введемо множини

, (5.18)

. (5.19)

Користуючись тим, що , для кожного , запишемо (5.17) у такій формі:

. (5.20)

Далі, спираючись на визначення , одержуємо з (5.20):

.

Рівність (5.17) дозволяє описати множину альтернатив, які не домінуються, функцією належності виду

. (5.21)

Вираз (5.21) можемо використовувати для обробки інформації, поданої у формі нечіткого відношення переваги для визначення в X підмножини недомінуємих альтернатив.

Оскільки величина – є мірою "недомінуємості" альтернативи x, то раціональним при поданій нечіткій інформації природно вважати вибір альтернатив, які мають якомога більшу степінь належності до нечіткої множини , тобто тих альтернатив, які дають значення функції найближче до величини

.

Альтернативи, які дають точно цю величину, тобто елементи множини

будемо називати максимальними недомінуємими альтернативами множини .

П р и к л а д 5.5. Hехай у скінченній множині подано нечітке відношення переваги виду

.

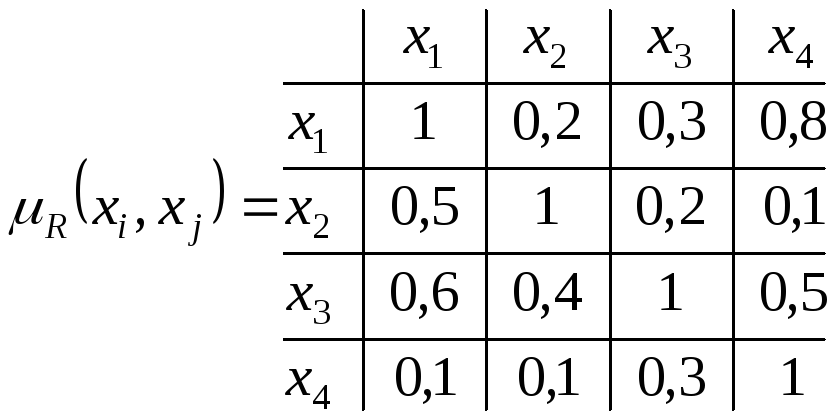Відповідно визначенню отримуємо

,

тоді

.

Звідси бачимо, що найбільшу степінь недомінуємості має альтернатива , й тому вибір її за розв'язком слід вважати раціональним.

О з н а ч е н н я 5.5. Відношення R на X назвемо лінійним, якщо цим відношенням або зворотнім до нього відношенням, пов'язані кожні дві альтернативи поданої множини.

Тобто при лінійності відношення множини X немає альтернатив, що не зрівняні між собою. Для звичайних відношень лінійність означає, що виповнюється рівність

,

де зворотне відношення або інакше, де – доповнення R до , або за допомогою характеристичних функцій

.

У випадку нечіткого відношення однозначно можна визначити лише повну відсутність лінійності: нечітке відношення не є лінійним тоді і тільки тоді, коли знайдуться такі альтернативи , для яких виконується рівність

де – функція належності даного нечіткого відношення. Властивість лінійності у випадку нечіткого відношення можна розуміти більш ширше.

О з н а ч е н н я 5.6. Hехай  – деяке число з інтервалу . Нечітке відношення будемо називати  – лінійним, якщо його функція належності має властивість

(5.22)

Таким чином, якщо нечітке відношення порядку є, наприклад, 0,7– лінійним, то з кожних двох альтернатив одна не гірше за другу зі ступенем не меншим за 0,7.

О з н а ч е н н я 5.6. Hечітке відношення називається сильно лінійним, якщо його функція належності задовольняє умові

, (5.23)

Інакше цю властивість можна визначити таким чином:

. (5.24)

Покажемо, що сильна лінійність еквівалентна умові

, (5.25)

де – відповідне нечітке відношення строгої переваги.

Дійсно, якщо виконується (5.23) відповідно визначенню отримуємо та тобто умова (5.24) також виконана. Якщо виконано (5.24) та , то й тобто виконується і (5.23).

Зміст сильної лінійності можна пояснити таким чином. Якщо, наприклад, альтернативи x та y такі, що x строго краще y зі ступенем 1, то , тобто ні з яким додатним ступенем. Якщо ж , то тобто зі ступенем 1. Якщо ж зі ступенем , то зі ступенем 1 –  виконується перевага . Таким чином, за своїм змістом сильна лінійність значною мірою аналогічна властивості лінійності звичайного відношення.

Сильно лінійні відношення мають такі властивості:

1.

2. Відповідні сильно лінійному відношенню відношення та співпадають.

Дійсно, нехай, для деяких виконано . Тоді з визначення (сильної лінійності) випливає, що , і із визначення отримуємо . У наслiдок симетричності у випадку маємо .

О з н а ч е н н я 5.7. Нечітке відношення переваги ми назвемо слабо лінійним, якщо воно має властивість ,

Приклади нечітких відношень, що є лінійними. Hехай X – множина з 4 елементів.

1. 0,5 – лінійне відношення.

.

2. Сильно лінійне відношення.

.