3.9. Поняття рішення задачі багатокритеріальної оптимізації при заданій перевазі

Розглянемо задачу багатокритеріальної оптимізації

w_i(х)  min, i  I,

х  Х,

де 0 < w_i(x) < 1, i  I і задана перевага на множині функцій цілі w.

Л е м а  3.2. Для кожної допустимої альтернативи х  Х, такої що, 0 < w_i(x) < 1, для i  I, в просторі W  Е^М існує вектор р, який задовольняє співвідношенням:

p = ( p₁, p₂, … p_M ) = { p: p_i > 0,  i  I, }, (3.12)

і число k₀ > 0, таке що альтернатива х  Х задовольняє одночасно М рівностям

p_i w_i (x) = k₀, i  I. (3.13)

Доведення

Оскільки w_i (х) > 0, для i  I, то розділивши обидві частини виразу (3.13) на w_i (х), отримаємо, що

р_i = k₀ / w_i(x) . (3.14)

Але оскільки величини р_i повинні задовольняти умові (3.12) то підставивши в співвідношення вираз для р_i, отримаємо

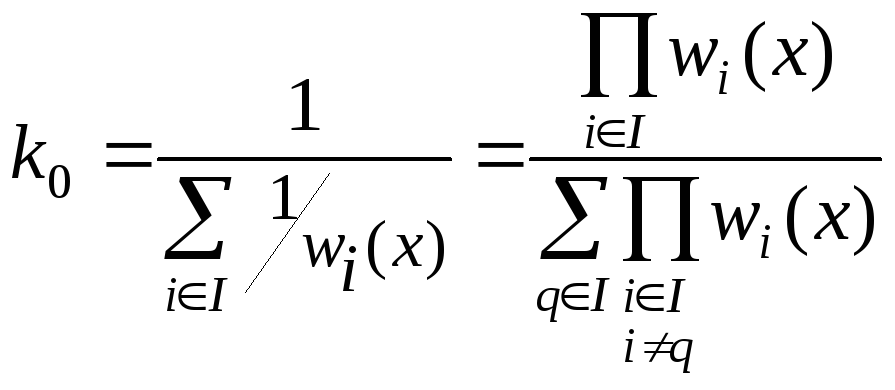, (3.15)

і, відповідно, . (3.16)

Це і доводить лему.

З а у в а ж е н н я. Вираз (3.15), що визначає параметр k₀, є монотонно зростаючою функцією по кожній із змінних w_i(х) на інтервалі (0,1), при цьому k₀  ( 0; 1/М ).

Л е м а  3.3. Якщо для двох нееквівалентних альтернатив х^* та х^** з множини Х вектори р^* і р^** співпадають ( p_i^* = p_i^**, для всіх i  I ), то w_i(х^*) = γw_i(х^**), для всіх i  I і k₀(х^*) = γk₀(х^**), де γ – коефіцієнт пропорційності   1.

Доведення

х^* задовольняє р_i , тобто w_i(х^*) = k₀ (х^*), для всіх i  I,

х^** задовольняє р_i , тобто w_i(х^**) = k₀ (х^**), для всіх i  I,

звідси і .

Якщо тепер врахувати, що p_i* = p_i**, для всіх i  I, отримаємо, що

,

це і доводить лему.

Відмітимо, що напрям, визначуваний вектором р  Р⁺, задається для альтернатив, що знаходяться в позитивному октанті в просторі W значень функції w.

Довільний вектор вагових коефіцієнтів р  Р⁺, що задовольняє умовам (3.12) інтерпретуватимемо як віддавання переваги функції цілі одною перед одною, виражене в кількісній шкалі.

Визначимо напрям, породжений вектором р в просторі W. Задамо цей напрям кутами β_i (i  I) між осями координат і радіус-вектором р.

Тоді

Де e_i = (0, ... , 0, 1, 0, …, 0), орт на вісі w_i, а w^* = {w_i^*} – точка, що знаходиться в просторі W на промені р.

Враховуючи це співвідношення і умову нормування, запишемо систему лінійно-незалежних рівнянь, з яких легко можуть бути знайдені невідомі направляючі косинуси:

.

З іншого боку через лему 3.2, для будь-якої точки w^* виконується система рівностей (3.13) звідки

звідси

Розв’язуючи цю систему, отримаємо таку формулу для направляючих косинусів вектора р.

. (3.17)

Вважатимемо функції цілі рівноцінними, якщо р_i = 1 / M , , тоді направляючи косинуси вектора р в просторі W визначатимуться за формулами:

.

Таким чином, задавання переваг між цільовими функціями в кількісній шкалі за допомогою співвідношення (3.12) вказує напрям пошуку рішень в просторі значень W вибраних перетворень.

Тому під рішенням задачі векторної оптимізації розумітимемо таку компромісну альтернативу, яка належить множині ефективних альтернатив і лежить на заданому напрямі, визначуваному вектором р  Р⁺, в просторі W значень вибраних перетворень функцій.

Якщо для деякої альтернативи x і заданого вектора р  Р⁺ виконується співвідношення p_iw_i(x) = k₀, i  I, то говоритимемо,що альтернатива х лежить на напрямі, визначеному вектором р  Р.

Знайдемо, яке значення параметра k₀ відповідає ефективній альтернативі, що лежить в заданому напрямі, визначуваному вектором р.

Т е о р е м а 3.4. Якщо х₀ – ефективна альтернатива для заданого вектора р  Р⁺ , то їй відповідає найменше значення параметра k₀, при якому система рівностей (3.10) виконується одночасно для всіх i  I.

Якщо за перетворення w_i(f_i(х)) , i  I обрати перетворення виду (3.10), то з врахуванням цієї теореми рішення задачі векторної оптимізації можна визначити таким чином: під рішенням задачі векторної оптимізації для заданого вектора переваг р  Р⁺ розуміється компромісна альтернатива х^к  Х, яка забезпечує однакові мінімальні зважені відносні втрати за всіма критеріями одночасно.