ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Свойства входных функций пассивных цепей. Энергетические функции цепи. Критерии реализуемости двухполюсника по заданной входной функции.

Современная система передачи и обработки информации представляет собой ряд устройств, каждое из которых выполняет определенные операции над сигналами, такие, например, как выделение их из смеси с помехами, разделение сигналов различных источников информации, преобразование формы сигналов и т. д. Все эти операции выполняются с помощью электрических цепей с соответствующими характеристиками. Примерами таких цепей являются различные фильтры с требуемыми характеристиками передачи, корректирующие согласующие цепи, используемые в совокупности с активными элементами, фазовращатели, цепи обратной связи в усилителях, следящих системах, цепи формирования сигналов сложной формы и др.

Важнейшей задачей, возникающей при проектировании радиоаппаратуры, является задача построения электрических цепей с заданными характеристиками – задача синтеза цепей по заданным частотным или временным характеристикам, т. е. обратная задача теории цепей. Результатом решения задачи синтеза является физически осуществимая электрическая цепь, состоящая из элементов с вещественными положительными параметрами, сопротивлений R, емкостей C, индуктивностей L (или взаимных индуктивностей M), в задаче синтеза активных цепей – также и зависимых источников. Задача синтеза имеет неоднозначное решение, поскольку одни и те же заданные характеристики могут быть реализованы несколькими различными цепями. Следует отметить, что не для всякой функции, описывающей заданную характеристику, может быть найдена физически реализуемая цепь, в этом случае задача синтеза вообще не имеет решения.

В зависимости от того, в какой форме задана требуемая характеристика, процесс синтеза может быть разбит на три этапа.

Первый этап заключается в установлении необходимых и достаточных условий, которым должны удовлетворять функции, выражающие заданные характеристики электрических цепей, т. е. условий, характеризующих возможность построения хотя бы одной физически реализуемой цепи с заданными свойствами.

Второй этап сводится к нахождению функции, удовлетворяющей условиям физической реализуемости и с требуемой точностью воспроизводящей заданную характеристику. Часто требуемая характеристика задана в виде таблицы, графика функции или в виде функции, не удовлетворяющей условиям физической реализуемости цепи. В этих случаях возникает задача вос-

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

произведения заданной характеристики (частотной или временной) с требуемой точностью с помощью функций, удовлетворяющих условиям физической реализуемости. Эта задача − задача аппроксимации, относящаяся к области математики и решаемая ее методами.

Третий этап. Необходимо найти электрические цепи, обладающие характеристиками, найденными в результате решения задачи аппроксимации, и выбирать одну из них для практического осуществления, т. е. решение задачи реализации электрической цепи.

Свойствавходныхфункцийпассивныхцепей.

Поведение цепи (в области комплексного переменного р) описывается некоторыми функциями, определяемыми отношением изображения по Лапласу реакции цепи к изображению по Лапласу воздействия при нулевых начальных условиях.

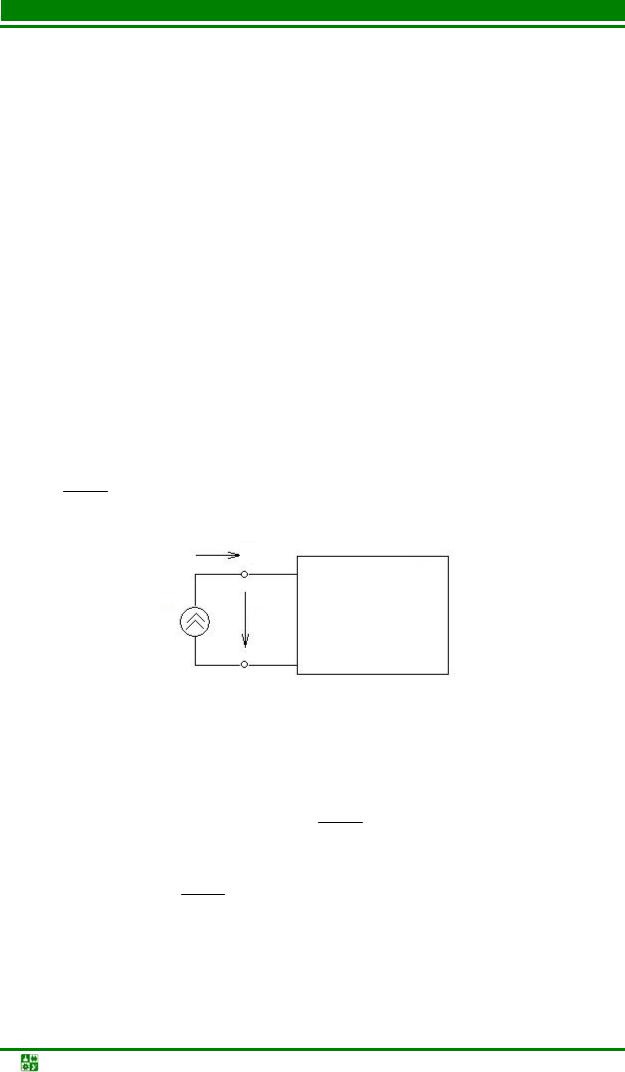
Если к входным зажимам цепи (рис. 36.1) подключить источник тока, то реакцией будет напряжение и функцией цепи будет входное сопротивление

Z (p)= UI ((pp)).

i

n

I U

Рис. 36.1

Если же источником воздействия является напряжение, то функцией цепи будет входная проводимость

Y (p)= UI ((pp)).

Очевидно, что Y (p)= Z (1p).

Поскольку любая сложная цепь может быть рассмотрена как совокупность двухполюсников, рассмотрим входные функции многоэлементных двухполюсников.

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Свойства входных функций пассивных цепей

Если двухполюсник является многоконтурной цепью, то, согласно методу контурных токов,

Z11 (p)I1 (p)+ Z12 (p)I2 (p)+…+ Z1n (p)In (p) = E11 (p),

Z21 (p)I1 (p)+ Z22 (p)I2 (p)+…+ Z2n (p)In (p)= E22 (p),

Zn1 (p)I1 (p)+ Zn2 (p)I2 (p)+…+ Znn (p)In (p)= Enn (p),

где Zik = Rik + pLik + pC1ik – операторное взаимное или собственное (при i = k)

сопротивление контуров; Eii – изображение по Лапласу контурной ЭДС. Решая систему уравнений относительно тока I1(p), получим

Если двухполюсник пассивен, то можно считать контур, в котором находится генератор, первым, а в остальных контурах источников нет, т. е.

E11 (p) = E1 (p), E22 (p) = E33 (p) =…= Enn (p) = 0.

Тогда I1 (p)= 11((pp)) E1 (p), где 11(p) – алгебраическое дополнение,

полученное из определителя (p) вычеркиванием первой строки и первого столбца.

и Y(p) как отношение двух полиномов с целыми степенями р и вещественными коэффициентами:

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Энергетическиефункциицепи.

Если умножить каждое из уравнений системы контурных токов на со-

пряженный ток I k , то для k-го контура получим

Просуммировав левые и правые части n уравнений, получим

где F0, T0, V0 – энергетические функции.

В установившемся синусоидальном режиме (p = jω) правая часть этих уравнений представляет комплексную мощность, отдаваемую источниками.

Энергетическая функция F0 приобретает значение удвоенной мощно-

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Энергетические функции цепи

Таким образом, последние уравнения выражают баланс мощностей в цепи – в левой части имеем активную и реактивную мощность, потребляемую цепью, в правой – полную мощность, отдаваемую источниками

Из физического смысла энергетических функций следует, что они могут принимать только вещественные положительные значения F0, T0, V0 ≥ 0.

Для пассивного двухполюсника матрицы (E) и (I) содержат по одному элементу Е(р) и I(p). Тогда уравнение баланса мощностей принимает вид

Деление на |I|2 можно считать нормированием. При возбуждении двухполюсника током |I| = 1

Поскольку F0, T0, V0 – вещественные неотрицательные при всех возможных р, |I|2 положительна, то:

а) Z(p) вещественно при вещественном р.

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Энергетические функции цепи

Действительно,

Re Z (p)= F0 +T0 Re p +V0 Re 1p =

б) ReZ(p) ≥ 0 при Rep ≥ 0.

Аналогично для Y(p) = 1/Z(p):

а) Y(p) вещественна при вещественном р,

б) ReY(p) ≥ 0 при Rep ≥ 0.

Действительно,

По определению, R(σ,ω) ≥ 0 при σ > 0, поэтому ReY(p) ≥ 0 при Rep ≥ 0. Функции, удовлетворяющие требованиям пп. (а) и (б), называются по-

ложительными вещественными функциями (ПВФ).

Таким образом, входные функции пассивных двухполюсников положительны и вещественны.

Нулями функций двухполюсника являются значения р, при которых

Из этого выражения нельзя непосредственно получить значения p1,2, так как F0, T0, V0 сами являются функциями р. Однако можно сделать следующие выводы.

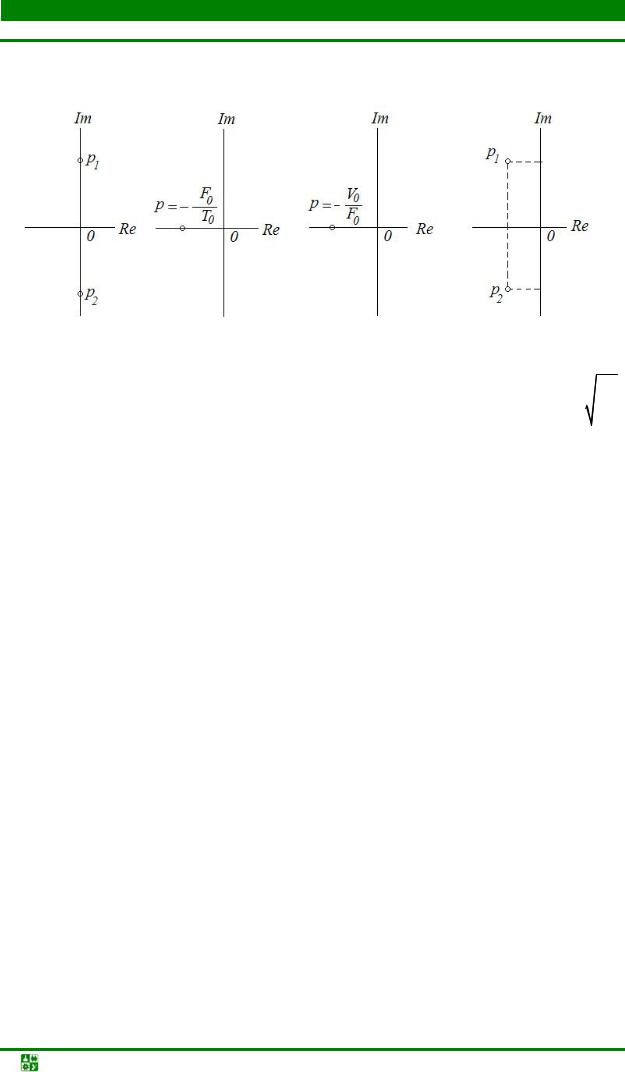
1. Так как F0, T0, V0 – вещественные неотрицательные, то из выражения для p1,2 следует, что все нули Z(p) расположены в левой полуплоскости

(рис. 36.2).

т. е. все нули расположены на мнимой оси (границе левой полуплоскости) (рис. 36.2, а).

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Энергетические функции цепи

т. е. все нули расположены на мнимой оси (границе левой полуплоскости) (рис. 36.2, а).

тельной вещественной оси (рис. 36.2, в).

Критерииреализуемостидвухполюсника позаданнойвходнойфункции.

Выше было показано, что входные функции цепи являются положительными вещественными функциями, следовательно, можно утверждать, что если какая-либо функция имеет подобные свойства, то она может быть реализована в качестве входной функции пассивного двухполюсника.

Для проверки функций используют ряд критериев, основанных на свойствах положительных вещественных функций и связанных:

а) с внешним видом функции; б) с расположением нулей и полюсов;

в) со свойствами полюсов на мнимой оси и вычетов в них; г) с поведением вещественной части функции.

Критерии приведены в порядке возрастающей сложности проверки. Если в последовательном процессе проверки функция не удовлетворяет хотя

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Критерии реализуемости двухполюсника по заданной входной функции

бы одному из критериев, то проверку следует прекратить, поскольку функция уже не является положительной вещественной.

Проверка по внешнему виду функции. Поскольку рациональная функция F(p) вида

должна принимать вещественные значения при вещественном Р, то все коэффициенты an, an–1, ... a0, bm, bm–1, ... b0 должны быть вещественными.

Выше было показано, что F(p) (Z(p) или Y(p) представляют собой отношение определителей, порядок которых отличается не более чем на единицу. Следовательно, высшие степени полиномов M(p) и N(p) так же, как и их низшие степени, не могут отличаться более чем на единицу.

Действительно, при неограниченном возрастании частоты: ω → ∞ (p → ∞) пассивный двухполюсник ведет себя либо как эквивалентная индук-

тивность, т. е. Z(p) → pL, либо как эквивалентная емкость Z (p)→ pC1 , либо

как сопротивление Z(p) → R.

С другой стороны, F (p)= Z (p)→ an pn−m при p → ∞. bm

Следовательно, случай Z(p) → pL соответствует n – m = 1, случай

Z (p)→ pC1 m – n = 1 и случай Z(p) → R соответствует m = n.

Выше было показано, что все нули и полюсы входных функций лежат в левой полуплоскости, т. е. в M(p) и N(p) допустимы сомножители типа

(p + α), (p + α ± jβ) или (p2 +α2k ), где α, β, αk неотрицательны. Отсюда следу-

ет, что все коэффициенты an, an–1, ... a0, bm, bm–1, ... b0 должны быть неотрицательны. Кроме того, при перемножении указанных сомножителей никакие члены не могут быть исключены путем вычитания, а значит, в полиномах M(p) и N(p) никакие степени не могут быть пропущены между высшей и низшей степенями, кроме случая, когда отсутствуют все четные или все нечетные степени (LC-цепи).

Условие положительности и вещественности коэффициентов полиномов является необходимым, но не достаточным, чтобы функция F(p) была положительной вещественной. Необходимо также, чтобы нули функций M(p) и N(p) лежали в левой полуплоскости (в крайнем случае, на мнимой оси).

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Критерии реализуемости двухполюсника по заданной входной функции

Полиномы с вещественными коэффициентами, все нули которых находятся в левой полуплоскости, называются строгими полиномами Гурвица. Если полином имеет простые нули на мнимой оси, то он называется модифицированным полиномом Гурвица. Таким образом, положительная вещественная функция должна представлять собой отношение полиномов Гурвица. Для того чтобы установить, является ли заданный полином полиномом Гурвица, существует несколько критериев, например, Рауса, Найквиста. Чаще всего используется критерий Гурвица.

Пусть полином L(p) является числителем или знаменателем функции F(p). Представим L(p) в виде суммы двух частей: L(p) = m(p) + n(p), где m(p) – четная часть от L(p) содержащая все четные степени p: p0, p2, p4, ..., а n(p) − нечетная часть от L(p) со всеми нечетными степенями p: p, p3, p5, ... Показано [5], что полином L(p) является полиномом Гурвица, если при разложении отношения его четной части к нечетной (или обратное ему со старшей степенью в числителе) в цепную дробь получаются только положительные коэффициенты.

Пример 1. Проверить, является ли полином

L(p) = 36p5 + 12p4 + 48p3 + 10p2 + 15p + 1

полиномом Гурвица.

Решение. Образуем отношение нечетной части полинома к четной, поскольку старшая степень нечетная.

Проведем один шаг деления числителя на знаменатель:

36 p5 + 48 p3 +15 p 12 p4 +10 p2 +1

Обозначим новую функцию ψ1 (p)= m((p)), степень числителя которой n1 p

выше степени знаменателя на единицу, и осуществим следующий шаг деления:

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Критерии реализуемости двухполюсника по заданной входной функции

в которой все коэффициенты положительны, следовательно, полином L(p) – полином Гурвица.

Пример 2. Проверить, является ли полином

L(p) = 2p5 + 3p4 + 7p3 + 7p2 + 6p + 1

Поскольку в разложении имеются отрицательные коэффициенты, полином L(p) не является полином Гурвица.

Свойства вычетов в полюсах на мнимой оси. Возможны три случая расположения полюсов на мнимой оси: 1) p = 0 (начало координат), 2) p = ∞, 3) p = ± jωi.

Разложение функции F (p)= MN ((pp)) на простые дроби в общем случае записывается следующим образом:

где k∞, k0, ki, kj – вычеты функции F(p) в простых полюсах в бесконечности, в нуле, на мнимой оси и на вещественной оси. Для определения kj-вычета в простом полюсе p = pj умножим обе части последнего разложения на (p – pj) и определим их при p → pj. В этом случае в правой части все члены, исключением kj, исчезают. В результате получаем

lim M ((p))(p − p j )= k j .

p→p j N p

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Критерии реализуемости двухполюсника по заданной входной функции

Если функция F(p) имеет общий множитель p в знаменателе, то она имеет полюс при p = 0 и вычет в этом полюсе

Поскольку все коэффициенты полиномов M(p) и N(p) положительные вещественные числа, то вычет k является вещественным положительным.

Функция F(p) имеет полюс в бесконечности, если степень полинома числителя на единицу выше полинома знаменателя. Один шаг деления полиномов дает вычет k∞ в p = ∞, который, так же как и k0, вещественный положительный.

Если функция F(p) имеет полюсы на мнимой оси p = ± jωi, то знаменатель N(p) имеет сомножители (p − jωi )(p + jωi ) = (p2 + ωi2 ). В разложении

на простые дроби появляются члены вида

которые также являются вещественными положительными числами.

Проверка неотрицательности вещественной составляющей функ-

ции на мнимой оси. Для того чтобы функция F(p) была положительной вещественной, необходимо иметь ReF(p) ≥ 0 при Rep ≥ 0, т. е. для проверки F(p) нужно найти ее вещественную часть и убедиться, что она нигде не будет отрицательной при изменении p = jω в пределах от –∞ до +∞.

Запишем F(p) как отношение полиномов, имеющих четные и нечетные части числителя и знаменателя:

где m1 и m2 − четные, n1 и n2 − нечетные части числителя и знаменателя.

ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ

Критерии реализуемости двухполюсника по заданной входной функции

Знаменатель F(p) − четная функция, первая скобка числителя также четная, а вторая − нечетная, поэтому для p = jω

быть отрицательным, то очевидно: для того чтобы ReF(jω) ≥ 0, необходимо

A(ω2 )= (m1m2 − n1n2 ) p= jω ≥ 0 при –∞ ≤ ω ≤ ∞. Полином A(ω2) − четный, следовательно, можно рассматривать интервал 0 ≤ ω ≤ ∞ вместо –∞ ≤ ω ≤ ∞.

Введя переменную x = ω2, получим

A(ω2) = A(x) = Cnxn + Cn – 1xn – 1 + ... + C1x + C0 = k(x – x1)(x – x2)...(x – xn),

где xi = ωi2 − нули полинома A(x) = A(ω2).

Знак полинома A(x) зависит от знаков множителей, определяемых его нулями. Вещественный отрицательный нуль всегда дает положительный множитель. Также положительный множитель дает пара комплексных со-

пряженных нулей. Действительно, если xi = a ± jb, то (x – a + jb)(x – a + jb) = = (x – a)2 + b2 ≥ 0 при 0 ≤ x ≤ ∞.

Очевидно, что отрицательный множитель может давать только любой положительный нуль нечетной кратности. В случае положительного нуля четной кратности пара отрицательных одинаковых множителей дает положительный множитель.

Таким образом, для неотрицательности ReF(jω) необходимо и достаточно, чтобы полином A(x) не имел положительныx корней нечетной кратности. Проверку данного условия проводят разными методами: Будана, Труди, Штурма и др. Чаще всего используется теорема Штурма, позволяющая установить число вещественных положительных корней уравнения A(x) = 0, заключенных в любом интервале a ≤ x ≤ b (a и b не являются корнями полинома A(x). Согласно теореме Штурма, число вещественных положительных корней полинома в интервале a ≤ x ≤ b равно разности |na – nb|, где na − число перемен знака в ряде функций Штурма при нижнем a и nb − верхнем b пределах переменного x. Определение таким образом количества корней есть при-