ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский государственный университет науки и технологий им. академика М.Ф. Решетнева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ОТЦ лекции.pdf

Скачиваний:

1071

Добавлен:

17.03.2015

Размер:

6.1 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 1516 / 3516 17 18 19 20 21 22 23 24 25 26 27 28 > Следующая >>>

Xi = Xiept , Hki (p)=

Xi = Xiept , Hki (p)=

Xi =Xie pt

Единичная функция и переходная характеристика цепи. Интеграл Дюамеля. Импульсная функция и импульсная характеристика. Интеграл наложения. Связь между переходной и импульсной характеристиками. Связь интеграла Дюамеля с интегралом наложения.

Рассмотренные выше методы расчета переходных процессов практически не пригодны при сложных формах входных сигналов. В этом случае применяют метод наложения, который заключается в разложении заданного входного воздействия на подобные слагаемые более простой формы, для которых легко найти отклик цепи.

Определив отклик цепи на каждую элементарную составляющую, и суммируя эти отклики, находим отклик цепи на все сложное воздействие.

Отдельные составляющие целесообразно выбирать такими, чтобы они были простыми математически, и расчет откликов, вызываемых ими, был бы не сложен. Элементарные составляющие и вызываемые ими отклики выражают с помощью двух функций: а) единичной функции (единичного скачка); б) импульсной функции (дельта функции).

Единичнаяфункцияипереходнаяхарактеристикацепи.

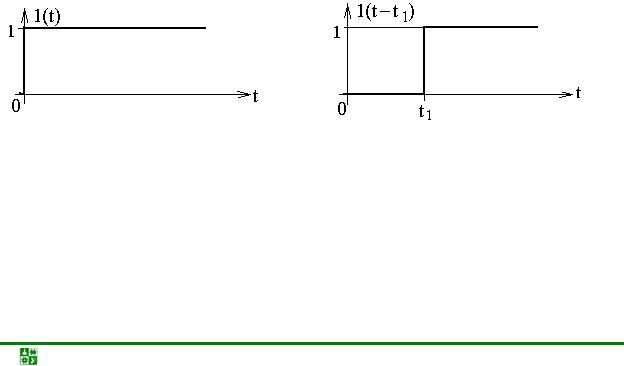
Единичную функцию определяют как функцию времени, равную нулю при t < 0 и равную единице при t > 0 (рис. 23.1, а):

при

t < 0,

1(t −t1 )

при

< t ,

1(t )=

при

t > 0,

при

> t1.

l(t – t1)

l(t)

Рис. 23.1

С помощью единичной функции процесс включения напряжения любой формы e(t) = f(t) на вход цепи в момент времени t = 0 может быть представлен в виде произведения 1(t) f(t). Это произведение равно нулю при t < 0 и равно f(t) при t > 0.

Основы теории цепей. Конспект лекций

-220-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Единичная функция и переходная характеристика цепи

Если входной сигнал подается на цепь не в момент t = 0, а с запаздыванием на t1 (рис. 23.1, б), то его следует записать с помощью единичной функции с запаздывающим аргументом 1(t – t1) f(t).

Отклик цепи на единичную функцию называется переходной характеристикой цепи и обозначается h(t) (единичную функцию можно получить на входе цепи включением в момент t = 0 или t = t1 источника с напряжением 1 В).

Если воздействие запаздывает на некоторое время, то на такое же время запаздывает и отклик цепи. Если воздействие увеличивается в а раз, то во столько же раз увеличивается отклик цепи. Размерность переходной характеристики цепи равна отношению размерностей выходной и входной величин. При внешнем воздействии, заданном в виде единичной функции напряжения, и отклике, являющемся тоже напряжением на каком-либо элементе цепи, переходная характеристика оказывается безразмерной величиной, численно равной выходному напряжению. Если же определяется ток в цепи, то переходная характеристика имеет размерность проводимости и называется пере-

ходной проводимостью.

Для определения переходной характеристики необходимо рассчитать переходный процесс в цепи при нулевых начальных условиях при включении на вход единичной функции напряжения. Таким образом, переходная характеристика является функцией времени и определяется схемой цепи и величиной параметров элементов.

ИнтегралДюамеля.

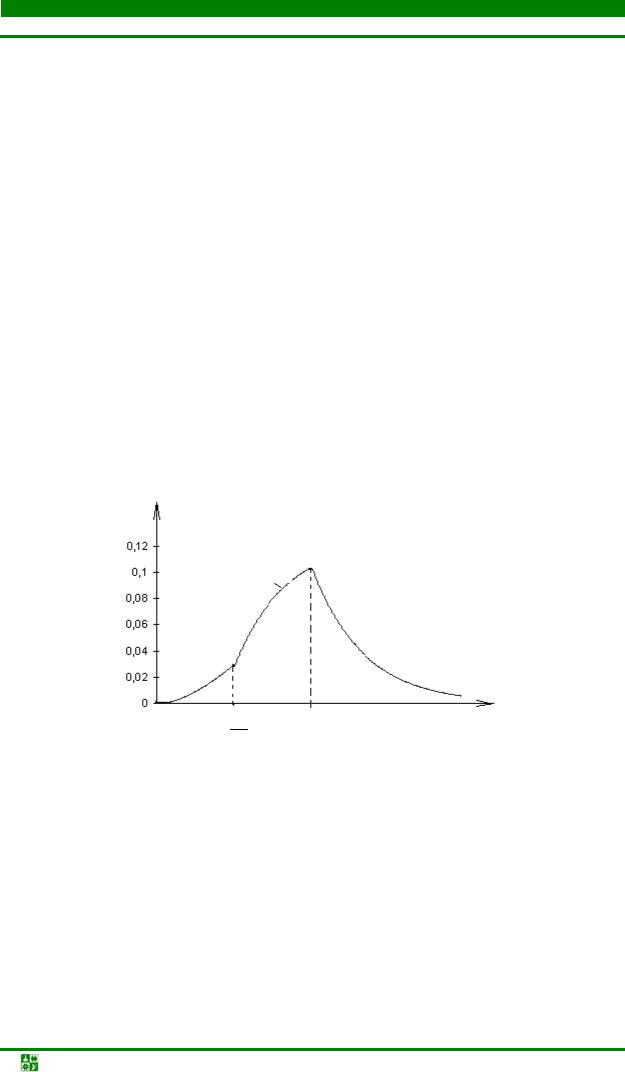
Пусть требуется найти ток в пассивном линейном двухполюснике, переходная характеристика которого известна, при включении на вход источника ЭДС сложной формы (рис. 23.2). Начальный запас энергии к моменту включения ЭДС считаем равным нулю.

е(t)

∆е2 ∆еk

∆е1

е(0)

					t
0
	τ1 τ2	τ3		τk

			t


			Рис. 23.2

Основы теории цепей. Конспект лекций

-221-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Интеграл Дюамеля

Выберем произвольно фиксированный момент наблюдения t и рассчитаем переходный ток к этому времени. Очевидно, что величину тока в этот момент определяет вся кривая входного напряжения от t = 0 до момента наблюдения t. В связи с этим введем новое обозначение текущего времени τ, изменяющегося в пределах 0 ≤ τ ≤ t, и в дальнейшем будем различать e(t), i(t) как функции момента наблюдения t и e(τ) и i(τ) как функции текущего времени τ.

Заменим плавную кривую e(τ) ступенчатой. Это дает основание считать, что в момент времени τ = 0 включается постоянное напряжение e(0)1(t), воздействующее на цепь в течение всего интервала времени от нуля до ∞. Затем через промежуток времени τ1 воздействует e1, затем вступает через τ2 e2 и т. д. Тогда

e(t ) ≈ e(0)1(t )+ e11(t − τ1 )+ e21(t − τ2 )+…+ ek1(t − τk )+…+ en1(t − τn ) =

= e(0)1(t )+ ∑ ek1(t − τk ).

k =1

Под влиянием каждого скачка напряжения возникает переходный процесс, начинающийся в соответствующий момент τ. Под влиянием составляющей e(0)1(t) в цепи появится составляющая тока i(t) = e(0)h(t), поскольку отклик на единичную функцию есть переходная характеристика. Через τ1 под

воздействием e11(t – τ1) в цепи появится составляющая тока i1 =			e1h(t – τ1),
так как e1 воздействует в промежутке времени t – τ1.
В последующий момент времени τ2		вновь происходит скачкообразное
изменение напряжения на величину e2,		которое вызовет вновь составляю-
щую тока	i2 = e2h(t – τ2).		ek вызовет
Аналогично найдем, что в момент τk скачок напряжения
ток ik =	ekh(t – τk).

На основании метода наложения искомый переходный ток будет равен сумме составляющих, найденных для момента t, т. е.

i(t)=e(0)h(t)+Δe1h(t −τ1)+Δe2h(t −τ2 )+…+Δekh(t −τk )+…+Δenh(t −τn )=

=e(0)h(t)+∑ ekh(t −τk ).

k=1

Для того чтобы получить выражение тока, соответствующее плавно изменяющемуся входному напряжению, необходимо число скачков увеличивать до бесконечности (n → ∞), промежутки времени уменьшать до бесконечно малой величины dτ. Величину каждого скачка напряжения de можно представить в виде произведения скорости изменения напряжения de/dt на продолжительность этого промежутка dτ, т. е. de = e′(τ)dτ.

Основы теории цепей. Конспект лекций

-222-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Интеграл Дюамеля

e(t)

I1(p)

I3(p)

I2(p)

(Em = 10 В)

рС

τи

Рис. 23.3

Сумма в пределе перейдет в интеграл и для фиксированного момента времени значение тока будет

i(t )= e(0)h(t )+ ∫e′(τ)h(t − τ)dτ.

Полученное выражение носит название интеграла Дюамеля. Используя теорему свертки функций, можно получить еще одно выра-

жение интеграла Дюамеля:

i(t )= e(0)h(t )+ ∫e′(t − τ)h(τ)dτ.

Пример 5. Для электрической цепи, приведенной в примере 1, рассчитать отклик на входной импульс (рис. 23.3).

Решение. Рассчитаем переходную характеристику цепи как отклик на единичную функцию на входе. При нулевых начальных условиях изображение переходной характеристики – изображение тока в индуктивной ветви – можно определить по закону Ома:

H (p)= I

(p)=

Uab (p)

I1 (p)Zab (p)

, I

(p)=

p(R1

+ R2 + Zab (p))

+ pL

R2 + pL

(R + pL)

Zab (p)=

R2 + pL

R2 + pL +

(R + pL)pC +1

Основы теории цепей. Конспект лекций

-223-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Интеграл Дюамеля

H (p)=

(R2 + pL)

+ pL

((R2 + pL)pC +1)(R2 + pL)

p R1 + R2 +

(R + pL)pC +1

60 10−7 p3 +1210 10−4 p2 +80 p

Перейдем от изображения к оригиналу по теореме разложения:

(p)

)epkt

f (t ) i=i

i=i ∑

(p)

F2′(pk )

k=1

где pk – корни F2(p), в нашем случае F2(p) имеет корни p = 0, p1 = –680, p2 = –19480.

F1 (p) =1; F2 (p) = 60 10−7 p3 +1210 10−4 p2 +80 p;

		F′(p)= 3 60 10−7 p2 + 2 1210 10−4 p +80;
		2
При p = 0 F1(0) = 1;			F2′ =80;
При p1	= –680,	F′(p ) = 76,2;
		2	1
При p2	= –19480,	F2′	(p2 )= 2196

Таким образом, h(t) = 1,25·10–2–1,3·10–2e–680t+ 4,56·10–4e–19480t.

Соответствующий график h(t) приведен на рис. 23.4.

h(t), Сим

t, мс

Рис. 23.4

Основы теории цепей. Конспект лекций

-224-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Интеграл Дюамеля

Проверим правильность расчета переходной характеристики. При t = 0 h(0) должна быть равна нулю, так как переходная характеристика представляет собой ток через индуктивность при нулевых начальных условиях (на основании закона коммутации ток в индуктивности скачком измениться не может). Действительно, h(0) 0. При t → ∞ в цепи устанавливается стационарный режим, ток

i3	=		1		, h(∞)= 0,0125 = i3ПР.
		R1	+ R2
				+ R3

Рассчитаем отклик цепи на входной сигнал.

На интервале			0 ≤ t ≤		τи e = kt ,
					2	11
	Em
где k =		и	′	(τ)= k .

	τи		e11

Представим переходную проводимость в общем виде

h(t ) = A0 + A1ep1t + A2ep2t ,

где A0 = 1,25·10–2, A1 = –1,3·10–2, A2 = 4,56·10–4.

В течение промежутка времени от 0 до τ2и ток в индуктивности

i3 (t )= e(0)h(t )+ ∫e′(τ)h(t − τ)dτ.

Поскольку е(0) = 0, то первый член в выражении для искомого тока отсутствует и тогда

t E

(t−τ)

i3 (t )= ∫e′(τ)h(t − τ)dτ = ∫ τ

A0 + A1e

A2e

dτ =

p t е

− p τ

p t

− p

τ+ A e

∫

τ+ A e

∫

dτ

τи

0 ∫

A ep1te− p1τ

A ep2te− p2τ

A τ+

−p

A t −

A ep1t

A ep2t

−

Основы теории цепей. Конспект лекций

-225-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Интеграл Дюамеля

На интервале времени от τи до τи е12(t) = Em,			e′	(τ) = 0 . Кроме того,
		2	12
	τи	2			Em
при t =		входное напряжение скачком изменяется на величину			Em	.
при t =		входное напряжение скачком изменяется на величину			2	.
	2				2

Следовательно,

τи

(t )=

p (t−τ)

(t−τ)

∫

A + A e 1

+ A e 2

dτ+

τи

A0 +

A1e

p1(t−τ)

+ A2e

p2(t−τ)

τ.

+ ∫e12′ (τ)

τи

(t )=

2 E

(t−τ)

p (t−τ)

dτ+

∫

A e 1

A e

t −

τи

A e p1te− p1τ

A e p2te− p2τ

τи

τ+

−p

p t−

τи

t−

τи

A1e

+ A2e

τи

p1 t−

p2 t−

= Em

τи

A1ep1 t−

A2e p2 t−

−

A1ep1t

−

A2ep2t

−p τ

−p

−p τ

−p

− τ2и +

τ2и + 0 =

В момент времени t = τи входное напряжение скачком уменьшается до нуля, что эквивалентно включению постоянной ЭДС обратной полярности и величиной, равной Em. Следовательно, при t > τи отклик цепи необходимо рассчитывать из выражения

Основы теории цепей. Конспект лекций

-226-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Интеграл Дюамеля

τи

(t )=

(t−τ)

p (t−τ)

dτ+

− E h(t − τ

∫

+ A e

A e

t −

τи

p1 t

τи

t−

τи

p1 t−

−

A1e

= E

−p

p2 t−

A ep1t

A e p2t

A e

(t−τ

)

(t−τ

)

−

− A

− A e 1

− A e

−p2τи

−p1τи

−p2τи

График зависимости тока в индуктивной ветви от времени при заданном входном сигнале приведен на рис. 23.5 (для случая τи = 3/|p1|).

i(t), А

i(t)

τи τи

Рис. 23.5

Импульснаяфункцияиимпульснаяхарактеристика.

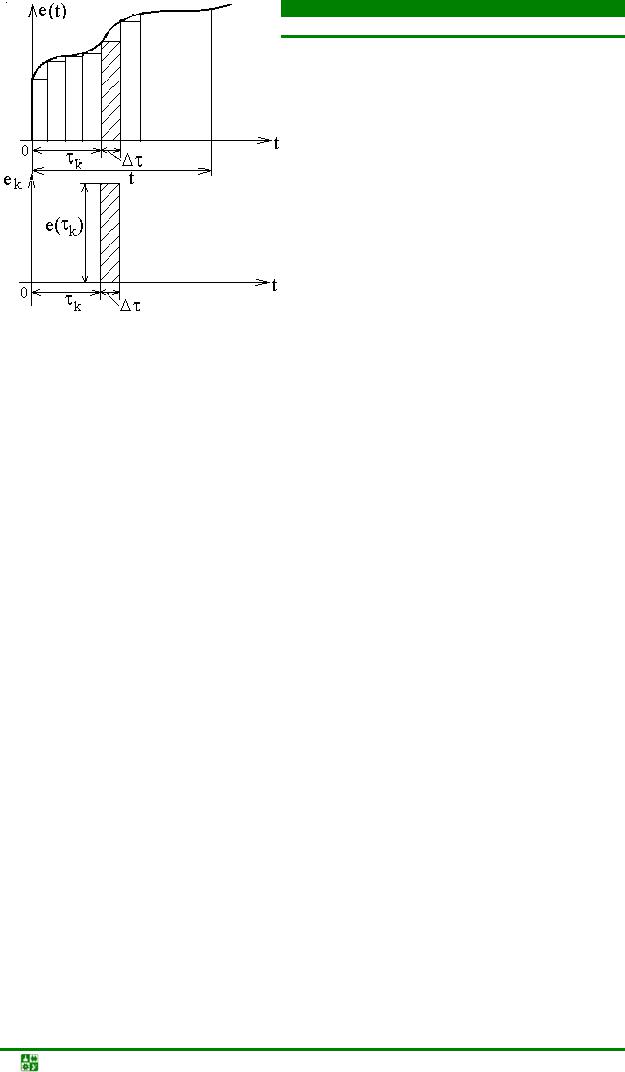
Введем функцию, определяющую прямоугольный импульс длительностью t, высотой 1/ t и площадью S = 1 (рис. 23.6).

	0	при	t < 0, t > t,
	1
δ(t, t )=	1	при
			0 < t < t.
	t
	t

Основы теории цепей. Конспект лекций

-227-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Импульсная функция и импульсная характеристика

δ(t, ∆t)

t

			t
1	0		t
	0

		∆t

Рис. 23.6

Такой импульс получается из двух единичных функций, смещенных одна относительно другой на длительность импульса:

δ(t,	t )=	1	1(t )−	1	1(t − t )=	1(t )1(t − t )	.
		t		t
						t

Наибольший интерес представляет предельный случай прямоугольного импульса, когда его длительность стремится к нулю ( t → 0), а высота – к бесконечности (A = 1/ t → ∞):

lim	δ(t,	t )	= lim	1(t )1(t − t )	= δ(t ).
				t
t→0			t→0

Эта функция называется импульсной функцией и обозначается δ(t). Ее часто называют также дельта-функцией или функцией Дирака. Импульсная функция обладает следующими свойствами:

1)равна нулю при t < 0 и t > 0, т. е. δ(t) = 0 при t ≠ 0;

2)бесконечно велика в точке t = 0: δ(0) = ∞,

3)кроме того,

∞

∫ δ(t )dt =1.

−∞

Если импульсная функция отлична от нуля не в момент t = 0, а в момент τ, т. е. запаздывает на время τ, то она записывается с запаздывающим аргументом δ (t – τ). При этом сохраняется основное свойство функции

∞

∫ δ(t − τ)dt =1.

−∞

Основы теории цепей. Конспект лекций

-228-

[отклик]

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Импульсная функция и импульсная характеристика

Поскольку импульсная функция получена предельным переходом от единичной функции, следовательно, она является производной от единичной функции.

δ(t )=1′(t )= d1dt(t ) .

Из последнего выражения следует и обратное соотношение:

1(t )= ∫ δ(t )dt.

−∞

Важнейшим свойством дельта-функции является фильтрующее свойство, записываемое в виде интегральных соотношений

∞	∞
∫ f (t )δ(t )dt = f (0)	и ∫ f (t )δ(t − τ)dt = f (τ),
−∞	−∞

где f(t) – произвольная непрерывная функция.

Подынтегральная функция в последней формуле равна нулю всюду, кроме точки t = τ. Функция f(t) в этой точке равна f(τ). Тогда f(τ) можно вынести за знак интеграла, а интеграл будет равен единице в силу свойства импульсной функции:

∞	∞
∫ f (t )δ(t − τ)dt = f (τ) ∫ δ(t − τ)dt = f (τ).
−∞	−∞

Таким образом, интеграл от произведения импульсной функции и любой непрерывной функции равен значению непрерывной функции при том значении переменной интегрирования, при котором аргумент дельтафункции обращается в нуль.

Для определения отклика цепи на сложное воздействие оказывается достаточно знать отклик цепи на дельта-функцию, который называется им-

пульсной характеристикой. Ее можно определить так:

g (t )= Y S(t ) ,

где S = δ(t) – воздействие; Y (t) – отклик. Импульсная характеристика = [воздействие][t].

Основы теории цепей. Конспект лекций

-229-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Импульсная функция и импульсная характеристика

Если воздействие увеличивается в а раз, в силу линейности во столько же раз возрастает и отклик. Если воздействие запаздывает на t1, то на такое же время запаздывает и отклик.

Интегралналожения.

Рассмотрим применение импульсной характеристики для расчета отклика цепи на сложное воздействие. Как и в предыдущем случае, найдем ток в цепи при воздействии входного напряжения e(t) (рис. 23.7).

e(t)

				t
	0			t
		τk	∆τ



			t
ek			t

е(τk)

0 τk ∆τ

Рис. 23.7

Аппроксимируем e(τ) последовательностью прямоугольных импульсов en(t) малой длительности Δτ:

(t)=e(τ

) 1(t −τ

)−1(t −τ

−Δτ)

=e(τ

)Δτ

1(t −τk )−1(t −τk+1 )

Δτ

τk = k Δτ, при

Δτ → 0

e(τk ) = e(τ)dτδ(t − τ).

Каждый отдельный прямоугольный (элементарный) импульс с площадью e(τ) dτ δ(t – τ) вызовет ответный отклик в виде составляющей тока

dik(t) = e(τ)g(t – τ)dτ,

где g(t – τ) – значение импульсной характеристики в момент наблюдения t при воздействии импульса на цепь в момент τ.

Основы теории цепей. Конспект лекций

-230-

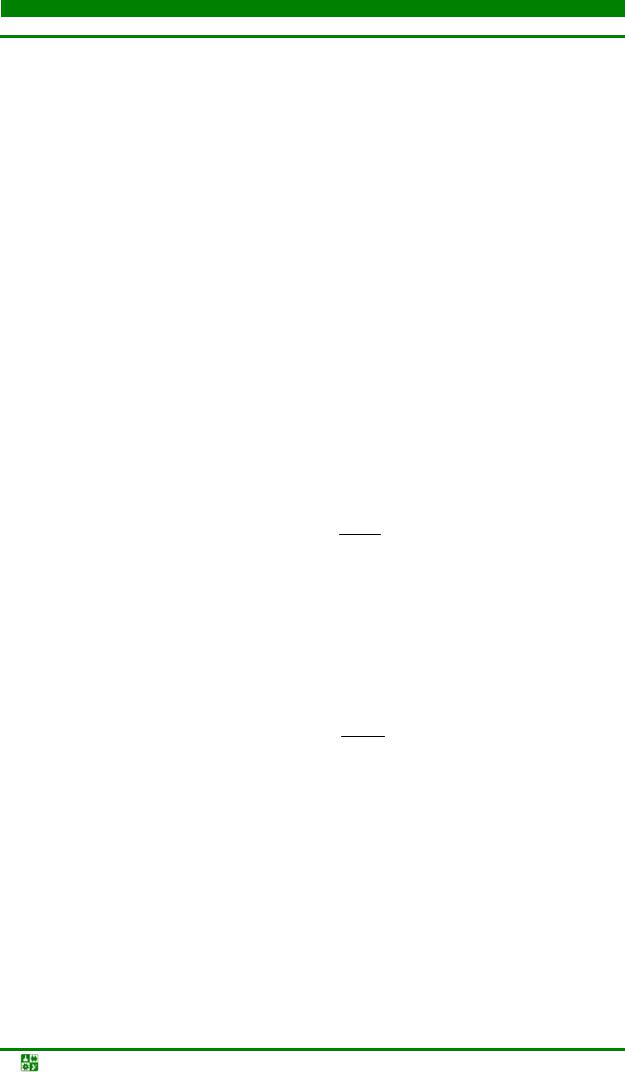
ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Интеграл наложения

Результирующий отклик на все воздействие получим, используя принцип наложения, суммируя бесконечно малые составляющие di(t), вызванные последовательностью бесконечно малых по длительности прямоугольных импульсов напряжения:

i(t )= ∫e(τ)g (t − τ)dτ.

Полученный интеграл называется интегралом наложения. Используя теорему свертки, получим еще одну форму интеграла наложения

i(t )= ∫e(t − τ)g (τ)dτ.

Связьмеждупереходнойиимпульснойхарактеристиками.

Поскольку h(t) и g(t) описывают одну цепь, то, очевидно, они жестко связаны. Выше было показано, что импульсная функция представляет собой производную от единичной функции:

δ(t )=1′(t )= d1dt(t ) .

Отклик цепи на единичную функцию является переходной характеристикой h(t), а так как в линейных цепях следствия находятся в тех же соотношениях, что и вызывающие их причины, то отклик цепи на воздействие импульсной функции должен быть производной отклика единичной функции, т. е. импульсная характеристика g(t) должна быть производной от переходной характеристики h(t):

g (t )= h′(t )= dhdt(t ).

Связь между характеристиками g(t) и h(t) можно получить также, рассматривая отклик цепи на воздействие скачка напряжения Em1(t). При таком воздействии отклик цепи i(t) = Emh(t).

С другой стороны,

t	t
i(t )= ∫Em (t − τ)g (τ)dτ = Em ∫g (τ)dτ,
0	0

откуда

Основы теории цепей. Конспект лекций

-231-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Связь между переходной и импульсной характеристиками

′	(t )=	dh t
h	(t )=		∫
		dt	0

h(t)

h(0)

h1(t)

h2(t)

h(0)

g (τ)dτ = g (t ).

h1(t)

h(0) 1(t)

		t
0		t
0	Рис. 23.8
	Рис. 23.8

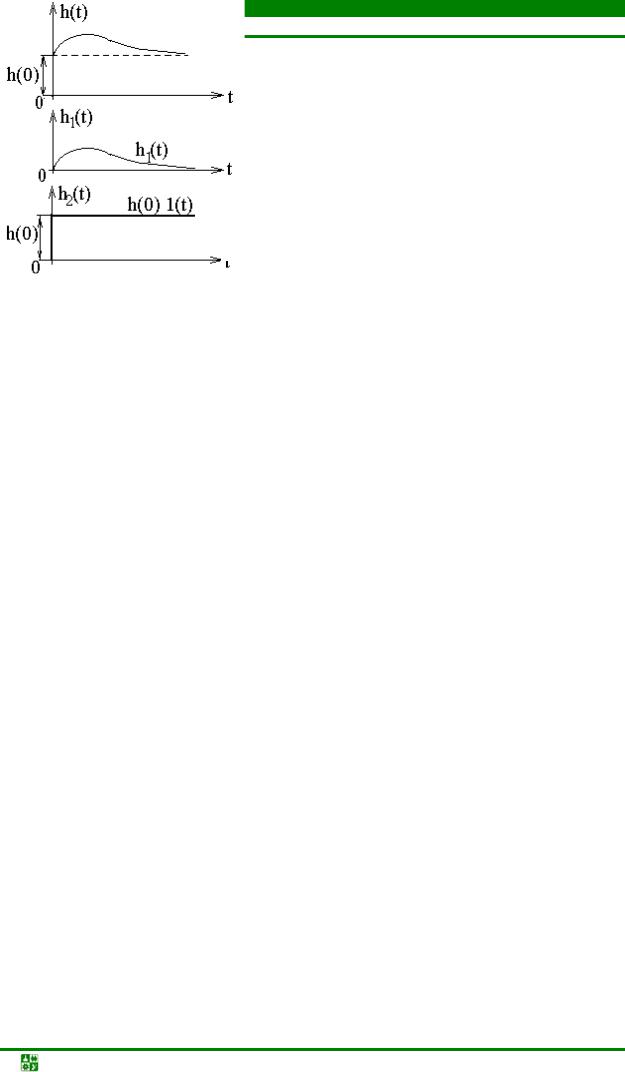
Выражение связи между импульсной и переходной характеристиками цепи несколько отличается в случае, когда переходная характеристика h(t) не равна нулю при t = 0 (рис. 23.8).

h(t) = h1(t) + h2(t) = h1(t) + h(0)·1(t)

тогда

g (t) = h′(t) = h1′(t )+ h(0) δ(t ).

Заменив переходную характеристику суммой двух функций h1(t) и h2(t) = h(0), представляющую собой скачок величиной h(0), возникающий при t = 0, получим импульсную характеристику, в которой этот скачок учтен производной второй функции h(0) · δ(t). Так как функции h(t) и h1(t) подобны при всех значениях t, кроме t = 0, то их производные одинаковы во всех точках, кроме скачка при t = 0.

СвязьинтегралаДюамелясинтеграломналожения.

Подставив выражение для импульсной характеристики в интеграл наложения, получим

t	t	t
	′	(τ)dτ+ h(0)∫e(t − τ)δ(τ)dτ.
i(t )= ∫e(t − τ)g (τ)dτ = ∫e(t − τ)h		(τ)dτ+ h(0)∫e(t − τ)δ(τ)dτ.
0	0	0

На основании фильтрующего свойства импульсной функции

Основы теории цепей. Конспект лекций

-232-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Связь интеграла Дюамеля с интегралом наложения

∫e(t − τ)δ(τ)dτ = e(t ).

Тогда

t	t	(t − τ)h	(τ)dτ.
∫e(t − τ)g (τ)dτ = e(t )h(0)+ ∫e		(t − τ)h	(τ)dτ.
		′
0	0
Таким образом,
t		t
e(0)h(t )+ ∫e′(τ)h(t − τ)dτ = e(t )h(0)+ ∫e(t − τ)h′(τ)dτ.
0		0
Интеграл Дюамеля		Интеграл наложения

Пример 6. Для электрической цепи, приведенной в примере 1, рассчитать ток в индуктивной ветви с помощью импульсной характеристики при входном напряжении e(t) (рис. 23.3).

Решение. Ранее была определена переходная характеристика

h(t ) = A0 + A1ep1t + A2ep2t ,

где A0 = 1,25·10–2, A1 = –1,3·10–2, A2 = 4,56·10–2.

Найдем импульсную характеристику как

g (t )= h′(t )= dhdt(t ) = p1A1ep1t + p2 A2ep2t =8,9e−680t −8,9e−19480t .

График импульсной характеристики приведен на рис. 23.9

Основы теории цепей. Конспект лекций

-233-

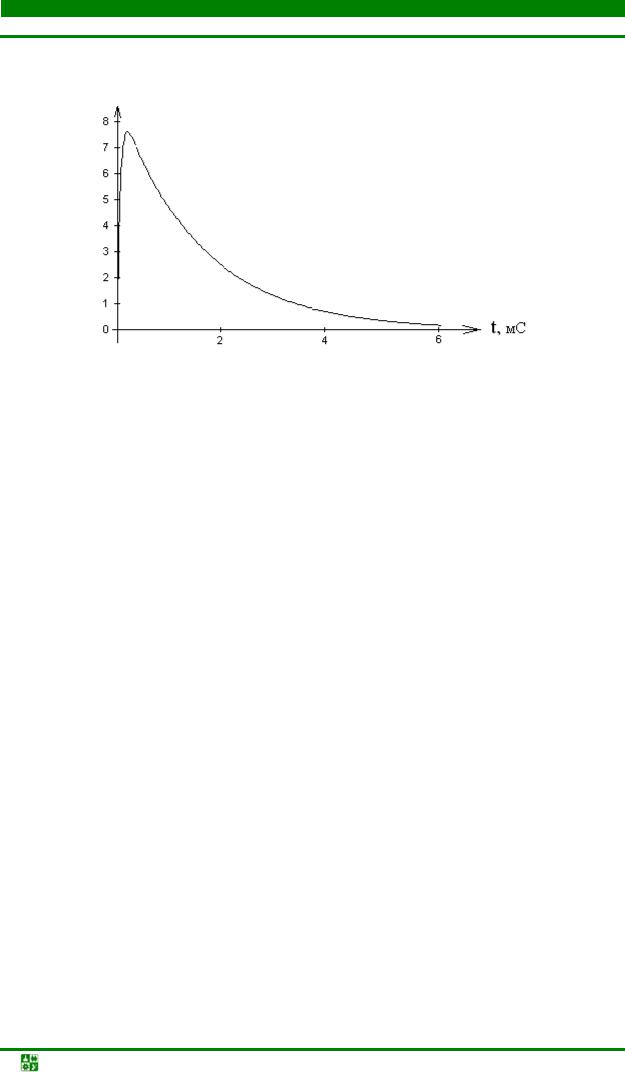
ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Связь интеграла Дюамеля с интегралом наложения

g(t), Сим/с

				t, мс
Рис. 23.9					Em
Отклик цепи на первом интервале 0 ≤ t ≤ τи		e	(τ)= kτ , где k =		Em	,
Отклик цепи на первом интервале 0 ≤ t ≤ τи		e	(τ)= kτ , где k =			,
	2	11			τи
	2				τи
t
i3 (t )= kt (A0 + A1 + A2 )+ ∫e11	(τ)g (t − τ)dτ =
0

= kt (A0 + A1 + A2 )+ ∫kτ p1A1ep1(t−τ) + p2 A2ep2(t−τ) dτ.

После несложных преобразований с учетом

A0 + A1 + A2 = h(0) = 0

получим выражение, совпадающее с выражением, приведенным в примере 5.

τи

p1 t−

t−

i3 (t )= Em

τи

A1ep1 t−

A2ep2 t−

A1ep1t

A2ep2t

−

−p τ

−p

−p τ

−p

1 и

На интервале времени от

τи

до τи

Основы теории цепей. Конспект лекций

-234-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Связь интеграла Дюамеля с интегралом наложения

τи

(t )=

(t−τ)

p A e

(t−τ)

dτ+

∫

τ p A e 1

2 2

h(0)

p A ep1(t−τ)

+ p A ep2

(t−τ) dτ.

∫

1 1

τи

Учитывая, что –A0 = A1 + A2, получим результат, совпадающий с решением в примере 5.

i3 (t )= Em A0 +2

		p	t−	τи
	A e	1
				2
+	1				+
	−p τ

			1 и

ep1 t− 2и

ep2 t

−

τи

A2ep2 t

−

A1ep1t

A2ep2t

−p

−

−p τ

Расчет отклика цепи при t > τи следует проводить с учетом всего входного сигнала

τи

(t )=

(t−τ)

∫

τ p A e 1

+ p A e

dτ+

τи

p1(t−τ)

p2(t−τ)

+ ∫

+ p2 A2e

Em p1A1e

dτ.

τи

(t )

= E

p1 t−

A1 ep1 t− 2и

ep2 t−

2и

A1e

−p τ

τи

A ep2 t

−

A ep1t

A ep2t

(t−τ

)

(t−τ

)

−

− A − A e

− A e

−p2τи

−p1τи

−p2τи

Полученные результаты полностью совпадают с откликом, рассчитанным с помощью интеграла Дюамеля.

Основы теории цепей. Конспект лекций

-235-

ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

Контрольныевопросы

1.Что представляет собой единичная функция?

2.Что называется переходной характеристикой цепи?

3.Какова размерность переходной характеристики цепи?

4.Какие ограничения накладываются на цепи при расчете переходных процессов с помощью интеграла Дюамеля?

5.Что представляет собой импульсная функция?

6.Что называется импульсной характеристикой цепи?

Основы теории цепей. Конспект лекций

-236-

ЛЕКЦИЯ 24. ОПЕРАТОРНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЦЕПЕЙ

Отклик на экспоненциальное воздействие. Понятие об операторных характеристиках. Определение операторных характеристик.

Откликнаэкспоненциальноевоздействие.

Во многих случаях воздействующая функция может быть представлена в обобщенной форме

e(t )= Eest ,

где E и s – комплексные числа: обобщенная (комплексная) амплитуда

E= Ee jψ , обобщенная (комплексная) частота s = σ + jω.

Взависимости от величин, определяющих экспоненциальное воздейст-

вие, получается тот или иной закон изменения e(t).

Если мнимая часть обобщенной частоты не равна нулю Jms ≠ 0 , то

e(t) = Eejψeσtejωt

и характер воздействующей функции зависит от вещественной части σ

(рис. 24.1):

а) при σ = 0	e(t )= Ee jψe jωt ;
б) при σ > 0	e(t )= Ee jψeσte jωt ;
в) при σ < 0	e(t )= Ee jψe−σte jωt ;
если Jms = ω= 0, то	e(t )= Ee jψeσt ;
г) при σ = 0	e(t )= Ee jψ ;
д) при σ > 0	e(t )= Ee jψeσt ;
е) при σ < 0	e(t )= Ee jψe−σt .

Таким образом, s = σ + jω имеет мнимую часть, которая может быть

рассмотрена как угловая частота некоторого гармонического колебания, а вещественная часть как коэффициент, характеризующий изменение огибающей этого колебания.

Вследствие того, что интегрирование и дифференцирование экспоненциальной функции не изменяет ее вида, отклик цепи на данное воздействие

Основы теории цепей. Конспект лекций

-237-

ЛЕКЦИЯ 24. ОПЕРАТОРНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЦЕПЕЙ

Отклик на экспоненциальное воздействие

является экспоненциальной функцией той же частоты, причем отношение отклика цепи к воздействию в этом случае не зависит от времени.

e(t)

	t		t
		0
0
0

	а		г

		e(t)
e(t)		e(t)
e(t)

			t
0			t

							t

				0
		б		0		д
		б				д

					e(t)
	e(t)				e(t)
	e(t)

Рис. 24.1

При e(t ) = Eest

IR =

Eest

, IC

= C

dUC

= sCEest , IL =

∫

ULdt =

Eest .

Входное сопротивление пассивного линейного двухполюсника

Z (s)=

e(t)

ZR (s)

= R, ZC (s)=

ZL (s)= sL.

I (t)

Основы теории цепей. Конспект лекций

-238-

ЛЕКЦИЯ 24. ОПЕРАТОРНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЦЕПЕЙ

Отклик на экспоненциальное воздействие

Полагая s = p, получим выражения для операторных сопротивлений идеализированных элементов цепи, полагая s = jω – выражения для комплексных входных сопротивлений элементов при гармоническом воздействии.

Следовательно, оператор преобразования Лапласа можно рассматривать как обобщенную (комплексную) частоту экспоненциального воздействия вида e(t )= Eest .

Понятиеобоператорныххарактеристиках.

Рассмотрим идеализированную линейную цепь, не содержащую независимых источников тока и напряжения (рис. 24.2).

i	Ii	Ik→k
	Ii
	Ui	Zk	Uk
г	Ui	Zk	Uk
i			k
		Рис. 24.2

Операторной, или обобщенной, частотной характеристикой Hki(p) линейной цепи называется отношение операторного изображения отклика цепи Y(p) к операторному изображению внешнего воздействия X(p) при нулевых начальных условиях:

(p)=

Yk (p)

(p)

=i y

(t ),

(p)

=i x

(t ).

Xi (p)

Операторная характеристика линейной цепи численно равна отношению отклика цепи к внешнему воздействию при внешнем воздействии вида

Для перехода от операторной характеристики цепи к ее комплексной частотной характеристике (КЧХ) необходимо заменить р на jω, т. е. КЧХ есть частный случай обобщенной частотной характеристики при р = jω.

Операторная характеристика цепи определяется только видом цепи и параметрами входящих в нее элементов.

Как и КЧХ, операторные характеристики делятся на входные и передаточные. В зависимости от того, какая величина выступает в качестве внешнего воздействия, а какая в качестве отклика, различают:

1. Операторное входное сопротивление

Основы теории цепей. Конспект лекций

-239-

ЛЕКЦИЯ 24. ОПЕРАТОРНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЦЕПЕЙ

Понятие об операторных характеристиках

Zii (p)= Ui((p));

Ii p

2. Операторную входную проводимость

Yii (p)= UIii((pp));

3. Операторный коэффициент передачи по напряжению

Kki (p)= UUki ((pp));

4. Операторный коэффициент передачи по току

KIki (p)= IIki ((pp));

5. Операторное передаточное сопротивление

Zki (p)= Uk((p));

Ii p

6. Операторную передаточную проводимость

Yki (p)= UIki ((pp));

Определениеоператорныххарактеристик.

Для расчета обобщенной характеристики цепи можно применить любые известные методы, например метод контурных токов, метод узловых напряжений, метод эквивалентного генератора и др.

Если сложная цепь содержит только один источник Ei(p), включенный в i-м контуре, то контурный ток, создаваемый при этом в другом k-м контуре

Ik (p)= Ei (p) ikZ ((pp)) ,

Основы теории цепей. Конспект лекций

-240-

ЛЕКЦИЯ 24. ОПЕРАТОРНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЦЕПЕЙ

Определение операторных характеристик

где Z(p) – определитель системы уравнений, составленных методом контур-

ных токов (в операторной форме); ik(p)	– алгебраическое дополнение эле-
мента в операторной форме
ik(p) = (–1)i + k	ikm(p).

Минор ikm(p) равен определителю системы, из которого исключена i-я строка, соответствующая i-му контуру, где действует ЭДС Ei(p), и k-й столбец, соответствующий искомому k-му току. Следовательно,

Uk (p)= Ik (p)Zk (p)=

Ei (p) ik (p)Zk (p)

и тогда

Z (p)

(p)=

Ei (p)

(p)

;

Y (p)=

(p)

;

(p)

Kki (p)=

Uk (p)

ik (p)Zk

(p)

; Zki

(p)=

Uk (p)

ik (p)Zk (p)

;

Ei (p)

Z (p)

(p)

ii (p)

(p)=

Ik (p)

ik (p)

; Y

(p)=

(p)

ik (p)

(p)

Iki

(p)

Поскольку

Z(p),

ii(p),

ik(p) представляют собой полиномы от собст-

венных и взаимных операторных сопротивлений независимых контуров цепи, а сопротивления являются рациональными функциями р с вещественными коэффициентами, любая операторная характеристика линейной цепи также является рациональной функцией р с вещественными коэффициентами, т. е. может быть представлена в виде отношения двух полиномов

Hki (p)=	N (p)	=	an pn + an−1 pn−1 +…+ a1 p + a0	.
	M (p)
			bm pm +bm−1 pm−1 +…+b1 p +b0

Решив уравнения N(p) = 0 и M(p) = 0 и разложив N(p) и M(p) на множители, получим

Hki (p)= K	(p − p01 )(p − p02 )…(p − p0n )	,
	(p − pX 1 )(p − pX 2 )…(p − pXm )

Основы теории цепей. Конспект лекций

-241-

ЛЕКЦИЯ 24. ОПЕРАТОРНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЦЕПЕЙ

Определение операторных характеристик

где K = an – масштабный коэффициент; p01, p02, ..., p0n – нули функции; pX1, bm

pX2, ..., pXm – полюсы функции Hki(p).

Таким образом, операторная характеристика может быть задана распределением нулей и полюсов (значений р, при которых функция обращается в бесконечность), а также масштабным коэффициентом K.

Операторные характеристики цепи удобно использовать при нахождении переходной и импульсной характеристик. Действительно, исходя из определения операторной характеристики, изображение отклика

Yk(p) = Hki(p)Xi(p).

С другой стороны, изображение отклика цепи на единичную функцию на входе является изображением переходной характеристики

Аналогично изображение отклика цепи на дельта-функцию является изображением импульсной характеристики

G (p)= Hki (p)Xi (p) Xi (p)=1, g (t )i=i G(p)= Hki (p),

Xi (p)=1i=i δ(t )

δ(t )			∞
	i		∫
		=i		δ(t )e− pt dt =1 .
			0

Пример 7. Для электрической цепи, приведенной в примере 1, определить переходную и импульсную характеристики, используя операторную характеристику.

Решение. Найдем операторную характеристику цепи (рис. 24.3).

I1(р)

I3(р)

I2(р)

рL

E1(р)

рС

Рис. 24.3

(p)=

I3 (p)

E1 (p)

Z (p)

(R1 + R3 + Z (p))(R2 + pL) E1 (p)

E1 (p)

Основы теории цепей. Конспект лекций

-242-

ЛЕКЦИЯ 24. ОПЕРАТОРНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЦЕПЕЙ

Определение операторных характеристик

где

Z (p)=	R	+ pL
	2		.
	1+(R + pL)pC
	2

Подставив значения R, L, C в последнее выражение, получим

Y31	(p)=			1		,
		60	10-7 p2	+1210 10-4	p +80

отсюда переходная характеристика

h(t )i=i Y31p(p)

и импульсная характеристика

g (t )i=i Y31 (p).

Контрольныевопросы

1.Что представляет собой экспоненциальное воздействие?

2.Что называется операторной, или обобщенной, частотной характеристикой линейной цепи?

3.Как определяются операторные характеристики цепи?

4.Как определить переходную и импульсную характеристики, используя операторную характеристику цепи?

Основы теории цепей. Конспект лекций

-243-

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 1516 / 3516 17 18 19 20 21 22 23 24 25 26 27 28 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.03.201616.34 Кб102ОТИ практическая 2.docx
#
06.03.201612.81 Кб34ОТИ практическая 3.docx
#
06.03.201697.04 Кб25ОТИ практическая 4.docx
#
06.03.20161.42 Mб35ОТИ практическая 5.docx
#
12.08.2019143.26 Кб1Отсканировано 14.02.2012 15-37.rtf
#
17.03.20156.1 Mб1071ОТЦ лекции.pdf
#
17.03.2015958.14 Кб18Отчёт Бондарев 5 работа.docx
#
17.03.201522.24 Кб105Отчет по практике.docx
#
17.03.201561.95 Кб159Отчет по практике_образец.doc
#
09.11.2019152.26 Кб3Отчет по производственной практике-3.rtf
#
17.03.201584.18 Кб85отчёт работа 6.docx