
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •ЛЕКЦИЯ 5. МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД
- •ЛЕКЦИЯ 7. МОЩНОСТЬ В ЦЕПИ ГАРМОНИЧЕСКОГО ТОКА
- •ЛЕКЦИЯ 8. ИЗБИРАТЕЛЬНЫЕ (РЕЗОНАНСНЫЕ) ЦЕПИ
- •ЛЕКЦИЯ 9. ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР
- •ЛЕКЦИЯ 10. СЛОЖНЫЕ СХЕМЫ ПАРАЛЛЕЛЬНЫХ КОНТУРОВ
- •ЛЕКЦИЯ 11. КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ. СВЯЗАННЫЕ КОНТУРЫ
- •ЛЕКЦИЯ 12. НАСТРОЙКА СВЯЗАННЫХ КОНТУРОВ
- •ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
- •ЛЕКЦИЯ 14. ОСНОВЫ ТЕОРИИ ЧЕТЫРЕХПОЛЮСНИКОВ
- •ЛЕКЦИЯ 15. ХАРАКТЕРИСТИЧЕСКИЕ (ВТОРИЧНЫЕ) ПАРАМЕТРЫ ЧЕТЫРЕХПОЛЮСНИКА
- •ЛЕКЦИЯ 17. СЛОЖНЫЕ ЧЕТЫРЕХПОЛЮСНИКИ
- •ЛЕКЦИЯ 18. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- •ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
- •ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ
- •ЛЕКЦИЯ 25. ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
- •ЛЕКЦИЯ 26. ФИЛЬТРЫ ВЕРХНИХ ЧАСТОТ
- •ЛЕКЦИЯ 27. ПОЛОСОВЫЕ ФИЛЬТРЫ
- •ЛЕКЦИЯ 28. ФИЛЬТРЫ ТИПА M
- •ЛЕКЦИЯ 29. БЕЗЫНДУКЦИОННЫЕ ФИЛЬТРЫ
- •ЛЕКЦИЯ 30. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- •ЛЕКЦИЯ 31. РЕЖИМ БЕГУЩИХ ВОЛН
- •ЛЕКЦИЯ 32. РЕЖИМ СТОЯЧИХ ВОЛН
- •ЛЕКЦИЯ 33. РЕЖИМ СМЕШАННЫХ ВОЛН
- •ЛЕКЦИЯ 34. СОГЛАСОВАНИЕ ЛИНИИ С НАГРУЗКОЙ
- •ЛЕКЦИЯ 35. ЧЕТВЕРТЬВОЛНОВЫЙ ТРАНСФОРМАТОР
- •ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ
- •ЛЕКЦИЯ 37. СИНТЕЗ ДВУХПОЛЮСНИКОВ
- •ЛЕКЦИЯ 38. СВОЙСТВА И РЕАЛИЗАЦИЯ ВХОДНЫХ ФУНКЦИЙ RC-ДВУХПОЛЮСНИКОВ
- •ЛЕКЦИЯ 39. СИНТЕЗ RLC-ДВУХПОЛЮСНИКОВ
- •ЛЕКЦИЯ 40. СИНТЕЗ ЧЕТЫРЕХПОЛЮСНИКОВ
- •ЛЕКЦИЯ 41. ЛЕСТНИЧНЫЕ ЦЕПИ С ЭЛЕМЕНТАМИ ДВУХ ТИПОВ
- •ЛЕКЦИЯ 42. РЕАЛИЗАЦИЯ ЧЕТЫРЕХПОЛЮСНИКОВ МЕТОДОМ ДАРЛИНГТОНА
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
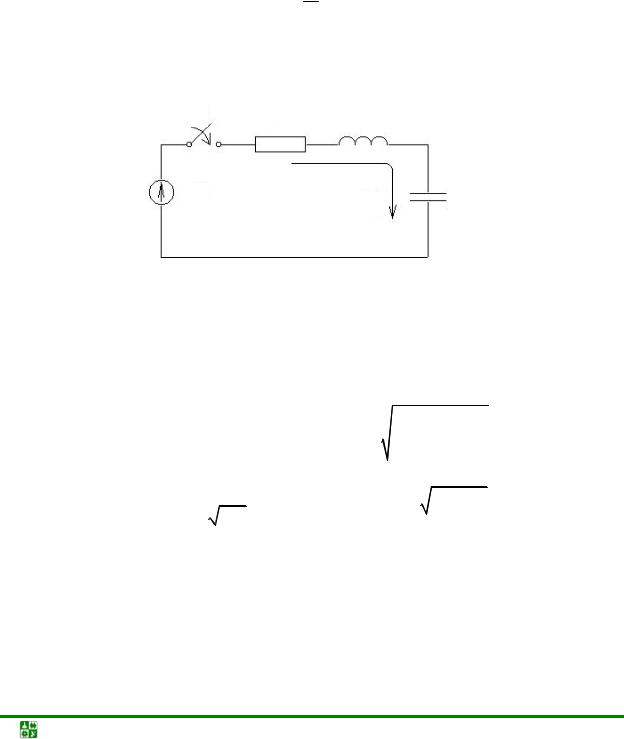
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в RLC-цепь постоянного напряжения. Включение в цепь RLC гармонического напряжения.
Если RLC-цепь (рис. 20.1), не имеющая начального запаса энергии электрического и магнитного полей, подключается к источнику внешнего напряжения в момент времени t = 0, то для t ≥ 0 справедливо уравнение
Ri + L dtdi + C1 ∫idt = e(t ),
имеющее решение для тока i(t) = iПР(t) + iCB(t).
t = 0
R L
e(t) |
i(t) |
C |
|
Рис. 20.1
Свободная составляющая i |
|
|
(t )= A e p1t + A ep2t , |
|
|
|
|
|
|
|||||||
|
|
|
|
СВ |
1 |
2 |
|
|
|
|
|
|
|
|||
где p1 и р2 – корни характеристического уравнения |
|
|
|
|
||||||||||||
|
Lp2 + Rp + |
1 |
= 0, p = − |
R |
± |
R |
2 |
− |
1 |
, |
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
C |
1,2 |
2L |
|
LC |
|||||||
|
|
|
|
|
|
|
2L |
|
||||||||
Обозначив δ = |
R |
, |
ω = |
|
1 |
|
, получим |
p = −δ ± |
δ2 −ω2 . |
|||||||
|
|
|
|
|
||||||||||||
|
2L |
0 |
|
LC |
1,2 |
|
|
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
А1 и А2 – постоянные интегрирования, определяемые начальными условиями в цепи; iПР(t) – принужденная составляющая тока, определяемая видом ЭДС e(t) и величинами R, L, C.
Основы теории цепей. Конспект лекций |
-172- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
ВключениевRLC-цепьпостоянногонапряжения.
При подключении источника постоянного напряжения iПР(t) = 0, так как постоянный ток через конденсатор не течет:
i(t )= i |
(t )= A ep1t + A ep2t , |
di = p A ep1t + p |
2 |
A ep2t . |
|||
СВ |
1 |
2 |
dt |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
Для t = 0 e(0)= Ri(0)+ L di |
(0) |
+UC (0), |
di (0)= |
E |
||||||||||
L |
||||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
dt |
||
(так как iL(0) = iL(0–) = 0, |
UC(0) = UC(0–) = 0). |
|
||||||||||||
|
|
A1 + A2 = 0, |
|
|
|
|
|
|||||||
Таким образом, |
|
|
|
|
|
|
|
|
E |
|
|
|
||
|
p A + p A = |
|
, |
|
|
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||
|
1 1 |
2 |
|
2 |
|
L |
|
|
|
|||||
|
|
|
E |
|
|
|
|
|
|
|
|
|||
откуда A1 = −A2 = |
|
|
|
|
, |
|
|
|
|
|
|
|||
L(p − p |
|
) |
|
|
|
|
|
|
||||||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|||
следовательно, |
i(t )= |
E |
|
|
(ep1t −ep2t ). |
|
||||||||
L(p − p |
|
) |
|
|||||||||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|||
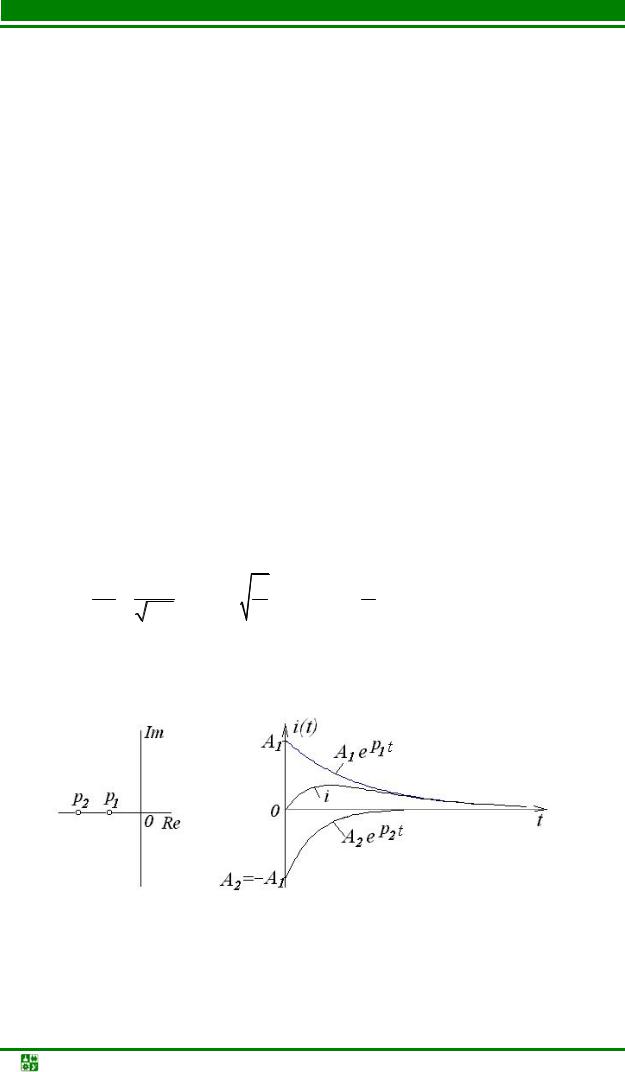
В зависимости от соотношения δ и ω0 (ω0 – резонансная частота) возможны три случая:
а) δ > ω0 , 2RL > LC1 , R > 2 CL = 2ρ, Q = Rρ < 0,5 (апериодический процесс).
В плоскости комплексного переменного корни характеристического уравнения лежат на вещественной оси (рис. 20.2). Ток в цепи представляет собой сумму двух экспонент (рис. 20.3).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
A ep1t |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|||||||
p2 |
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
t |
||||||
|
|
|
|
|
|
Re |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A ep2t |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 = –A1 |
|
|
|
|
|
|
|
|
|
||||
Рис. 20.2 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 20.3 |
|
|||||||||
Основы теории цепей. Конспект лекций |
-173- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в RLC-цепь постоянного напряжения
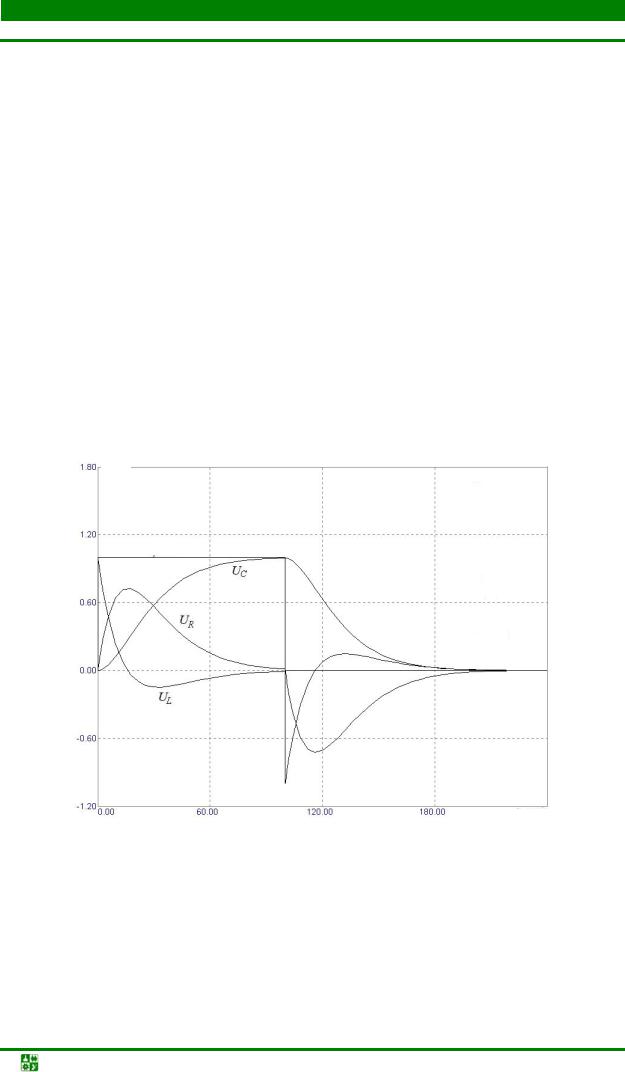
Напряжения на элементах: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UR = Ri(t )= |
ER |
|
|
(e p1t −ep2t ), |
|
|
|
||||||||
L(p − p |
2 |
) |
|
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
di |
|
E |
|
|
|
(p1e |
p t |
p t |
), |
|
|
||||
UL = L dt = |
|
|
|
1 |
− p2e |
2 |
|
|
|||||||
(p − p |
2 |
) |
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
p t |
|
|
p t |
|
|
UC = E −UR −UL = E 1+ |
|
|
(p2e 1 |
− p1e |
2 |
) . |
|||||||||
(p |
− p ) |
||||||||||||||
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
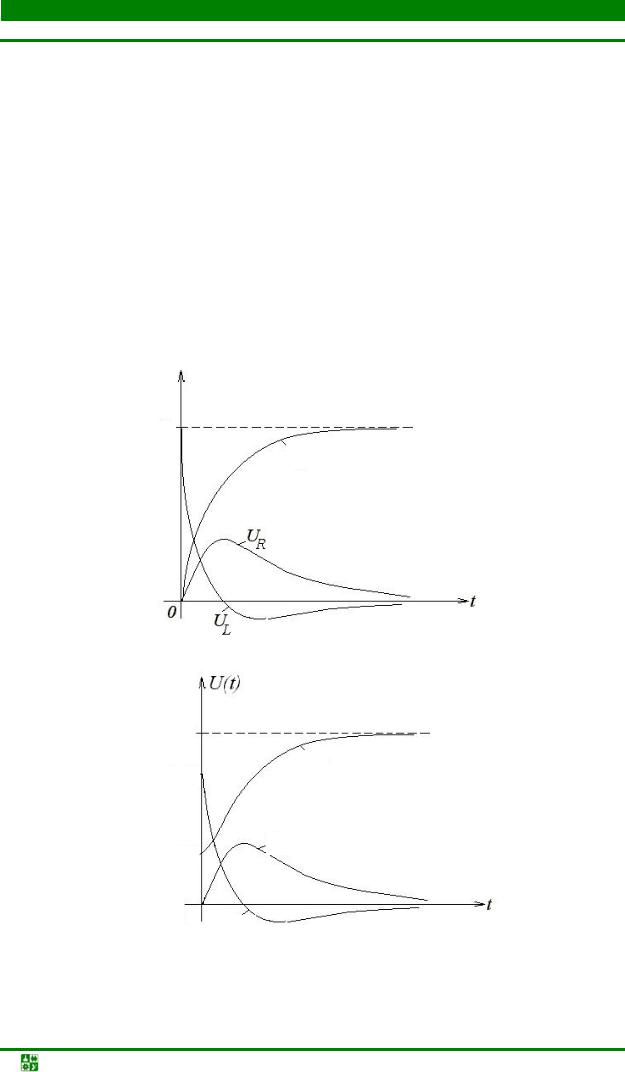
Графики зависимостей UR, UL, UC от времени приведены на рис. 20.4.
U(t)
E
UC
|
|
|
|
|
UR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
0 |
|
|
|
|
|
||
|
UL |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рис. 20.4 |
||
|
|
|
|
|
|
||
|
|
|
|
||||
|
|
U(t) |
|||||
|
|
|
|
|
|
|
|
E
UC
E – U
UR
U
0 UL
Рис. 20.5
Основы теории цепей. Конспект лекций |
-174- |

ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в RLC-цепь постоянного напряжения
Если в момент коммутации емкость была заряжена до напряжения U, то для t = 0
|
|
|
|
|
E = L di |
+U , |
|
||
|
|
|
|
|
|
|
dt |
|
|
откуда di (0)= E −U и |
A = −A = |
|
E −U |
, |
|||||
|
|
||||||||
dt |
L |
|
1 |
2 |
|
L( p1 − p2 ) |
|
||
E −U |
|
|
|
|
|||||
|
|
|
p t |
|
p t |
|
|||
следовательно, i(t )= |
|
|
|
(e 1 |
−e |
2 ). |
|
||
L(p |
− p |
) |
|
||||||
|
|
1 |
2 |
|
|
|
|
|
|
Кривые зависимостей напряжений на элементах цепи при ненулевых начальных условиях показаны на рис. 20.5.
б) δ = ω0, R = 2ρ, Q = 0,5 (критический режим).
p1,2 = –δ, в этом случае выражение для тока приводит к неопределенности вида 0/0, раскрывая которую по правилу Лопиталя, получим
i(t )= lim |
E |
|
|
|
|
|
|
e p1t −ep2t |
|
= |
E |
te−δt , |
||||
L(p − p |
)( |
) |
|
|||||||||||||
p1→p2 |
|
|
|
|
L |
|||||||||||
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
при ненулевых начальных условиях |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i(t )= lim |
|
E −U |
|
|
|
|
ep1t −ep2t |
|
= |
|
E −U |
te−δt |
||||
|
|
|
)( |
) |
|
|||||||||||
p1→p2 L(p − p |
2 |
|
|
|
|
|
|
L |
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(действительно, дифференцированием числителя и знаменателя по p1 полу-
|
′ |
|
|
|
− p1t |
|
|
|
|
чаем i(t )= lim |
ϕ (p1 ) |
= |
lim |
Ete |
= |
E |
te−δt ). |
||
|
|||||||||
|
L |
L |
|||||||
p1→p2 =−δ ψ′(p1 ) |
|
p1→ −δ |
|
|
|||||
Форма кривых зависимостей тока и напряжений на R, L, C от времени аналогична апериодическому режиму, условие Q = 0,5 является предельным условием существования в цепи апериодических процессов.
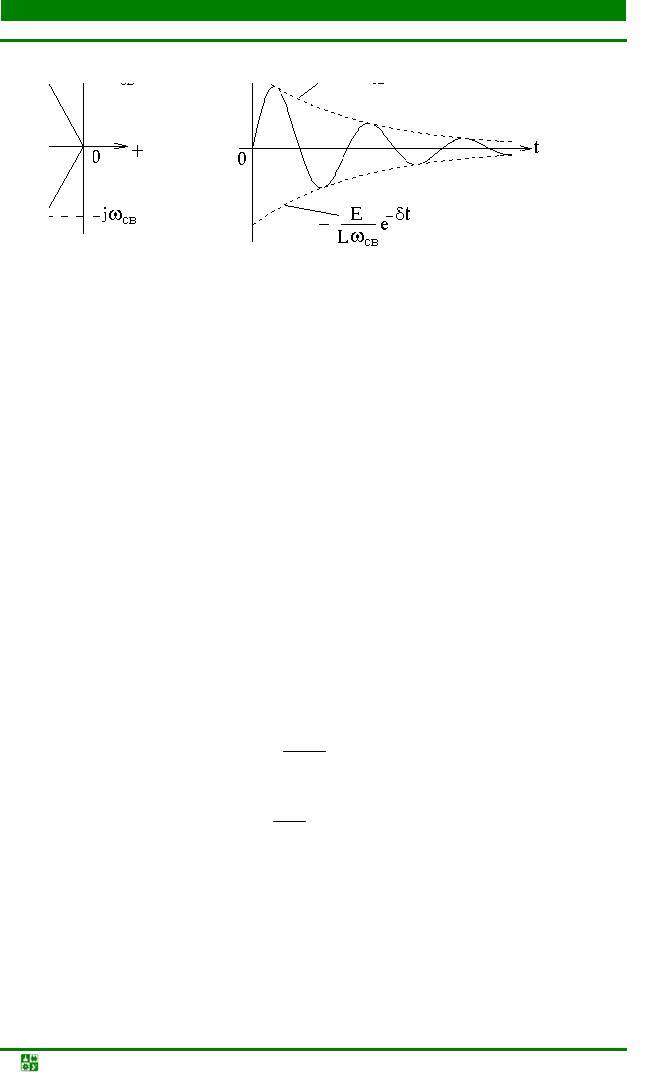
в) δ < ω0, R < 2ρ, Q > 0,5, p1,2 = –δ ± jωCB (колебательный процесс).
Корни характеристического уравнения комплексно-сопряженные (рис. 20.6). ωСВ = ω02 −δ2 – угловая частота свободных (собственных) колебаний.
Основы теории цепей. Конспект лекций |
-175- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в RLC-цепь постоянного напряжения
|
|
|
|
|
|
|
|
+j |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
е−δt |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
р1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
jωСВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LωСВ |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–jωСВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|||||||||
|
|
р2 |
|
|
|
|
|
|
|
|
|
|
− |
е |
−δt |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LωСВ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Рис. 20.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 20.7 |
|
|
|
|
|
|
|
||||||||||||||
При p1,2 = –δ ± jωCB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i(t )= |
E |
|
|
(e(−δ+ jωСВ)t |
−e(−δ− jωСВ)t )= |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 jω |
|
L |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
E |
|
|
|
e−δt (cosω |
|
t + j sin ω |
t |
−cosω |
|
t |
+ j sin ω |
t )= |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
2 jωСВL |
|
|
|
|
|
СВ |
|
|
|
СВ |
|
|
|
|
|
|
СВ |
|
|
СВ |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
E |
e−δt sin ω |
|
t. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωСВL |
|
|
|
|
СВ |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
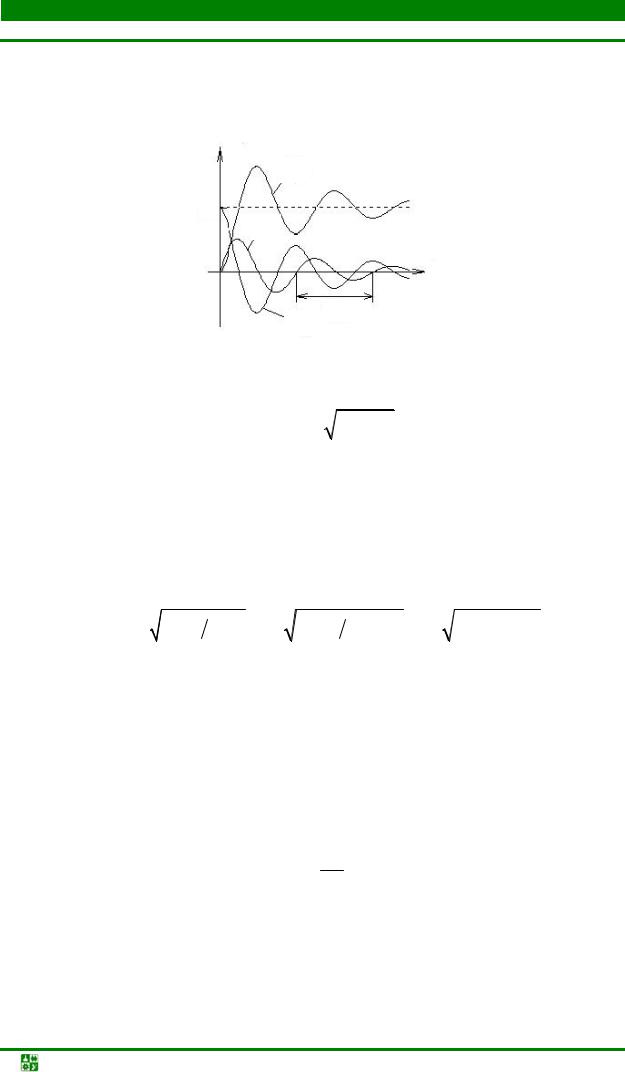
Таким образом, ток в цепи представляет собой затухающую гармоническую функцию, амплитуда которой экспоненциально уменьшается во вре-
мени (рис. 20.7).
Напряжение на элементах цепи:
UR = Ri = ωERL e−δt sin ωСВt,
СВ
UL = L di = − ω0 Ee−δt sin (ωСВt −ϕ), dt ωСВ
|
U |
C |
= E −U |
R |
−U |
L |
= E |
1− |
ω0 |
e−δt sin (ω |
t + ϕ) |
, |
|
|
ω |
||||||||||||
|
|
|
|
|
|
|
СВ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
СВ |
|
|
|
где ϕ = arctg |
ωСВ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
δ |
|
|
|
|
|
|
|
|
|
|
|
|
Основы теории цепей. Конспект лекций |
-176- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в RLC-цепь постоянного напряжения
Графики зависимостей UR, UL, UC от времени приведены на рис. 20.8.
U
UC
E
UR
t
0
ТСВ
UL
Рис. 20.8
T |
= |
2π |
= |
2π |
. |
|
|
ω2 |
−δ2 |
||||
CB |
|
ωCB |
|
|||
|
|
|
|
0 |
|
|
Очевидно, что чем меньше δ, тем медленнее затухают колебания в цепи.
Скорость затухания колебаний оценивают величиной e δTСВ – декрементом затухания, где TCB – период свободных колебаний, а также логарифмиче-
ским декрементом затухания |
ne δTСВ = δT . |
|
|
|
||
Учитывая, что |
|
СВ |
|
|
|
|
|
|
|
|
|
||
ω = ω 1−(δ ω )2 |
= ω 1−(R 2Lω )2 |
= ω 1−(1/ 2Q)2 |
, |
|||
СВ |
0 |
0 |
0 |
0 |
0 |
|
при высокой добротности ωCB ≈ ω0 и TCB ≈ T0 логарифмический декремент затухания
δТ |
|
= |
R |
T = |
Rω0 |
T = |
2πTСВ |
≈ |
π |
. |
|
|
|
|
|
||||||
|
СВ |
|
2L СВ |
2 ω L СВ |
2QT |
Q |
||||
|
|
|
|
|
0 |
|
|
|
|
|
Время практического существования переходного процесса определяется временем затухания экспоненты e–δt, которое составляет
(4 −5)1δ = (4 −5)2RL = (4 −5)τK ,
где τK – постоянная времени контура. За время переходного процесса tПР укладывается N периодов свободной составляющей, причем
Основы теории цепей. Конспект лекций |
-177- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в RLC-цепь постоянного напряжения
N = |
tПР |
= |
(4 −5)2 Lω0 |
= |
(4 −5)2QωСВ ≈ Q. |
||
|
T |
Rω |
|||||
|
Т |
СВ |
|
|
2πω |
||
|
|
|
СВ |
0 |
|
0 |
|
Таким образом, колебания затухают тем быстрее, чем меньше добротность контура.
Рассмотрим отклик цепи на прямоугольный импульс на входе. Представив прямоугольный импульс в виде разности двух одинаковых скачков напряжений, смещенных во времени на величину длительности импульса, найдем напряжение на элементах R, L, C как алгебраическую сумму откликов на каждый из скачков в отдельности.
Зависимости напряжений на элементах от времени в этом случае приведены для апериодического процесса (R = 300 Ом, L = 25 мГн, C = 10 нФ) на рис. 20.9, для колебательного процесса (R = 300 Ом, L = 70 мГн, C = 40 нФ)
на рис. 20.10.
U, В
UВХ
τи
t, мкс
Рис. 20.9
Основы теории цепей. Конспект лекций |
-178- |

ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в RLC-цепь постоянного напряжения
U, В
UВХ
τи
t, мс
Рис. 20.10
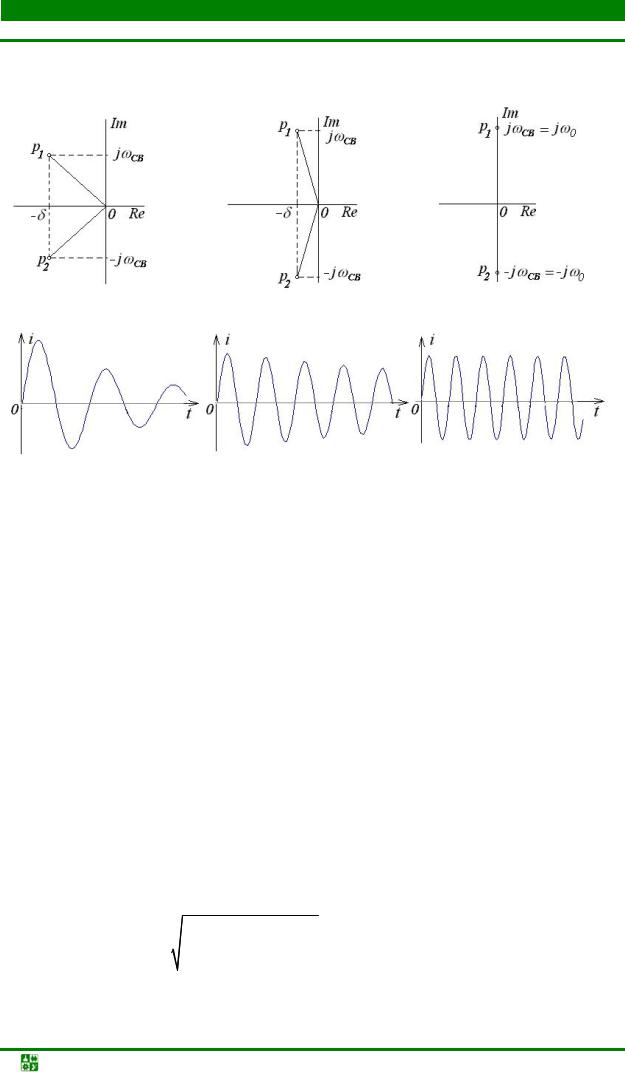
В общем же случае форма тока в цепи определяется расположением корней характеристического уравнения на комплексной плоскости
(рис. 20.11).
Im |
|
Im |
|
Im |
|
|
|
|
|
|
|
|
|
0 |
|
Re |
|
p2 |
|
|
|
0 |
|
Re |
|
p2 = p1 = –δ |
|
0 |
|
Re |
|
p2 |
|
p1 |
|
|
p1 |
|
|||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|||
|
|
i
0 |
|
t |
|
0 |
|
t |
|
0 |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Апериодический режим |
|
|
|
Критический режим |
||||||
|
R >> 2ρ |
|
R > 2ρ |
|
|
|
|
R = 2ρ |
|||
|
|
|
|
|
Рис. 20.11 |
|
|
|
|
|
|
Основы теории цепей. Конспект лекций |
-179- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в RLC-цепь постоянного напряжения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jωСВ = jω0 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
jωСВ |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
jωСВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
Re |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
Re |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–jωСВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–jωСВ |
|
|
|
|
|
|
|
|
|
|
|
–jωСВ = –jω0 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R < 2ρ |
|
|
|
|
|
|
Колебательный режим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R << 2ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R → 0 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 20.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
На рис. 20.12 показано изменение переходного процесса при изменении |
|||||||||||||||||||||||||||||||||||||||||||||
сопротивления потерь в контуре (индуктивность и емкость не меняются). Очевидно, что чем меньше сопротивление R, тем выше частота свободных колебаний в контуре и в пределе при стремлении R к нулю частота свободных колебаний стремится к резонансной частоте контура.
ВключениевцепьRLC гармоническогонапряжения.
Рассмотрим переходные процессы, возникающие в контуре при включении источника гармонического напряжения.
Пусть при t ≥ 0 внешняя ЭДС имеет вид e(t) = Emcos(ωt + ψ), тогда принужденный ток
i |
(t )= I |
m |
cos(ωt |
+ ψ −ϕ), |
где I |
m |
= |
|
Em |
|
, |
|
|
|||||||||
|
|
|
|
|||||||||||||||||||
|
ПР |
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
ωL − |
1 |
|
|
||||||
|
Z |
|
|
R |
2 |
|
ωL − |
|
|
ωC |
||||||||||||
|
|
|
|
, |
ϕ = arctg |
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
= |
|
+ |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
R |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Основы теории цепей. Конспект лекций |
-180- |

ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в цепь RLC гармонического напряжения
Полное решение для тока |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
i(t ) = I |
m |
cos(ωt + ψ −ϕ) |
+ A ep1t + A ep2t . |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
||||
При нулевых начальных условиях iL(0–) = 0, UC(0–) = 0 для |
t = 0 |
|
||||||||||||||||||||
имеемi(0–) = iL(0–) = 0 = iПР(0) + iCB(0). |
|
|
|
|
|
|
|
|
|
|||||||||||||
I |
m |
cos(ψ −ϕ)+ A |
|
+ A = 0, |
di (0)= |
e(0) |
= |
Em |
cosψ, |
|
||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
dt |
|
|
|
L |
|
L |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
di (0)= |
diПР |
(0)+ |
diСВ |
(0)= −ωI |
m |
sin (ψ −ϕ)+ p A |
+ p A |
, |
||||||||||||||
|
|
|||||||||||||||||||||
dt |
|
|
|
dt |
|
|
dt |
|
|
|
|
1 1 |
2 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
I |
m |
cos(ψ −ϕ)+ A |
+ A = |
0, |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||||
−ωI |
m |
sin (ψ −ϕ) |
+ p A + p A = |
Em |
cosψ. |
|
|
|||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 1 |
2 2 |
|
L |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда
A1
A2
= |
|
|
ω |
Im sin (ψ −ϕ)+ |
|
|
p2 |
Im cos(ψ −ϕ)+ |
|
Em |
|
cosψ, |
||||
p1 |
− p2 |
p1 |
− p2 |
L(p1 − p2 ) |
||||||||||||
|
|
|
|
|
|
|
||||||||||
= − |
|
ω |
|
Im sin (ψ −ϕ)− |
|
p1 |
|
Im cos(ψ −ϕ)− |
Em |
|
cosψ. |
|||||
|
|
|
|
|
|
L(p1 |
− p2 ) |
|||||||||
|
|
|
p1 − p2 |
|
|
p1 − p2 |
|
|
||||||||
Подставив постоянные интегрирования A1 и A2 в выражение для полного тока, получим
i(t )= Im cos(ωt |
+ ψ −ϕ)+ |
|
Im |
|
cos(ψ −ϕ)(p2ep1t − p1ep2t )+ |
||||||||
p1 − p2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
+ |
E |
|
|
ωL |
|
|
(e |
p t |
−e |
p t |
). |
||
L(p − p |
) cosψ + |
|
Z sin |
(ψ −ϕ) |
1 |
2 |
|||||||
|
m |
|
|
|
|
|
|
|
|
|
|
||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
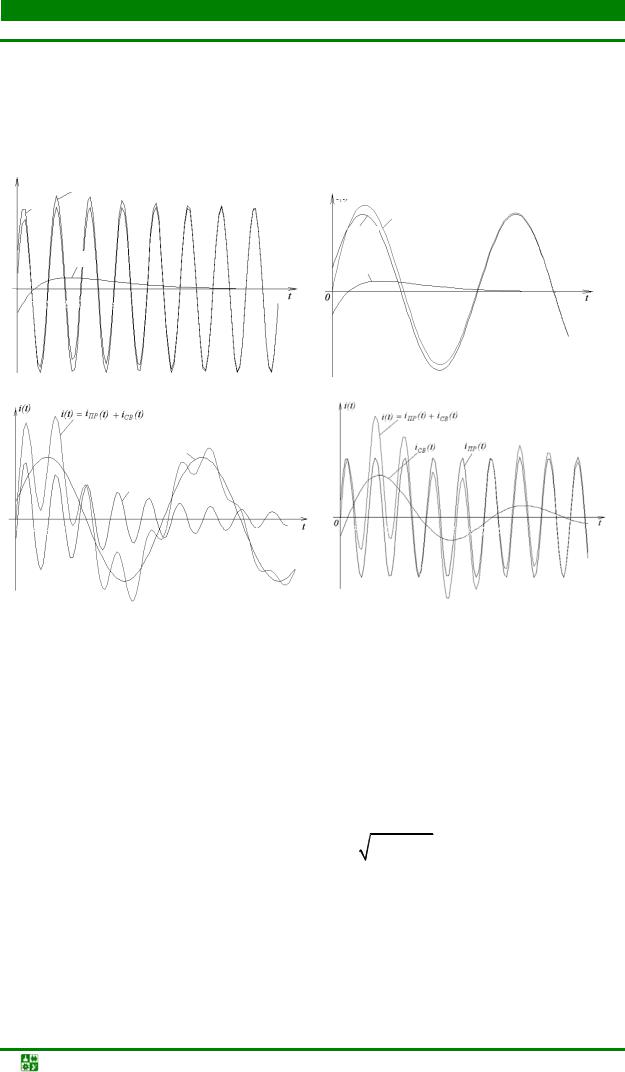
Кривые зависимости тока от времени представляют собой сумму кривых iПР и iCB. В зависимости от вида свободных составляющих (расположения корней характеристического уравнения на комплексной плоскости) и частоты внешней ЭДС возможны различные случаи. На рис. 20.13, а, б приведены формы тока в цепи при R > 2ρ (апериодический процесс), когда период принужденного тока меньше (рис. 20.13, а) и (рис. 20.13, б) больше длительности свободной составляющей тока.
Основы теории цепей. Конспект лекций |
-181- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в цепь RLC гармонического напряжения
При R < 2ρ форма переходного тока зависит от соотношения частоты внешней ЭДС и частоты свободных колебаний (на рис. 20.13, в приведена форма тока для ω < ωCB, на рис. 20.13, г – для ω > ωCB).
i(t) i(t) = iПР(t) + iСВ(t)
iПР(t)
iСВ(t)
0
i(t)
i(t) = iПР(t) + iСВ(t)
iПР(t)
iСВ(t)
t |
|
0 |
|
t |
а |
б |
i(t) |
|
i(t) = iПР(t) + iСВ(t) |
|
iПР(t)
iСВ(t)
0
i(t) |
|
|
|
|
|
|
i(t) = iПР(t) + iСВ(t) |
|
|||||
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
iПР(t) |
|
|
|
|
iСВ(t) |
|||
|
|
0 |
|
|
|
t |
|||||
t |
|||||
|
|
в |
г |
Рис. 20.13
Чаще всего на практике применяют колебательные контуры с малыми потерями (R << ρ). В этом случае
|
p |
− p |
2 |
= 2 jω |
и ep1t −ep2t = 2 je−δt sin ω t, |
|
|||||
|
1 |
|
|
СВ |
|
|
|
|
CB |
|
|
p ep1t − p ep2t |
= (−δ − jω |
|
)e(−δ+ jωСВ)t |
−(−δ + jω |
|
)e(−δ− jωСВ)t = |
|||||
2 |
1 |
|
|
|
СВ |
|
СВ |
|
|
||
= 2 j (δsin ω |
t + ω |
cosω |
t )e−δt = −2 j |
ω2 + δ2 |
(cosω |
t sin ϕ + |
|||||
|
СВ |
|
СВ |
СВ |
|
СВ |
|
СВ |
C |
||
+sin ωСВt cosϕC )e−δt = −2 jωСВe−δt sin (ωСВt + ϕC ),
ϕC = arctg ωδСВ .
Основы теории цепей. Конспект лекций |
-182- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в цепь RLC гармонического напряжения
Следовательно,
i(t )= Im cos(ωt + ψ −ϕ)− Im ω0 cos(ψ −ϕ)e−δt sin (ωСВt + ϕC )+
ωСВ
+ ωEmL cosψ + ωZL sin (ψ −ϕ) e−δt sin ωСВt.
СВ
Таким образом, характер переходных процессов в контуре определяется соотношением между резонансной частотой контура, частотой колебаний внешней ЭДС, а также частотой свободных колебаний.
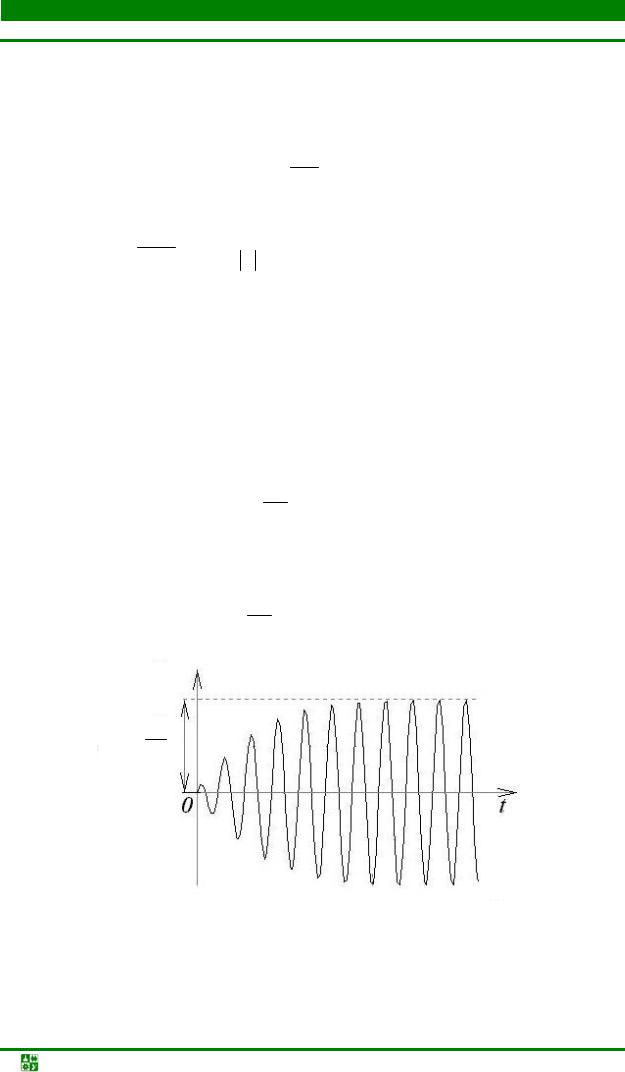
Чаще всего колебательный контур с малыми потерями (δ << ω0) работает на резонансной частоте, совпадающей с частотой внешней ЭДС. Если ψ = π/2, т. е. напряжение источника ЭДС в момент включения проходит через нуль, то ωCB ≈ ω0 ≈ ω, |Z| = R, φ = 0, φC = π/2,
i(t )≈ ERm (1−e−δt )sin ω0t.
Из последнего выражения следует, что амплитуда колебаний в контуре с течением времени растет по экспоненциальному закону, приближаясь к
принужденной составляющей ERm (рис. 20.14).
i
Im = ERm
0 |
|
t |
|
|
|
Рис. 20.14
Основы теории цепей. Конспект лекций |
-183- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в цепь RLC гармонического напряжения
Скорость нарастания амплитуды тока определяется производной
dtdi ,
где I (t ) = Im (1−e−δt ).
di (0) |
|
= Imδ, δ = |
|
R |
= |
|
Rω0 |
|
= |
|
ω0 |
= |
ΔωK |
, |
|||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
dt |
|
t=0 |
|
|
2L |
|
|
2ω0L |
2Q |
|
2 |
|
|||||
|
|
|
|
|
|
||||||||||||
|
|
di (0) |
|
|
ΔωK |
|
Im = |
Im |
. |
|
|
|
|||||
|
|
|
= |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
dt |
|
t=0 |
2 |
|
|
|
τK |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
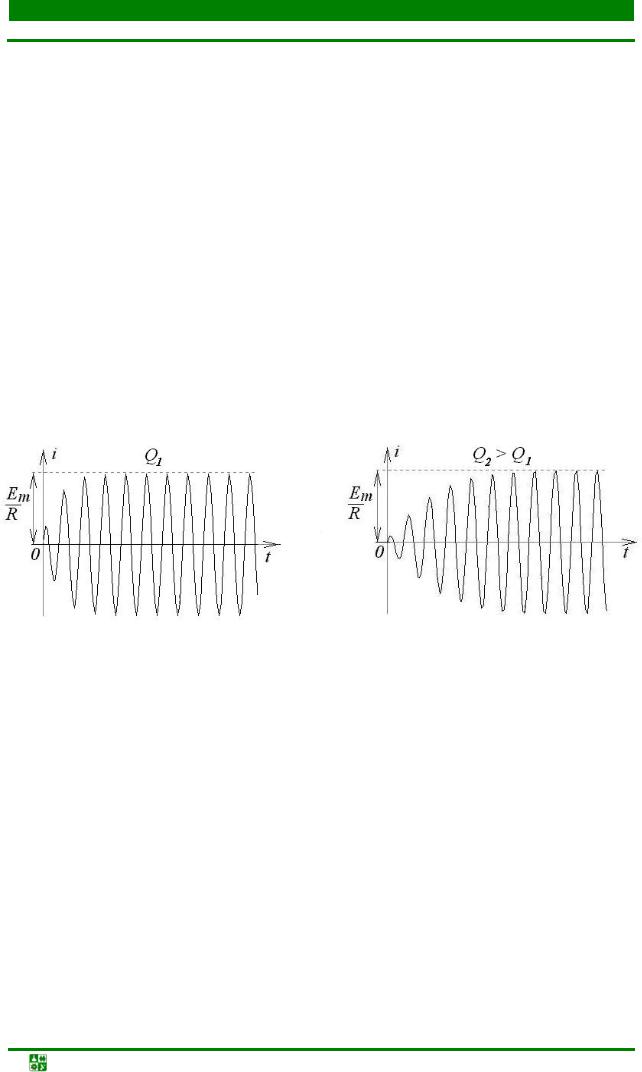
Таким образом, скорость нарастания тока тем больше, чем шире полоса пропускания контура, меньше добротность (рис. 20.15).
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
i |
|
Q2 > Q1 |
|
|
|
|
|
|
|
|
|
Q1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Em |
|
|
|
|
||||||
|
E |
|
|
|
|
|
|
|
|
|||||||||||||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
||||||||||
|
|
|
|
|
|
|
|
t |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
Рис. 20.15
Если же частота внешней ЭДС не совпадает с резонансной частотой контура, то при малых расстройках (ω0 ≈ ω)
i(t) = –Imsin(ωt – φ) + Ime–δt sin(ω0t – φ).
Если потери в контуре отсутствуют (δ = 0), то
i(t ) ≈ −Im sin (ωt −ϕ)+ Im sin (ω0t −ϕ) =
= −2I |
m |
sin |
ω−ω0 |
t |
sin |
ω+ ω0 t −ϕ |
|
; |
ω> ω , |
||
|
|
|
2 |
|
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
Основы теории цепей. Конспект лекций |
-184- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в цепь RLC гармонического напряжения
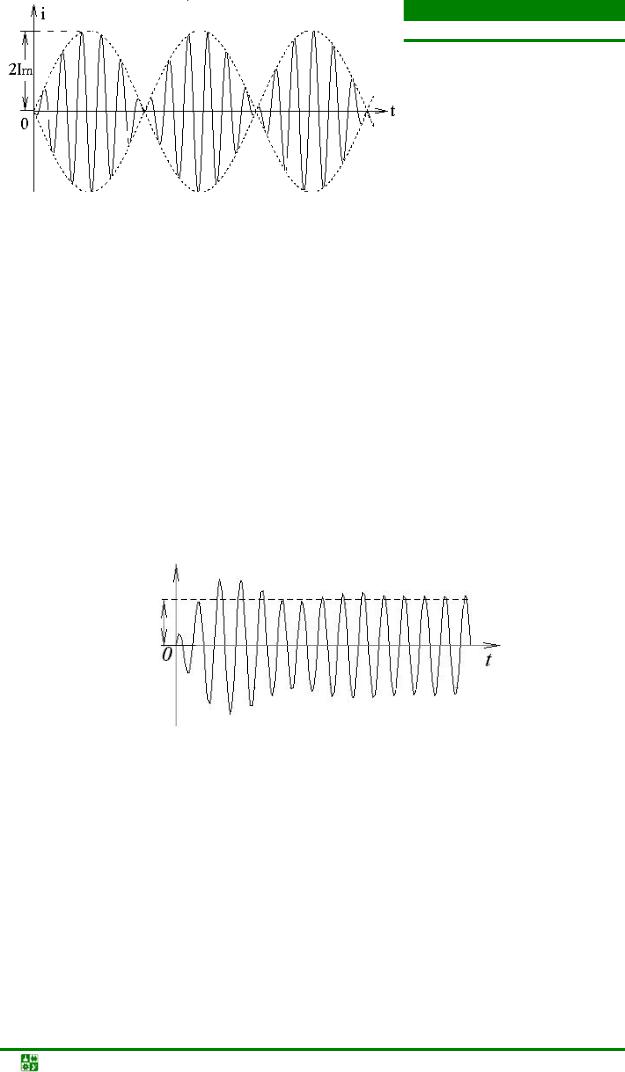
т. е. в результате сложения двух гармонических колебаний с близкими частотами в контуре возникают колебания с частотой ω+2ω0 ≈ ω и медленно из-
меняющейся амплитудой sin ω−ω0 t , так называемые биения (рис. 20.16).
2
Очевидно, что период огибающей тем больше, чем ближе частоты внешней ЭДС и резонанса контура.
В реальном контуре наличие потерь приводит к затуханию свободной составляющей тока, поэтому огибающая переходного процесса с течением времени будет стремиться к установившемуся значению Im (рис. 20.17).
i
2Im
t
0
Рис. 20.16
i
Im
0 |
|
|
|
t |
|||
|
|
Рис. 20.17
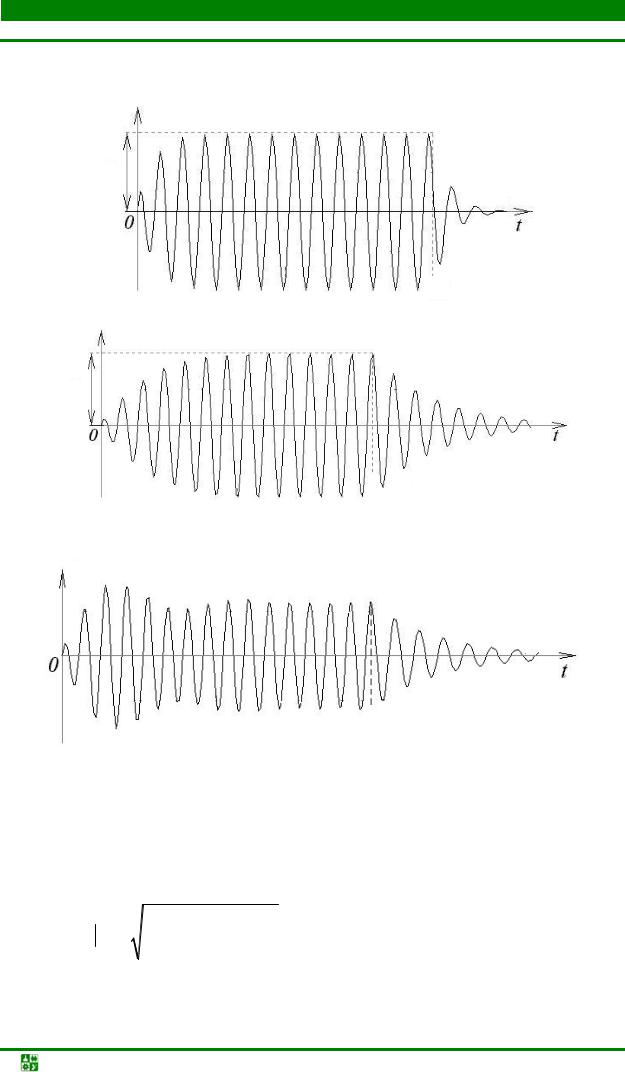
Отклик контура на радиоимпульс с прямоугольной огибающей в интервале времени от 0 до τи можно найти как отклик на гармоническую ЭДС, включенную в момент t = 0. Начиная с момента t = τи после прекращения действия внешней ЭДС остается только свободная составляющая тока
IСВ(t) = Im1e–δtsin(ωСВt – φ),
где Im1 определяется значениями напряжения на конденсаторе и тока в контуре в момент времени t = τи. Таким образом, полный отклик колебательного контура на радиоимпульс на входе имеет вид, представленный на рис. 20.18, а, для случая ω = ω0 и на рис. 20.18, б – для случая ω > ω0.
Основы теории цепей. Конспект лекций |
-185- |
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в цепь RLC гармонического напряжения
i
Im
0 |
|
|
|
t |
|
|
|
|
Q1 < Q2
τи
а
i
Im
0 |
|
t |
|
|
|
Q2 > Q1
τи
б
Рис. 20.18
i
0 |
|
|
|
t |
|||
|
|
τи
Рис. 20.19
Если частота внешней ЭДС значительно отличается от резонансной частоты контура с малыми потерями, то характер переходных процессов отличается от рассмотренных выше.
Предположим, что ω << ω0. В этом случае
|
|
|
ωL − |
1 |
2 |
|
1 |
|
|
ωL − |
1 |
|
|
π |
|
Z |
|
= R2 + |
≈ |
, |
ϕ = rctg |
ωC |
|
≈ − |
, |
||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
ωC |
|
ωC |
|
|
R |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Основы теории цепей. Конспект лекций |
-186- |

ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в цепь RLC гармонического напряжения
так как ωL |
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ранее было получено выражение для тока в контуре |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
i(t )= I |
|
|
cos |
(ωt + ψ −ϕ)− I |
|
|
ω0 |
cos( |
ψ −ϕ)e−δt sin (ω |
t + ϕ |
|
)+ |
|||||||||||||||||||||||||
m |
m ω |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СВ |
C |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
ωL |
sin (ψ −ϕ) |
|
e |
−δt |
|
|
t. |
|
|
|
|
||||||||||||
|
|
|
|
|
+ |
|
|
m |
|
cos |
ψ + |
|
|
|
|
|
|
|
sin ω |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ω |
|
L |
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
СВ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
СВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При ω ≈ ω |
|
|
ϕ |
= arctg ωСВ |
≈ π и ток |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
СВ |
0 |
|
|
|
C |
|
|
|
|
|
|
δ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i(t ) |
≈ I |
|
|
cos |
|
ωt |
+ ψ + π − I |
|
|
ω0 |
|
cos |
ψ + |
π e−δt sin |
|
ω |
t + |
π |
+ |
||||||||||||||||||
m |
|
m |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
ωСВ |
|
|
|
|
|
|
|
|
|
|
|
СВ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
E |
m |
|
|
|
|
ωL |
|
|
|
|
π |
|
|
−δt |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
+ |
|
|
|
cos |
ψ + |
|
|
|
|
sin ψ + |
|
e |
|
|
sin ωСВt. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
ωСВL |
|
Z |
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Проведя несложные преобразования, получим
i(t ) ≈ −Im sin (ωt + ψ)+ Im sin ψe−δt cosω0t +
+ Em [cosψ + ωLωC+cosψ]e−δt sin ω0t = ω0L
= −I |
m |
sin |
(ωt |
+ ψ)+ I |
m |
sin ψe−δt cosω t + |
|||
|
|
|
|
|
|
|
0 |
||
|
|
Im |
|
|
|
2 |
|
|
|
+ |
|
|
1− |
ω |
cosψ e−δt sin ω0t. |
||||
|
|
|
2 |
||||||
|
ω0LωC |
|
|
|
|
||||
|
|
ω0 |
|
|
|||||
При ω >> ω0 и ψ = 0 (напряжение источника ЭДС в момент включения проходит через максимум, равный Em) получим
i(t )= −Im sin ωt + Im ωω0 e−δt sin ω0t .
Основы теории цепей. Конспект лекций |
-187- |
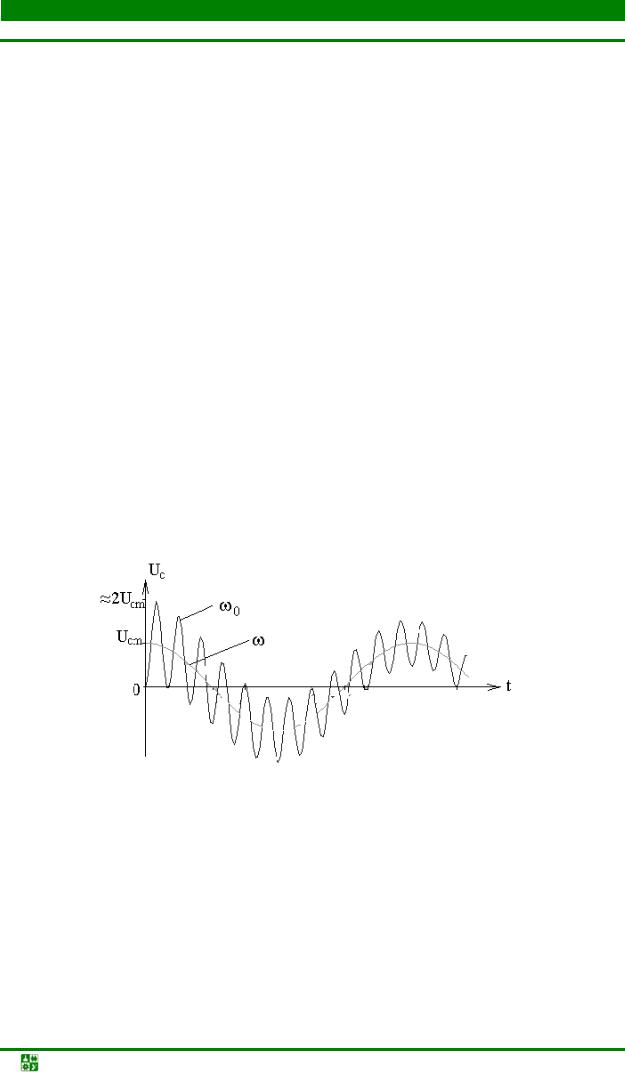
ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в цепь RLC гармонического напряжения
Если δt << 1, то максимальное значение тока в начальный период пре-
вышает амплитуду принужденного тока почти в |
ω0 |
1 раз. Это явление но- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
сит название сверхтока. В этом случае напряжение на конденсаторе |
||||||||||||||||
U |
|
(t )= |
1 |
|
i(t )dt = |
1 |
|
|
− I |
|
sin ωt + I |
|
ω0 e− δt sin ω t |
dt = |
||
C |
C ∫ |
C ∫ |
|
m |
m |
|||||||||||
|
|
|
|
|
ω |
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
Im |
|
cosωt + I |
|
|
|
ωe−δt |
|
(−δsin ω t −ω |
cosω t ). |
|||||
|
m ω0 |
(δ2 + ω02 ) |
|||||||||||||
|
ωC |
|
|
|
|
|
0 0 |
0 |
|||||||
|
|
|
|
ax |
|
|
|
|
|
|
eax |
|
|
|
|
|
|
∫ |
e |
|
sin bxdx = |
|
|
(asin bx −bcosbx) . |
|||||||
|
|
|
a2 +b2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При δ << ω0 и UCm = |
Im |
|
|
|
|
|
|
|
|
|
|
||||
ωC |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
UC(t) ≈ UCmcosωt – UCme–δtcosω0t.
Начальные максимумы UC(t) примерно в два раза больше амплитуды принужденной составляющей (рис. 20.20).
|
|
|
|
|
UC |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
≈2UCm |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ω0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
UCm |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ω |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 20.20
Если же ω >> ω0, то в контуре с малыми потерями |Z| ωL, φ π/2 и ток
в контуре будет
i(t) = Imsin(ωt – ψ) – Imsinψe–δtcosω0t.
При ψ π/2, т. е. напряжение в момент включения проходит через нуль,
имеем
i(t) ≈ Imcosωt – Ime–δtcosω0t.
Напряжение на емкости
Основы теории цепей. Конспект лекций |
-188- |

ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
Включение в цепь RLC гармонического напряжения
|
C |
|
|
|
|
|
1 |
|
∫ |
|
|
|
|
|
|
1 |
∫ |
( |
|
m |
|
|
|
m |
|
0 |
) |
||||||
U |
|
(t) |
|
= |
|
|
C |
|
|
i(t)dt = |
C |
|
|
|
I |
|
|
|
cosωt − I |
|
e−δt cosω t dt = |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
Im |
|
sin ωt |
+ I |
|
1 |
|
|
|
|
e- δt |
|
|
|
(−δcosω t |
−ω |
sin ω t )= |
||||||||||||||||
ωC |
m C δ2 + ω2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
= |
Im |
|
sin ωt − |
|
Im |
|
e−δt sin ω t, |
(δ |
ω ). |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
ω0C |
|
|
|
|
|
|
0 |
|
|
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
ax |
|
|
|
|
|
|
|
|
|
|
|
eax |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
∫ |
e |
|
|
cosbxdx = |
|
|
|
|
|
|
|
|
|
|
(a cosbx +bsin bx) . |
|
||||||||||||||
|
|
|
|
|
a2 +b2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Отсюда следует, что в начальный период времени, когда δt << 1, максимальное значение тока в контуре примерно в два раза больше принужденной составляющей (аналогично кривым UC(t) на рис. 20.20). Максимумы напряжения на емкости оказываются много больше амплитуды принужденной составляющей, так как
Im |
|
Im |
=UCm. |
|
ω0C |
ωC |
|||
|
|
Таким образом, при включении гармонической ЭДС в контуре может появиться напряжение очень большой величины (явление перенапряжения). В результате явлений сверхтока и перенапряжения в цепи возникает опасность электрического пробоя конденсатора или пробоя изоляции катушки.
Контрольныевопросы
1.При каких условиях в RLC-цепи возникает апериодический процесс?
2.При каких условиях в RLC-цепи возникает колебательный процесс?
3.Как в плоскости комплексного переменного располагаются корни характеристического уравнения RLC-цепи?
4.Чем определяется скорость нарастания колебаний в RLC-цепи?
5.При каких условиях в RLC-цепи возникают биения?
Основы теории цепей. Конспект лекций |
-189- |

ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Общая схема применения классического метода. Примеры применения классического метода расчета переходных процессов.
Общаясхемапримененияклассическогометода.
Классическим называют метод расчета, в котором решение системы уравнений, описывающих переходные процессы в разветвленной цепи, находят в виде суммы принужденного и свободного решений (составляющих). Определение постоянных интегрирования, входящих в выражения для свободных составляющих, производят путем совместного решения системы алгебраических уравнений по известным значениям корней характеристического уравнения, а также по известным значениям свободных составляющих токов (или напряжений) и их производных по времени, взятых при
t = 0, т. е.
i(t) = iПР(t) + iCB(t), |
U(t) = UПР(t) + UCВ(t). |
Поскольку принужденная составляющая определяется воздействующей ЭДС, то для ее нахождения можно использовать все известные методы расчета цепи в установившемся режиме, метод уравнений Кирхгофа, метод контурных токов, метод узловых потенциалов, метод эквивалентного генератора и др.
Свободные составляющие токов и напряжений представляют собой общее решение системы однородных линейных дифференциальных уравнений, составленных для цепи после коммутации. Свободные составляющие токов (напряжений) в цепи могут быть представлены в виде суммы экспоненциальных слагаемых, число членов которой равно числу корней характеристического уравнения.
Для заданной цепи степень характеристического уравнения не зависит от выбора контуров, для которых составляются уравнения по второму закону Кирхгофа. Степень характеристического уравнения равна числу независимых начальных условий в послекоммутационной цепи после максимального ее упрощения (параллельно соединенные емкости заменяются одной емкостью, последовательно включенные индуктивности также заменяются одной индуктивностью и т. д.). Система уравнений составляется обычным образом: а) выбираются положительные направления токов в ветвях и б) по первому и второму законам Кирхгофа составляются уравнения. Если выбрать контуры
Основы теории цепей. Конспект лекций |
-190- |

ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Общая схема применения классического метода
так, чтобы порядок дифференциальных уравнений был наименьшим, то степень характеристического уравнения не будет превышать суммы порядков исходных уравнений системы. При этом совершенно не обязательно приводить систему дифференциальных уравнений к одному уравнению относительно одной неизвестной функции (току или напряжению).
Для свободных составляющих токов в ветвях в уравнениях, составленных по второму закону Кирхгофа, следует освободиться от принуждающих ЭДС, т. е. взять правые части, равные нулю.
Поскольку решение для свободных составляющих ищется в виде
iСВ (t )= Ae |
pt |
|
di |
d (Aept ) |
= iСВ, ∫iСВdt∫Ae |
pt |
dt = |
i |
||
|
, |
СВ |
= |
|
|
СВ |
. |
|||
|
|
dt |
|
|
||||||
|
|
|
dt |
|
|
|
p |
|||
Заменив в исходной системе дифференциальных уравнений
L |
diСВ |
на LpiСВ и |
1 |
∫iСВdt |
на |
1 |
iСВ, |
dt |
C |
pC |
получим систему однородных алгебраических уравнений относительно свободных составляющих токов в ветвях. Решив эту систему, получим для тока в k-й ветви
i |
|
= k , |
kСВ |
|
|
где – определитель системы; k |
– определитель, полученный заменой k-го |
|
столбца в определителе системы на столбец из правых частей уравнений, равных нулю, т. е. k = 0. А это значит, что система уравнений имеет решение, отличное от нулевого решения, если определитель = 0.
Уравнение (p) = 0 называют характеристическим уравнением систе-
мы. Единственным неизвестным в нем является р.
Корни характеристического уравнения могут быть действительными и комплексными. Если корни комплексные, то они образуют комплексносопряженные пары. Действительные части всех корней отрицательны, что физически обусловлено затуханием свободных составляющих в пассивных цепях с течением времени.
Пусть характеристическое уравнение имеет n корней, тогда
n
iСВ (t )= ∑Ak epkt ,
k=1
где Ak – постоянная интегрирования.
Основы теории цепей. Конспект лекций |
-191- |

ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Общая схема применения классического метода
Число слагаемых в последнем выражении определяется степенью характеристического уравнения: а) уравнение первой степени имеет только один действительный и отрицательный корень (цепи первого порядка RL и RC); б) уравнение второй степени может иметь два действительных отрицательных неравных корня (апериодический режим в RLC-цепи), два действительных равных отрицательных корня (критический режим) либо два ком- плексно-сопряженных корня с отрицательной действительной частью (колебательный режим в RLC-цепи). В последнем случае свободная составляющая имеет вид
i(t ) = A1ep1t + A2ep2t = A1e−δte jωkt + A2e−δte− jωkt =
=e−δt (A1 cosωkt + A1 j sin ωkt + A2 cosωkt − A2 j sin ωkt )=
=e−δt (A1 + A2 )cosωkt + j (A1 − A2 )sin ωkt =
= e−δt (M cosωkt + N sin ωkt )= Ae−δt sin (ωkt + γ),
где A = M 2 + N 2 , γ = arctg |
N |
. |
|
||
|
M |
|
В общем случае сложная цепь может иметь все три вида корней характеристического уравнения и решение для свободных составляющих представляет собой совокупность экспонент и затухающих по экспоненте синусоид.
Постоянные интегрирования находятся из системы уравнений, полученной (n – 1)-кратным дифференцированием выражения для свободной составляющей с учетом уравнений Кирхгофа для послекоммутационной цепи при t = 0 и независимых начальных условий, т. е. из решения системы уравнений
iСВ (0)= i(0) |
−iПР (0) |
n |
|||
= ∑Ak ; |
|||||
|
|
|
|
|
k=1 |
|
′ |
′ |
|
′/ |
n |
|
|
||||
iСВ |
(0)= i |
(0)−iПР (0)= ∑pk Ak ; |
|||
|
|
|
|
|
k=1 |
|
|
− − − − − − − − − − − − − − − − − |
|||
|
|
|
|
|
|
|
|
|
|
|
n |
iСВ(n−1) (0)= i(n−1) (0)−iПР(n-1) (0)= ∑pkn−1Ak . |
|||||
|
|
|
|
|
k=1 |
Основы теории цепей. Конспект лекций |
-192- |
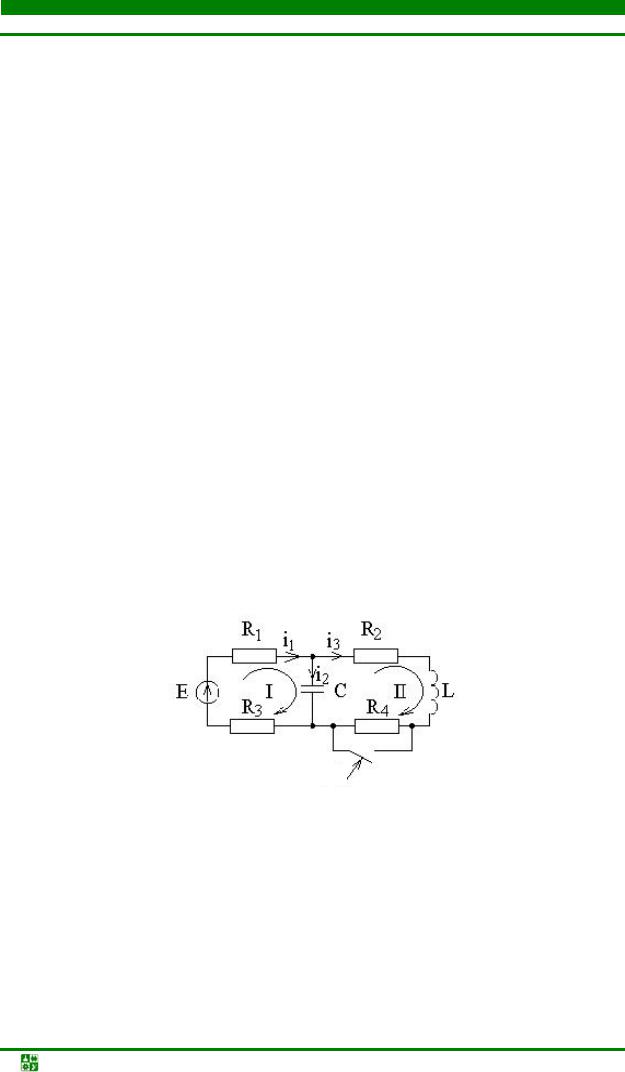
ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Общая схема применения классического метода
Определив Аk, можем записать полное выражение для искомой величи-
ны i(t) = iПР(t) + iCB(t), U(t) = UПР(t) + UCB(t).
Таким образом, расчет переходных процессов классическим методом производится в следующем порядке:
1. Рассчитывают режим до коммутации, где находят значения токов в индуктивностях и напряжений на емкостях в момент времени t = 0. Используя законы коммутации, находят независимые начальные усло-
вия iL(0) и UC(0).
2.Производят расчет принужденного режима после коммутации.
3.Составляют систему уравнений Кирхгофа для цепи после коммутации.
4.Находят общее решение системы однородных уравнений (определяется характеристическое уравнение и находятся его корни). Определяют зависимые начальные условия из независимых начальных условий и системы уравнений Кирхгофа для t = 0.
5.Определяют постоянные интегрирования по начальным условиям.
6. Записывают полное решение в виде i(t) = iПР(t) + iCB(t), U(t) = = UПР(t) + UCB(t).
Примерыпримененияклассическогометода расчетапереходныхпроцессов.
Пример 1. В цепи (рис. 21.1) действует постоянная ЭДС Е = 100 В.
|
|
R1 |
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
i3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
i1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
I |
|
C |
|
|
L |
|||||||||||
E |
|
|
|
II |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
R3 |
|
|
|
|
|
|
|
|
|
|
|
|
R4 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
t = 0
Рис. 21.1
R1 = 10 Ом, R2 = 20 Ом, R3 = 50 Ом, R4 = 20 Ом, L = 1м ГН, C = 100 мкФ.
Требуется определить закономерность изменения во времени тока iL = i3. Решение. 1. Независимыми начальными условиями будут ток iL(0–) =
= i3(0–) и напряжение на емкости UC(0–), определим их:
Основы теории цепей. Конспект лекций |
-193- |

ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Примеры применения классического метода расчета переходных процессов
iL (0 |
−)= |
|
|
E |
= |
|
|
100 |
|
=1 A; |
|
R1 |
+ R2 |
+ R3 + R4 |
10 |
+ 20 +50 |
+ 20 |
||||||
|
|
|
|
||||||||
UС (0 −)= iL (0 −) (R2 + R4 )=1 40 = 40 B.
2. Составим систему уравнений по законам Кирхгофа для послекоммутационной схемы:
E = (R1 + R3 )i1 + C1 ∫i2dt,
1 di0 = −C ∫i2dt + R2i3 + L dt3 ,
0 = i1 −i2 −i3.
Для свободных составляющих токов эта система имеет вид
0 |
= (R + R )i |
+ |
1 |
|
i dt, |
|
||||||
C ∫ |
|
|||||||||||
|
1 |
|
3 |
1CB |
|
|
2CB |
|
||||
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
di3CB |
|
|
0 |
= − |
|
i |
dt + R i |
|
+ L |
, |
|||||
C ∫ |
|
|
||||||||||
|
|
2CB |
|
2 3CB |
|
dt |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
0 |
= i1CB −i2CB −i3CB. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Произведя алгебраизацию системы, получим:
0 = (R1 + R3 )i1CB + pC1 i2CB ,
0 = − pC1 i2CB +(R2 + Lp)i3CB ,
0 = i1CB −i2CB −i3CB.
Данная система имеет решение, отличное от нулевого решения, если определитель системы равен нулю, т. е.
Основы теории цепей. Конспект лекций |
-194- |

ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Примеры применения классического метода расчета переходных процессов
|
R1 + R3 |
|
1 |
|
|
0 |
|
|
|
|
pC |
|
|
||||
|
|
|
|
|
|
|||
(p)= |
0 |
− |
1 |
R |
+ Lp |
= 0. |
||
|
||||||||
|
|
|
|
pC |
2 |
|
||
|
|
|
|
|
|
|
||
|
1 |
|
−1 |
|
−1 |
|
||
|
|
|
|
|
|
|
|
|
Раскрывая определитель, получим характеристическое уравнение второй степени:
(R1 + R3 ) pC1 + pC1 (R2 + Lp)+(R1 + R3 )(R2 + Lp)= 0;
(R |
+ R )LCp2 +(R |
+ R )R pC |
+ Lp + R |
+ R |
+ R |
= 0; |
||||||
1 |
3 |
1 |
|
3 |
|
2 |
|
|
1 |
3 |
2 |
|
|
60 10−3 10−4 p2 +(60 20 10−4 +10−3 )p +80 = 0; |
|||||||||||
|
p1 = −680, |
|
p2 = −19480. |
|
|
|
||||||
3. Общее решение для тока iLCB(t) имеет вид |
|
|
|
|||||||||
|
i |
LСВ |
(t ) |
= A ep1t |
|
+ A e p2t . |
|
|
|
|||
|
|
|
|
1 |
|
|
2 |
|
|
|
||
4. Найдем принужденную составляющую тока: |
|
|
|
|||||||||
|
i |
= |
|
|
E |
|
|
= |
100 =1,25 A . |
|
||
|
R + R + R |
|
|
|||||||||
|
LПР |
|
|
|
80 |
|
|
|
||||
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
5. На основании законов коммутации iL(0–) = iL(0) и UC(0–) = UC(0) оп-
ределим производную didtL в момент времени t = 0 (зависимое начальное ус-
ловие). Из второго уравнения системы для t = 0 следует
−UС (0)+ R2i3 (0)+ L didt3 (0)= 0,
отсюда
Основы теории цепей. Конспект лекций |
-195- |
ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Примеры применения классического метода расчета переходных процессов
|
di3 |
(0)= |
UС (0)− R2i3 (0) |
= 40 − 20 |
|
= 20 103 В/Гн. |
||||||||||||
|
dt |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
L |
|
|
|
|
10−3 |
|
|
|
|
|
6. Определим постоянные интегрирования A1 и A2: |
||||||||||||||||||
|
|
|
i |
|
(t ) = i |
|
+ |
A e p1t |
+ A ep2t , |
|
||||||||
|
|
|
3 |
|
3ПР |
|
1 |
2 |
|
|
|
|
||||||
|
|
di |
|
|
di |
|
|
|
p t |
|
|
|
p t |
|
||||
|
|
|
|
|
3 |
|
= |
3ПР |
+ p A e 1 |
+ p A e |
2 |
, |
||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
dt |
|
1 |
1 |
2 |
2 |
|
|
|||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
i |
(0) = i |
(0) = i |
+ A + |
A , |
|
||||||||||
|
|
|
|
3 |
|
|
L |
|
|
3ПР |
1 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
di3 (0)= 0 + p A + p A |
|
, |
|
|
|||||||
|
|
|
|
|
|
|
dt |
|
|
1 1 |
2 2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1−1,25 = A1 + A2 , |
|
|
|
|
||||||
|
|
|
20 103 = −680A −19480A |
, |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
||
отсюда A1 = 0,805; A2= – 1,055.
7. Запишем выражение для искомого тока в виде
i3(t) = i3ПР(t) + i3CB(t) = 1,25 + 0,805e–680t – 1,055e–19480t.
i3(t), A
i3(t)
i3ПР
0,805 е–680t
t, мс
1,0
–1,055 е–19480t
Рис. 21.2
Графики принужденной, свободных оставляющих и полного тока приведены на рис. 21.2.
Пример 2. Решить задачу, приведенную в примере 1, заменив постоянную ЭДС гармонической
e(t) = 100cos(ωt + 60°), где ω = 10000P/C.
Основы теории цепей. Конспект лекций |
-196- |

ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Примеры применения классического метода расчета переходных процессов
Решение. 1. Определим независимые начальные условия UC(0–) и iL(0). На основании закона Ома для докоммутационной цепи имеем
|
|
|
UC |
(0 −)= |
|
E |
|
Z, |
|
|
||||||
|
|
|
R1 |
+ R3 |
+ Z |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где Z = |
R2 + R4 + jωL |
|
|
|
|
. |
|
|
|
|
|
|
|
|
||
1+(R |
+ R + jωL) jωC |
|
|
|
|
|
|
|
|
|||||||
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив значения R, L, C, E, получим |
|
|
|
|
||||||||||||
|
|
Z = |
|
20 + 20 + j10410−3 |
|
≈1e |
−89° |
, |
||||||||
|
|
1+(20 + 20 + j10410−3 ) j10410−4 |
|
|||||||||||||
|
|
UC (0 −)= |
|
|
|
100e j60° |
|
1e−89° |
=1,64e j150°, |
|
||||||
|
|
10 +50 +1e−89° |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
IL (0 −)= |
|
|
UC (0 −) |
|
= 0,04e j137°. |
|
|
||||||
|
|
|
|
R2 + R4 + jωL |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Мгновенные значения напряжения и тока |
|
|
|
|
||||||||||||
UC(t) = 1,64cos(ωt + 150°), |
|
|
|
iL(t) = 0,04cos(ωt + 137°), |
|
|
||||||||||
для t = 0 |
UC(0–) = 1,64cos150° = –1,42 В, |
|
|
|
|
|
|
|||||||||
iL(0–) = 0,04cos137° = 0,03 A.
Система уравнений Кирхгофа для цепи после коммутации не зависит от вида ЭДС, следовательно, можно использовать систему из примера 1. Характеристическое уравнение системы и общее решение для тока имеет такой же вид, как и в первом примере.
Найдем принужденную составляющую тока i3ПР. Как и в цепи до коммутации
|
|
ILПР = |
E Z′ |
|
1 |
, |
|
|
|
R1 + R3 + Z′ |
R2 + jωL |
||||
где Z′ = |
|
R2 + jωL |
|
|
|
|
|
|
|
. |
|
|
|
|
|
1 |
+(R + jωL) jωC |
|
|
|
|
||
|
|
2 |
|
|
|
|
|
Подставив значения R, L, C, E, получим
Основы теории цепей. Конспект лекций |
-197- |

ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Примеры применения классического метода расчета переходных процессов
ILПР = 0,076 e− j53°, iLПР (t ) = 0,076cos(ωt −53°),
для t = 0 iLПР(0) = 0,04cos(–53°) = 0, 046 А.
Зависимое начальное условие |
|
di3 |
в момент t = 0 определим из второго |
|||||||||||||||||||||
|
dt |
|||||||||||||||||||||||
уравнения системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
di3 |
(0)= |
UC (0)− R2i3 (0) |
|
= −1,42 − 20 0,03 |
= −820 В/Гн. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
dt |
|
|
|
L |
|
|
|
|
|
|
|
10−3 |
|
|
|
||||||||
Определим постоянные интегрирования А1 и А2: |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
i |
(t ) = i |
|
+ A e p1t |
+ A ep2t , |
|
|
|||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
3ПР |
|
1 |
|
2 |
|
|
|
|||||
|
|
|
|
|
|
di |
|
|
|
|
di |
|
|
p t |
|
|
p t |
|
||||||
|
|
|
|
|
|
|
3 |
|
= |
3ПР |
+ p A e 1 |
+ p A e 2 |
|
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
1 |
1 |
|
2 2 |
|
|
||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
di3ПР |
|
= −ω 0,076sin (ωt −53°), |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
для t = 0 |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
di3ПР |
(0)= −104 0,076sin (−53°)= 610 B/Гн. |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i ( |
0)= i |
|
(0)= i |
|
(0) |
+ A |
+ A |
, |
|
|
||||||||||||
|
|
3 |
|
|
|
L |
|
|
|
|
|
3ПР |
|
1 |
|
2 |
|
|
|
|||||
|
|
di3 |
(0)= |
di3ПР |
(0) |
+ p A + p |
A |
, |
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
1 |
1 |
|
2 2 |
|
|
|||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
−0,3 = 0,046 + A1 + A2 , |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
−820 = 610 −680A1 −19480A2 , |
|
|
|
|||||||||||||||||||
отсюда А1 = –0,1548, |
|
А2 = 0,0788. |
|
|
|
|
|
|
|
|
||||||||||||||
Полное выражение для искомого тока: |
|
|
|
|
||||||||||||||||||||
i3(t) = 0,076cos(ωt – 53°) = –0,546e–680t + 0,0788e–19480t.
Графики принужденной и свободных составляющих тока приведены на рис. 21.3.
Основы теории цепей. Конспект лекций |
-198- |
ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Примеры применения классического метода расчета переходных процессов
i3(t), A
0,0788 е–19480t i3ПР
t, мс
i3(t)
–0,1548 е–680t
Рис. 21.3
Следует отметить, что довольно часто при нахождении постоянных интегрирования можно в системе уравнений использовать не производную искомой величины по времени, а интеграл. Например, при нахождении тока через емкость имеем iC(0) = iCПР(0) + А1 + А2.
Поскольку в систему уравнений, составленных по законам Кирхгофа, производная di/dt не входит, используем интеграл от тока по времени. Действительно,
|
|
|
|
|
1 |
|
|
∫iC dt =UC , |
|
для |
|
iCСВ = A1ep1t + A2e p2t , |
||||||||||||||||
|
|
|
|
|
C |
|
|
|||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
i |
dt |
= |
|
1 |
∫ |
A e |
p1t |
+ A e |
p2t |
dt |
=U |
CСВ |
(t ), , |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
C |
|
|
∫ CСВ |
|
|
|
|
C |
( 1 |
|
|
2 |
|
) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
A ep1t |
1 |
|
|
A ep2t |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
+ |
|
|
|
|
|
2 |
|
=UCСВ (t ), |
|
|
|
|
||||
|
|
|
|
|
C |
|
p1 |
|
|
C |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
||||||||
для t = 0 |
1 |
|
A1 |
+ |
|
1 |
|
A2 |
=UCСВ (0)=UC (0 −)−UCПР (0). |
|
||||||||||||||||||
|
|
C p2 |
|
|||||||||||||||||||||||||
|
C p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Такимобразом, системауравненийдлярасчетапостоянныхинтегрирования
i |
(0) |
−i |
(0) = A |
+ A , |
|
|
|
|
||||
C |
|
CПР |
1 |
|
2 |
|
|
|
|
|
||
UC (0 −)−UCПР (0) |
= |
1 |
|
A1 |
+ |
1 |
|
A2 |
. |
|||
|
|
|
|
|||||||||
|
|
|
|
|
C p1 |
C p2 |
||||||
Основы теории цепей. Конспект лекций |
-199- |

ЛЕКЦИЯ 21. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАЗВЕТВЛЕННОЙ ЦЕПИ
Примеры применения классического метода расчета переходных процессов
Аналогичное решение можно предложить, если в задаче необходимо найти напряжение на индуктивности:
|
|
|
|
|
|
|
|
|
|
i |
|
(t )= |
1 |
|
U dt , |
||||||
|
|
|
|
|
|
|
|
|
|
L ∫ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
L |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
U |
L |
(0)−U |
LПР |
(0) = A + |
A , |
|
|
|
|
|
|
|||||||||
тогда |
|
|
|
|
1 |
1 |
|
|
|
2 |
|
A |
|
||||||||
|
i |
(0 −)−i |
|
(0)= |
|
A |
|
|
1 |
|
|
||||||||||
|
|
|
|
|
1 |
|
+ |
|
|
|
2 |
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
L |
|
LПР |
|
|
L p1 |
|
|
|
L p2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Контрольныевопросы
1.Какой метод расчета переходных процессов называют классическим?
2.Какое уравнение называют характеристическим уравнением системы?
3.Каковы особенности корней характеристического уравнения?
4.Каковы основные недостатки классического метод расчета переходных процессов?
Основы теории цепей. Конспект лекций |
-200- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Преобразование Лапласа. Изображение простейших функций. Основные свойства преобразования Лапласа. Нахождение оригинала по изображению. Законы Ома и Кирхгофа в операторной форме. Последовательность расчета в операторном методе.
Расчет переходных процессов в сложных цепях классическим методом очень часто затруднен нахождением постоянных интегрирования. В связи с этим был разработан операторный метод расчета, основанный на понятии изображения функций времени. В операторном методе каждой функции времени соответствует функция новой комплексной переменной p = c + jω и наоборот функции от р отвечает определенная функция времени t. Переход от одной функции к другой осуществляется с помощью преобразования Лапласа.
Данный метод облегчает решение системы интегродифференциальных уравнений, составленных для цепи по законам Кирхгофа, а также позволяет освободиться от нахождения постоянных интегрирования путем введения начальных условий в уравнения исходной системы.
Таким образом, идея метода заключается в том, что из области действительного переменного t решение переносится в область комплексного переменного p = c + jω, где операции дифференцирования и интегрирования более просты.
Операторный метод расчета сводится к четырем последовательным этапам.
1.От искомой функции f(t), называемой оригиналом, переходят с помощью преобразования Лапласа к функции комплексного переменного р. Новую функцию обозначают через F(p) и называют изображением функции f(t).
2.Систему уравнений Кирхгофа для оригиналов, согласно правилам преобразования функций, их производных и интегралов преобразуют в операторные алгебраические уравнения для изображений.
3.Полученные операторные уравнения решают относительно F(p).
4.От найденного изображения F(p) переходят к оригиналу f(t), который и является искомой функцией.
ПреобразованиеЛапласа.
Пусть дана некоторая функция действительной переменной f(t) (напряжение или ток), удовлетворяющая следующим условиям:
Основы теории цепей. Конспект лекций |
-201- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Преобразование Лапласа
1.Функция f(t) со своими производными непрерывна на всей оси t. Возможны исключения, а именно: наличие конечного числа точек разрыва первого рода.
2.Функция f(t) равна нулю при отрицательных значениях t:
f(t) = 0 при t < 0.
3. Функция f(t) возрастает не быстрее некоторой показательной функции: существуют постоянные числа М > 0 и C0 такие, что для всех t
f (t) |≤ MeС0t .
Следует заметить, что практически во всех инженерных задачах функция f(t) отвечает поставленным условиям.
Из курса математики известно, что если f(t) имеет ограниченный рост, то интеграл
∞
∫ f (t )e− pt dt
0
сходится абсолютно и является аналитической функцией комплексного переменного p = c + jω в полуплоскости Rep = с > c0 (рис. 22.1).
|
|
|
|
jω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(t) |
|
|
|
|
|
|
|
|
|
|
|
+c |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|||
|
|
0 |
|
|
|
c0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||
|
|
|
|
|
Рис. 22.1 |
|
|
|
|
|
Рис. 22.2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (p)= ∫ f |
(t )e− pt dt , |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
где f(t) – оригинал; F(p) – изображение: |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
F(p) |
f(t), f(t) |
|
F(p), |
|
|
|
||||
где |
– символ соответствия между оригиналом и изображением по Лапласу. |
||||||||||||||||||
Основы теории цепей. Конспект лекций |
-202- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Изображениепростейшихфункций.
1. Изображение постоянной величины (рис. 22.2)
|
f (t ) |
0 |
при |
|
= |
при |
|
|
|
E |
|
∞ |
∞ |
|
|
F (p)= ∫ f (t )e− pt dt =∫E e− pt dt = − |
|||
0 |
0 |
|
|
t < 0, |
|
|
|
|
|
|
||
t > 0. |
|
|
|
|
|
|
||
Ee− pt |
|
∞ |
= |
E |
, |
E i=i |
E |
. |
|
||||||||
p |
|
0 |
p |
p |
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Зная изображение постоянной, можно записать изображение единичной функции
|
0 |
при |
t < 0, |
|
|
1 |
|
|
|
|
|
|
|
1(t )= |
|
|
1 i=i |
|
. |
|
|
|
|
||
|
при |
t > 0, |
|
|
|
|
|
|||||
|
1 |
|
|
p |
|
|
|
|
||||
2. Изображение показательной функции f (t )= eαt |
|
|
|
|
||||||||
∞ |
∞ |
∞ |
|
|
1 |
|
∞ |
1 |
|
|||
|
|
|
|
|||||||||
F (p)= ∫ f (t )e− pt dt =∫eαte− pt dt =∫e−t(p−α)dt = − |
e−t(p−α) |
= |
, |
|||||||||
p −α |
p −α |
|||||||||||
0 |
0 |
0 |
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|||||
eαt i=i p −1 α при Rep > Reα.
Положив в последней формуле α = jω, получим
f (t )= e jωt i=i p −1 jω.
Далее можно найти изображение комплекса гармонического тока и напряжения
Ime jωt+ψ = Ime jωt |
i=i |
Im |
, Ume jωt |
i=i |
Um |
. |
|
p − jω |
p − jω |
||||||
|
|
|
|
|
ОсновныесвойствапреобразованияЛапласа.
Очевидно, что соответствие между оригиналом и изображением взаимно однозначны, т. е. каждой функции f(t) соответствует одна вполне определенная функция F(p) и наоборот.
Основы теории цепей. Конспект лекций |
-203- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Основные свойства преобразования Лапласа
Свойство линейности. При умножении оригинала на постоянную величину на ту же постоянную величину умножается и изображение
а f(t) |
а F(p). |
Действительно, |
|
∞ |
∞ |
F (p)= ∫a f (t )e− pt dt = a∫ f (t )e− pt dt = aF (p). |
|
0 |
0 |
Если оригинал представлен суммой функций, то изображение этой суммы равно сумме изображений этих функций (свойство линейности преобразования Лапласа: изображение линейной комбинации функций есть линейная комбинация изображений)
n
∑ak fk (t )
k=1
n
i=i ∑ak Fk (p).
k=1
Теорема дифференцирования. Допустим, что некоторая функция f(t) имеет изображение F(p), требуется найти изображение производной этой функции. Пусть f΄(t) = φ(t). Найти Ф(р)  φ(t).
φ(t).
|
|
∞ |
∞ |
|
Ф(p)= ∫φ(t )e− pt dt =∫ f ′(t )e− pt dt . |
||||
0 |
0 |
|
||
Интегрируя по частям, получим |
|
|
||
|
|
0∞ −(−p) |
∞ |
|
Ф( p) = e− pt f (t ) |
|
∫ f (t )e− pt dt = − f (0)+ pF (p), |
||
|
||||
|
|
|
0 |
|
(∫VdU =VU − ∫UdV , |
V =e− pt , |
dU = f ′(t )dt, |
||
dV = −pe- pt , U = ∫ f ′(t )dt = f (t )) |
f ′(t )i=i pF (p)− f (0). |
|||
Вычисление производной при нулевых начальных условиях [f(0) = 0] соответствует умножению изображения функции на множитель p:
f ′(t ) i=i pF (p), f k (t ) i=i pk F (p).
Основы теории цепей. Конспект лекций |
-204- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Основные свойства преобразования Лапласа
Теорема интегрирования. Известно изображение некоторой функции f(t). Требуется определить изображение функции, являющейся интегралом
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
функции f(t). Пусть ψ(t )= ∫ f |
(t )dt , тогда f (t ) = ψ′(t )i=i pψ(p)−ψ(0), |
|||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
если |
ψ(0)= 0 |
|
0 |
|
|
, то |
f (t )= ψ′(t ) |
=i |
pψ(p), |
|||||||
|
∫ |
f (t )dt = 0 |
||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( f )i=i F (p), F (p)= pψ(p), |
ψ(p)= |
F (p) |
, |
t |
f (t )dt i=i |
F (p) |
. |
||||||||
|
|
|
∫ |
|
||||||||||||
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
p |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Многократному интегрированию соответствует общее выражение |
||||||||||||||||
|
|
|
|
t |
dt t |
dt…t |
f (t )dt i=i |
F (p) |
. |
|
|
|
|
|||
|
|
|
|
∫ |
|
|
|
|
|
|||||||
|
|
|
|
∫ |
∫ |
|
|
pn |
|
|
|
|
||||
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
n
Теорема запаздывания. Теорема позволяет определить изображение функции f(t – t1), отличающейся от функции f(t) тем, что она сдвинута вправо вдоль оси времени на t1 (рис. 22.3)
0 |
|
) |
при |
t < t1, |
f (t −t1 )= f (t −t |
при |
t > t . |
||
|
1 |
|
|
1 |
f(t)
f(t) |
|
f(t – t1) |
|
|
|
|
|
|
|
t |
|
|
|
|
|
t1 |
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
||
Рис. 22.3 |
|
|
|
|||||
|
|
|
|
|
|
|||
|
∞ |
|
|
|
∞ |
|||
Ф(p)= ∫ f (t −t1 )e− pt dt = ∫ f (t −t1 )e− pt dt , |
||||||||
0 |
|
|
|
t1 |
||||
так как в интервале (0 – t1) функция f(t – t1) = 0.
Основы теории цепей. Конспект лекций |
-205- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Основные свойства преобразования Лапласа
Введем новую переменную τ = t – t1, тогда t = τ + t1, dt = dτ.
∞ |
∞ |
Ф(p)= ∫ f (t −t1 )e− pt dt = ∫ f (τ)e− p(τ+t1)dτ = |
|
t1 |
0 |
∞
= e− pt1 ∫ f (τ)e− pτdτ = e− pt1 F (p).
0
Таким образом, запаздывание функции на время t1 соответствует ум-
ножению ее изображения на e− pt1 .
Теорема смещения. Теорема смещения позволяет определить, как изменяется изображение при умножении оригинала на показательную функцию e±αt, где α – постоянное число.
Пусть новая функция имеет вид ψ(t) = f(t)e±αt.
Изображение
∞ |
∞ |
Ф(p)= ∫ψ(t )e− pt dt = ∫ f (t )e−(p α)t dt = F (p α). |
|
0 |
0 |
Таким образом, умножение временной функции на экспоненциальный множитель приводит к «смещению» в области изображений независимой переменной p на p α.
Теорему смещения очень удобно применять при определении изображения экспоненциально убывающих функций. Например, необходимо найти изображение функции ψ(t) = sinωte–αt.
Выше было показано, что Ime jωt+ψ = Ime jωt |
i=i |
|
|
|
|
Im |
|
, тогда |
||||||||
|
|
|
p − jω |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
e jωt = cosωt + j sin ωt i=i |
1 |
|
|
|
|
|
= |
|
p + jω |
. |
||||||
p − jω |
|
2 2 |
||||||||||||||
|
|
|
|
|
|
|
p |
+ ω |
||||||||
Разделив вещественную и мнимую части, получим |
|
|
|
|
|
|
|
|
|
|||||||
cosωt i=i |
|
p |
|
, sin ωt i=i |
|
|
ω |
|
. |
|
|
|||||
p |
2 |
2 |
p |
2 |
|
|
2 |
|
|
|||||||
|
+ω |
|
|
|
|
|
|
|
+ω |
|
|
|
||||
Следовательно,
Основы теории цепей. Конспект лекций |
-206- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Основные свойства преобразования Лапласа
ψ(t )sin ωte−αt i=i (p +αω)2 + ω2 .
Теорема умножения изображений (теорема свертки – интеграл Боре-
ля) заключается в следующем. Если
f1(t)  F1(p), f2(t)
F1(p), f2(t)  F2(p),
F2(p),
то
t |
|
t |
|
|
Ф(p)= F1 (p)F2 (p) i=i ∫ f1 |
(τ) f2 |
(t − τ)dτ = ∫ f1 |
(t − τ) f2 |
(τ)dτ. |
0 |
|
0 |
|
|
Таким образом, произведению изображений двух функций соответствует свертка их оригиналов. Теорема свертки широко используется при составлении таблиц операторных соотношений. Если изображение искомой функции может быть представлено в виде произведения двух (или более) сомножителей, то по оригиналам каждого из сомножителей можно вычислить оригинал исходной функции. Например, определим оригинал функции, изображение которой имеет вид
Ф(p)= |
1 |
. |
(p + α)2 |
Изображение Ф(р) можно представить как произведение двух изображений:
Ф(p)= |
1 |
|
|
1 |
= F |
(p)F |
(p), |
||||
|
|
|
|
||||||||
|
|
p + α |
p + α |
|
|
1 |
2 |
|
|||
|
|
|
|
|
|
|
|||||
F |
(p)= F (p)= |
1 |
|
|
=i |
e−αt . |
|
||||
|
p + α |
|
|
|
|||||||
1 |
|
2 |
|
|
|
|
i |
|
|
|
|
Следовательно, |
t |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
||
ψ(t )= ∫e−ατe−α(t−τ)dτ = e−αt ∫dτ = te−αt . |
|||||||||||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
Теорема подобия позволяет определить изображение функции времени при изменении масштаба ее аргумента. Пусть известно изображение функции f(t)  F(p). Определим изображение функции φ(t) = f(at), где а – некоторая положительная постоянная.
F(p). Определим изображение функции φ(t) = f(at), где а – некоторая положительная постоянная.
∞
Ф(p)= ∫ f (at )e− pt dt .
0
Основы теории цепей. Конспект лекций |
-207- |
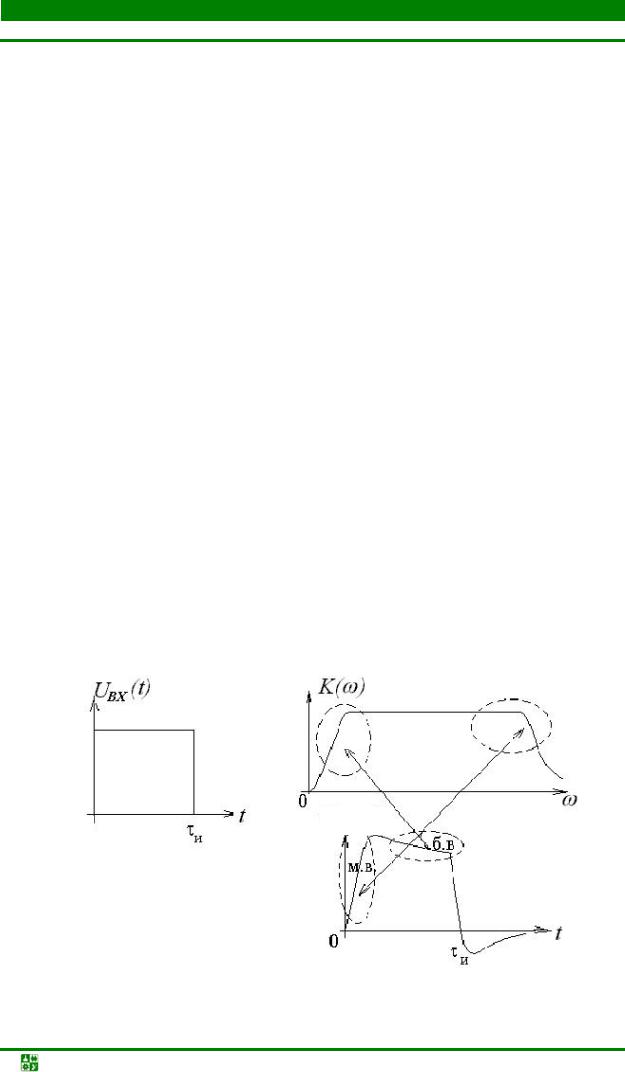
ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Основные свойства преобразования Лапласа
Обозначим at = x, тогда dt = |
1 dx и |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
p |
|
|
|
|
|
|
|
|
|
Ф(p) |
∞ |
f (x)e |
− |
x |
1 |
|
|
|
1 |
p |
|||
= ∫ |
|
|
|
|
|||||||||
|
a |
|
a |
dx = |
a |
F |
|
. |
|||||
|
|
|
|||||||||||
|
0 |
|
|
|
|
|
|
|
a |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончательно имеем |
|
|
|
|
1 |
|
p |
|
|
|
|
||
|
|
(a,t) i=i |
|
|
|
|
|
||||||
|
f |
a |
F |
|
. |
|
|
|
|||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
a |
|
|
|
|
|||
Умножение аргумента оригинала на положительное постоянное число а приводит к делению аргумента изображения и самого изображения на то же число а.
Предельные соотношения устанавливают существование равенства между значениями функции времени и ее изображения в начале координат и в бесконечно удаленной точке.
lim f (t ) = lim pF (p), |
lim f (t ) = lim pF (p). |
||
t→0 |
p→∞ |
t→∞ |
p→0 |
Ниже будет показано, что комплексную переменную р можно рассматривать как обобщенную (комплексную) частоту, мнимая часть которой представляет собой угловую частоту некоторого гармонического колебания, а вещественная характеризует изменение огибающей этого колебания. Приняв вещественную часть р равной нулю, получим из предельных соотношений связь между функцией времени и частотной характеристикой в начале координат и при бесконечных значениях t и jω.
Проиллюстрируем эту связь на примере прохождения импульсного сигнала через усилитель с ограниченной полосой пропускания (рис. 22.4).
UВХ(t) |
|
К(ω) |
|
|
|
НЧ ВЧ
|
|
0 |
|
ω |
|
t |
UВХ(t) |
||||
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
τи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б.в. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
м.в |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τи |
|
|
|
|
Рис. 22.4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
Основы теории цепей. Конспект лекций |
-208- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Основные свойства преобразования Лапласа
Таким образом, характер изменения функции времени в области малых времен определяется частотной характеристикой в области высоких частот и наоборот: характер изменения в области больших времен определяется частотной характеристикой в области низких частот.
Нахождениеоригиналапоизображению.
Существует три способа перехода от изображения к оригиналу. Первый способ – с помощью обратного преобразования Лапласа. Пе-
реход от изображения к оригиналу выполняется с помощью так называемого интеграла Римана – Мелина, являющегося формулой обратного преобразования Лапласа:
|
1 |
c+ j∞ |
|
f (t )= |
∫ F (p)ept dp . |
||
2πj |
|||
|
c− j∞ |
||
|
|
Для того чтобы функция F(p) являлась изображением функции f(t), необходимо выполнение следующих условий: а) F(p) аналитична в полуплос-
c+ j∞
кости Rep > C0; б) стремится к нулю при |p| → ∞; в) интеграл ∫ F (p)dp аб-
c− j∞
солютно сходится.
Практически чаще применяют теорему о вычетах, согласно которой оригиналом F(p) является функция
|
|
f (t ) = ∑Re s F (p)ept |
(t > 0), |
|||
|
|
pk |
|
|
|
|
|
|
f (t )= 0 |
|
|
(t < 0). |
|
Таким образом, |
|
|
|
|||
|
1 |
c+ j∞ |
1 |
∫F (p)ept dp = ∑Re s F (p)ept . |
||
f (t )= |
∫ F (p)ept dp = |
|||||
2πj |
2πj |
|||||
|
|
c− j∞ |
|
|
pk |
|
(Интегрирование вдоль бесконечной прямой, параллельной мнимой оси и расположенной на расстоянии с > C0, заменяется интегрированием по замкнутому контуру, охватывающему все полюсы функции F(p)). Полюсы F(p) есть значения p, при которых F(p) = ∞).
Вычетом функции в некотором полюсе называют величину, на которую уменьшается разделенный на 2πj контурный интеграл от этой функции, когда контур при его стягивании пересечет этот полюс.
Основы теории цепей. Конспект лекций |
-209- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Нахождение оригинала по изображению
Вычисления по последней формуле требуют применения методов теории вычетов, причем во многих случаях это оказывается весьма сложным. Поэтому большое значение имеют теоремы, позволяющие представить изображение в виде суммы более простых слагаемых и тем самым упростить переход от изображения к оригиналу.
Второй способ нахождения оригинала – использование теоремы разложения когда, изображение найдено в виде рациональной дроби:
F (p)= F1 ((p)), где F1(p) и F2(p) – полиномы относительно р. F2 p
Предположим, что знаменатель F2(p) |
имеет n простых корней |
|||||||
p1, p2, ..., pn, тогда общая формула теоремы разложения: |
||||||||
|
F |
(p) |
n |
F (p |
k |
)epkt |
|
|
f (t ) i=i |
1 |
|
i=i ∑ |
1 |
|
. |
||
F2 |
(p) |
F2′(pk ) |
||||||
|
k=1 |
|
||||||
В случае комплексных корней получаются два сопряженных слагаемых, сумма которых равна удвоенному значению действительной части.
Третий способ определения оригинала заключается в использовании таблиц, где приводятся как изображения функций, так и соответствующие им оригиналы. Существуют справочники, содержащие несколько сотен изображений и соответствующих им оригиналов. Следует только изображение привести к табличному виду. При использовании готовых таблиц следует выяснить, с помощью какого преобразования они составлены – Лапласа или Карсона. Если изображение дается по Карсону, то его следует поделить на р для получения изображения по Лапласу.
ЗаконыОмаиКирхгофавоператорнойформе.
Закон Ома. Пусть имеем участок сложной цепи (рис. 22.5), замыкание ключа в которой приводит к переходному процессу.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i4 |
|
|
||
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
R |
|
|
|
C |
|
e(t) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
t = 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
i2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i5 |
||||
|
|
|
i3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Рис. 22.5 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Разность потенциалов между двумя узлами
Основы теории цепей. Конспект лекций |
-210- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Законы Ома и Кирхгофа в операторной форме
U =UR +UL +UC −e(t ), UR = Ri, |
UL = L di |
, |
|
dt |
|
UC =UC (0 −)+ C1 ∫idt.
Тогда
U = Ri + L dtdi +UC (0 −)+ C1 ∫idt −e(t ).
При ненулевых начальных условиях iL(0–) = iL(0), UC(0–) = UC(0) найдем изображение напряжения между узлами по Лапласу:
U |
|
|
|
=i RI (p), |
L di |
=i LpI (p)− Li |
(0), |
|||||
|
R i |
|
|
|
dt i |
|
L |
|
||||
UC (0 −)+ |
|
1 |
|
∫ |
idt i=i |
UC (0) |
+ |
I (p) |
, e(t ) i=i |
E (p), |
||
|
C |
|
|
|||||||||
|
|
|
|
p |
pC |
|
|
|||||
U (p)= RI (p)+ LpI (p)− LiL (0)+ UCp(0) + IpC(p) − E (p).
Отсюда следует, что
I (p)= U (p)+ LiL (0)(−U)Cp(0) + E (p), Z p
где Z (p)= R + Lp + pC1 – операторное сопротивление участка цепи.
Уравнение для изображения тока аналогично закону Ома в операторной форме для участка цепи, содержащего ЭДС, и ненулевых начальных условиях.
Слагаемое в числителе LiL(0) представляет собой внутреннюю ЭДС, обусловленную запасом энергии магнитного поля в индуктивности к момен-
ту коммутации. Слагаемое UCp(0) представляет собой внутреннюю ЭДС,
обусловленную запасом энергии электрического поля в конденсаторе к моменту коммутации. Заметим, что ЭДС LiL(0) направлена согласно с током, а
UC (0) – всегда навстречу току в ветви. p
Основы теории цепей. Конспект лекций |
-211- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Законы Ома и Кирхгофа в операторной форме
В соответствии с выражением для изображения тока можно построить схему замещения участка цепи (рис. 22.6).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I4(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UC (0) |
|
|
|
|||||||||
|
|
I1(p) |
|
|
|
R |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
pL |
|
Li(0) |
|
|
p |
|
|
|
pС |
|
|
E(p) |
|
|
t = 0 |
|||||
|
|
|
I(p) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I5(p) |
||
|
I3(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 22.6
Для участка цепи, не содержащего источника ЭДС при нулевых начальных условиях, запись закона Ома в операторной форме имеет более про-
стой вид: I(p) = U(p)/Z(p).
Первый закон Кирхгофа. Используя свойство линейности преобразования Лапласа, в общем случае можно сразу записать выражение первого закона Кирхгофа
∑I(p) = 0.
Второй закон Кирхгофа. Пусть имеем участок цепи (замкнутый контур на рис. 22.7). До коммутации i(0–) ≠ 0, UC(0–) ≠ 0.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t = 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
e1(t) |
|
|||||
|
|
|
|
R1 |
|
|
L |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
i1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i3 |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
e3(t) |
|||||||||
|
|
|
R3 |
|
|
C |
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 22.7
Выбрав направление обхода контура по часовой стрелке, запишем уравнение по второму закону Кирхгофа:
R1i1 + L didt1 + R3i3 + C1 ∫i3dt +UC (0)− R2i2 = e1 (t )−e3 (t ).
Заменив каждое из слагаемых изображением по Лапласу, получим
Основы теории цепей. Конспект лекций |
-212- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Законы Ома и Кирхгофа в операторной форме
R1I1 (p)+ LpI1 (p)− LiL (0)+ R3I3 (p)+ UCp(0) + I3 pC(p)1 − R2I2 (p)= E1 (t )− E3 (t ),
Z1 (p)I1 (p)− Z2 (p)I2 (p)+ Z3 (p)I3 (p)= E1 (t )− E3 (t )+ EВН (p),
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UC (0) |
|
|
Z |
(p)= R + Lp, |
Z |
|
(p)= R |
, |
Z |
|
(p) |
= R + |
|
1 |
, E |
|
( p) |
= Li |
L |
(0)− |
, |
|
|
|
|
pC |
|
p |
||||||||||||||
1 |
1 |
|
2 |
2 |
|
|
3 |
|
3 |
|
|
ВН |
|
|
|
|
|||
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
или в общем виде ∑Zk (p)Ik |
(p)= ∑Ek (p). |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
k=1 |
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, уравнение второго закона Кирхгофа в операторной форме содержит внутренние источники ЭДС, характеризующие энергетическое состояние цепи к моменту коммутации.
Последовательностьрасчетавоператорномметоде.
В общем случае порядок расчета переходных процессов операторным методом следующий:
1.Выбираются положительные направления токов в ветвях и записываются интегродифференциальные уравнения Кирхгофа для цепи после коммутации.
2.Записываются те же уравнения для изображений с учетом независимых начальных условий в виде внутренних источников ЭДС.
3.Полученные в операторной форме алгебраические уравнения решаются относительно изображения искомой величины.
4.Наосновеполученногоизображениянаходитсяоригиналискомойфункции.
Выше было показано, что законы Ома и Кирхгофа в операторной форме имеют запись, аналогичную записи в комплексной форме, и отличаются лишь введением внутренних ЭДС, учитывающих ненулевые начальные условия. Следовательно уравнения Кирхгофа для изображений могут быть составлены аналогично методу комплексных амплитуд, заменой в них jω на р и введением внутренних ЭДС.
Пример 3. Решить задачу, приведенную в примере 1, операторным методом. Схема цепи (рис. 21.1), параметры элементов и ЭДС даны там же.
Решение. 1. Очевидно, независимые начальные условия будут те же, что и в примере1:
iL(0–) = iL(0) = 1 A, UC(0–) = UC(0) = 40 B.
Основы теории цепей. Конспект лекций |
-213- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Последовательность расчета в операторном методе
С учетом внутренних источников ЭДС схема цепи приобретет вид, представленный на рис. 22.8.
|
|
|
|
|
R1 |
|
|
I1(p) |
|
|
|
|
|
|
|
R2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
I3(p) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2(p) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pL |
|
||||||
|
|
|
|
|
|
pС |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
UC (0) |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LiL(0) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 22.8
1. Системауравненийдляцепипослекоммутациитаже, что ивпримере1:
E = (R1 + R3 )i1 + C1 ∫i2dt,
1 di0 = −C ∫i2dt + R2i3 + L dt3 ,
0 = i1 −i2 −i3.
2. Эта система для изображений с учетом внутренних источников ЭДС имеет вид
E |
− |
UC (0) |
= |
(R |
+ R |
)I |
(p)+ |
1 |
I |
|
(p), |
||||||||||
|
|
|
|
|
2 |
||||||||||||||||
|
|
|
|
|
p |
|
1 |
|
|
3 |
|
1 |
|
|
pC |
|
|
||||
p |
|
(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
U |
C |
+ LiL |
(0)= − |
|
1 |
I2 |
(p)+(R2 |
+ pL)I3 (p), |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
p |
|
pC |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
= I |
(p)− I |
2 |
(p)− I |
3 |
(p). |
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Решим последнюю систему относительно изображения искомого тока:
Основы теории цепей. Конспект лекций |
-214- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Последовательность расчета в операторном методе
|
|
|
R |
+ R ) |
|
|
1 |
|
|
|
|
|
|
|
E |
− |
UC (0) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
3 |
|
pC |
|
|
|
|
|
p |
|
p |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
UC (0) |
(0) |
|
|
||||||||||
|
|
|
|
0 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
+ LiL |
|
|
|||||
|
|
|
|
|
pC |
|
|
|
|
|
p |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
−1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||
I3 (p)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
R + R ) |
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
3 |
|
|
|
|
|
pC |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
|
|
− |
1 |
|
|
R |
|
+ pL |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
pC |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
−1 |
|
|
−1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
60 10−3 p2 + 2410 p +106 |
= |
F1 |
(p) |
|
|
|
|
. |
||
p(60 10−3 p2 +1210 p +80 104 |
F2 |
(p) |
|||
4. Перейдем от изображения к оригиналу по теореме разложения
|
F |
(p) |
n |
F |
(p |
)epkt |
|
|
f (t ) i=i |
1 |
|
i=i ∑ |
1 |
k |
|
, |
|
F2 |
(p) |
F2′(pk ) |
||||||
|
k=1 |
|
||||||
где pk – корни F2(p), в нашем случае F2(p) имеет корни p = 0, p1 = –680, p2 = –19480.
F1(p) = 60·10-3p2 + 2410p + 106;
F2 (p)= p(60 10−3 p2 +1210 p +80 104;
F2′(p)= 3 60 10−3 p2 + 2 1210 p +80 104; p = 0 F1 (0)=106 , F2′(0)=80 104;
p1 = −680 |
F1 (p1 )= −62,04 104 , |
F2′(p1 )= −77 104; |
p2 = −19480 |
F1 (p2 )= −23,18 106 , |
F2′(p2 )= 21,96 106. |
Основы теории цепей. Конспект лекций |
-215- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Последовательность расчета в операторном методе
Таким образом,
i(t) = 1,25 + 0,805e–680t – 1,055e–19480t.
Пример 4. Операторным методом решить задачу, приведенную в примере 2, для гармонической ЭДС
e(t) = 100cos(ωt + 60º), где ω = 10000 рад/с.
Решение. Очевидно, независимые начальные условия будут те же, что и в примере 2:
iL(0–) = iL(0) = –0,03 A, UC(0–) = UC(0) = –1,42 B.
Эквивалентная схема цепи для изображений не зависит от вида ЭДС (рис. 22.8), следовательно, и система уравнений остается той же, что и в предыдущем примере:
E |
(p)− |
UC (0) |
= (R |
+ R )I |
(p) |
||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
p |
|
1 |
|
|
3 |
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
U |
C |
+ LiL |
( |
0)= − |
|
1 |
I |
|
(p)+ |
||||||||
|
|
|
|
|
|
|
|
2 |
|||||||||
|
|
p |
|
|
pC |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
= I |
(p)− I |
2 |
(p)− I |
3 |
(p). |
|
|
|||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ pC1 I2 (p),
(R2 + pL)I3 (p),
Однако изображение входной ЭДС в данном случае имеет вид
e(t )=100cos(ωt + 60°) i=i 100(p cosϕ−ωsin ϕ) = E (p).
p2 + ω2
Решив последнюю систему относительно изображения искомого тока, получим:
Основы теории цепей. Конспект лекций |
-216- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Последовательность расчета в операторном методе
|
|
|
R + R ) |
1 |
100 |
(p cosϕ−ωsin ϕ) |
− |
UC (0) |
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
1 |
3 |
|
pC |
|
|
p2 + ω2 |
|
|
p |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
0 |
− |
1 |
|
|
|
UC (0) + Li |
(0) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
pC |
|
|
|
|
p |
L |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
−1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||
I3 (p)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
R |
+ R ) |
1 |
|
|
0 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
3 |
|
pC |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
− |
1 |
R |
+ pL |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pC |
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
−1 |
|
−1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
−18 104 p3 −85,3 p2 +32,4 104 p −171 108 |
= |
F1 |
(p) |
|
|
|
|
. |
||
(p2 + ω2 )(60 10−3 p2 +1210 p +80 104 ) |
F2 |
(p) |
|||
Перейдем от изображения к оригиналу.
F2(p) имеет корни p1 = –680, p2 = –19480, p3,4 = ±j10000.
Согласно теореме разложения
|
|
|
|
|
F |
(p) |
n |
F |
(p |
)epkt |
|
|
|
|
|
f (t ) i=i |
1 |
|
i=i ∑ |
1 |
k |
|
. |
|
|
|
|
F2 |
(p) |
F2′(pk ) |
|||||
|
|
|
|
|
k=1 |
|
|||||
|
F |
(p )= −18 104 |
(−680)3 −85,3(−680)2 |
+32,4 104 (−680)−171 108 = |
|||||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= −174 108; |
|
|
|
|||
F |
(p |
2 |
)= −18 104 (−19480)3 −85,3(−19480)2 +32,4 104 (−19480)−171 108 = |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
= −424 108;
F1 (p3 )= −18 104 (j104 )3 −85,3(j104 )2 +32,4 104 (j104 )−171 108 =
=1010 e j150°;
Основы теории цепей. Конспект лекций |
-217- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Последовательность расчета в операторном методе
F1 (p4 )= −18 104 (− j104 )3 −85,3(− j104 )2 +32,4 104 (− j104 )−171 108 =
=1010 e− j150°;
F2 (p)= 60 10−3 p4 +1210 p3 + 680 104 p2 +1210 108 p +80 1012;
F2′(p)= 4 60 10−3 p3 +3 1210 p2 + 2 680 104 p +1210 108;
F2′(p1 )= 0,24(−680)3 +3630(−680)2 +1360(−680)+1210 108 =11,3 1010;
F2′(p2 )= 0,24(−19480)3 +3630(−19480)2 +1360(−19480)+1210 108 =
= −0,54 1012;
F2′(p3 )= 0,24(j104 )3 +3630(j104 )2 +1360(j104 )+1210 108 = 2,62 1011e j203°; F2′(p4 )= 0,24(− j104 )3 +3630(− j104 )2 +1360(− j104 )+1210 108 =
= 2,62 1011e j157°;
i |
|
(t )= |
1010 e j150° |
e j10000t + |
|
1010 e− j150° |
e− j10000t − 174 |
108 |
e−680t + |
|
3 |
|
2,62 1011e j 203° |
|
|
2,62 1011e j157° |
11,3 |
1010 |
|
||
|
|
|
|
|
|
|||||
|
|
−424 |
8 |
|
|
|
|
|
|
|
+ |
|
10 |
e−19480t = 0,038cos |
(10000t −53°)+ j0,038sin (10000t −53°)+ |
||||||
−0,54 |
12 |
|||||||||
|
10 |
|
|
|
|
|
|
|||
+0,038cos(10000t +307°)− j0,038sin (10000t +307°)−0,15e−680t + 0,79e−19480t = = 0,076cos(10000t −53°)−0,15e−680t + 0,79e−19480t .
Полученный результат совпадает с решением в примере 2.
Основы теории цепей. Конспект лекций |
-218- |

ЛЕКЦИЯ 22. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Контрольныевопросы
1.На чем основан операторный метод расчета переходных процессов?
2.Что называется преобразованием Лапласа?
3.Что такое оригинал и что такое изображение функции по Лапласу?
4.Каковы основные свойства преобразования Лапласа?
5.Какие методы перехода от изображения к оригиналу используются при расчете переходных процессов в простых цепях?
Основы теории цепей. Конспект лекций |
-219- |
