
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •ЛЕКЦИЯ 5. МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД
- •ЛЕКЦИЯ 7. МОЩНОСТЬ В ЦЕПИ ГАРМОНИЧЕСКОГО ТОКА
- •ЛЕКЦИЯ 8. ИЗБИРАТЕЛЬНЫЕ (РЕЗОНАНСНЫЕ) ЦЕПИ
- •ЛЕКЦИЯ 9. ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР
- •ЛЕКЦИЯ 10. СЛОЖНЫЕ СХЕМЫ ПАРАЛЛЕЛЬНЫХ КОНТУРОВ
- •ЛЕКЦИЯ 11. КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ. СВЯЗАННЫЕ КОНТУРЫ
- •ЛЕКЦИЯ 12. НАСТРОЙКА СВЯЗАННЫХ КОНТУРОВ
- •ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
- •ЛЕКЦИЯ 14. ОСНОВЫ ТЕОРИИ ЧЕТЫРЕХПОЛЮСНИКОВ
- •ЛЕКЦИЯ 15. ХАРАКТЕРИСТИЧЕСКИЕ (ВТОРИЧНЫЕ) ПАРАМЕТРЫ ЧЕТЫРЕХПОЛЮСНИКА
- •ЛЕКЦИЯ 17. СЛОЖНЫЕ ЧЕТЫРЕХПОЛЮСНИКИ
- •ЛЕКЦИЯ 18. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- •ЛЕКЦИЯ 20. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПИ RLC
- •ЛЕКЦИЯ 23. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ
- •ЛЕКЦИЯ 25. ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
- •ЛЕКЦИЯ 26. ФИЛЬТРЫ ВЕРХНИХ ЧАСТОТ
- •ЛЕКЦИЯ 27. ПОЛОСОВЫЕ ФИЛЬТРЫ
- •ЛЕКЦИЯ 28. ФИЛЬТРЫ ТИПА M
- •ЛЕКЦИЯ 29. БЕЗЫНДУКЦИОННЫЕ ФИЛЬТРЫ
- •ЛЕКЦИЯ 30. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- •ЛЕКЦИЯ 31. РЕЖИМ БЕГУЩИХ ВОЛН
- •ЛЕКЦИЯ 32. РЕЖИМ СТОЯЧИХ ВОЛН
- •ЛЕКЦИЯ 33. РЕЖИМ СМЕШАННЫХ ВОЛН
- •ЛЕКЦИЯ 34. СОГЛАСОВАНИЕ ЛИНИИ С НАГРУЗКОЙ
- •ЛЕКЦИЯ 35. ЧЕТВЕРТЬВОЛНОВЫЙ ТРАНСФОРМАТОР
- •ЛЕКЦИЯ 36. ВВЕДЕНИЕ В СИНТЕЗ ПАССИВНЫХ ЦЕПЕЙ
- •ЛЕКЦИЯ 37. СИНТЕЗ ДВУХПОЛЮСНИКОВ
- •ЛЕКЦИЯ 38. СВОЙСТВА И РЕАЛИЗАЦИЯ ВХОДНЫХ ФУНКЦИЙ RC-ДВУХПОЛЮСНИКОВ
- •ЛЕКЦИЯ 39. СИНТЕЗ RLC-ДВУХПОЛЮСНИКОВ
- •ЛЕКЦИЯ 40. СИНТЕЗ ЧЕТЫРЕХПОЛЮСНИКОВ
- •ЛЕКЦИЯ 41. ЛЕСТНИЧНЫЕ ЦЕПИ С ЭЛЕМЕНТАМИ ДВУХ ТИПОВ
- •ЛЕКЦИЯ 42. РЕАЛИЗАЦИЯ ЧЕТЫРЕХПОЛЮСНИКОВ МЕТОДОМ ДАРЛИНГТОНА
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
Полоса пропускания связанных контуров. Коэффициент передачи связанных контуров.
Основной интерес представляет поведение амплитуд токов в контурах вблизи резонансных частот системы. Для простоты полагаем, что резонансные частоты контуров равны между собой:
ω = ω = ω = |
|
1 |
|
= |
|
|
1 |
|
. |
||||||
|
|
|
|
|
|
|
|
||||||||
01 |
|
02 |
0 |
|
|
L11C11 |
|
L22C22 |
|||||||
|
|
|
|
|
|
|
|||||||||
Полные сопротивления контуров |
|
|
|
|
|
|
|
|
|
||||||
Z |
= R |
+ jX |
11 |
= R |
1+ j |
|
X11 |
, |
|||||||
|
|
|
|||||||||||||
|
11 |
1 |
|
1 |
|
|
R1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
Z |
22 |
= R |
+ jX |
22 |
= R |
1+ j |
|
X22 |
. |
||||||
|
|
||||||||||||||
|
2 |
|
2 |
|
R2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
На частотах близких к резонансной частоте |
|
|
|||||||||
Δω |
|
X |
|
ω |
|
ω |
|
|
2(ω−ω0 ) |
|
|
|
1, |
|
= ξ = Q |
|
− |
0 |
|
≈ |
|
Q |
|
ω0 |
R |
ω0 |
ω0 |
||||||||
|
|
|
ω |
|
|
|
|||||
и
Z11 = R1 + jX11 ≈ R1 (1+ jξ1 ),
Z22 = R2 + jX22 ≈ R2 (1+ jξ2 ),
где ξ1, ξ2 – обобщенная расстройка первого и второго контуров. Ток в первом контуре
I1 = |
|
|
|
|
E |
|
= |
|
|
|
|
|
E |
|
|
|
|
|
= |
||||
Z |
+ |
|
X122 |
|
|
R |
(1+ jξ )+ |
|
|
X122 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
(1+ jξ2 ) |
|
|
||||||||||||||||
|
|
11 |
|
|
|
Z22 |
|
|
|
|
1 |
1 |
|
R2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
E |
|
|
|
|
|
|
|
|
|
(1+ jξ2 ) |
|
|
|
|
|
. |
|
|
|||
|
R |
|
|
|
|
|
|
|
|
X 2 |
|
|
|
|
|
|
|
||||||
|
|
|
1 1−ξ ξ |
+ |
|
12 |
+ j ( |
ξ + ξ |
2 |
) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
R1R2 |
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Основы теории цепей. Конспект лекций |
-111- |
ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
Ток во втором контуре
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
± j |
|
X12 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
E |
|
|
|
± jX |
|
|
E |
|
|
|
|
|
|
|
R R |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
I |
2 |
= |
|
|
|
|
|
|
12 |
= |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
. |
|
|
|
||||
Z + |
X 2 |
|
Z |
|
R R |
|
|
|
|
|
X 2 |
|
|
+ j (ξ +ξ |
|
) |
|
|
|
|||||||||||||||||||
|
|
|
|
22 |
|
|
|
1−ξ ξ |
|
+ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
12 |
|
|
|
|
1 2 |
|
|
2 |
|
|
12 |
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
11 |
Z22 |
|
|
|
|
|
|
|
|
|
1 |
|
|
R1R2 |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
2 |
|
|
|
|
|
X 2 |
|
ρ ρ |
2 |
|
|
|
||||||
На частотах, близких к резонансной частоте, |
|
12 |
|
= |
12 |
|
1 |
2 |
= k |
Q Q . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1R2 |
|
|
ρ1ρ2 R1R2 |
|
|
1 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Кроме того, выше было получено |
|
|
E |
= 2I |
2mm |
, |
|
|
|
E |
= 2I |
|
|
|
(X12opt ) |
. |
|
|||||||||||||||||||||
|
|
R1R2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
1max |
|
|
||||||||||||
Таким образом, подставив последние выражения в формулы для токов, получим уравнения нормированных резонансных кривых первого и второго контуров
n = |
|
|
I1 |
|
|
= |
|
|
2 1+ ξ22 |
|
|
|
|
e− j(ϕ12 −ϕ2 ), |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
I1max(X12opt ) |
|
(1−ξ1ξ2 + k2Q1Q2 )2 +(ξ1 + ξ2 )2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||
n = I2 = |
|
|
|
|
2k Q1Q2 |
|
− j |
|
ϕ ± |
π |
|
|
||||||
|
|
|
|
|
e |
|
12 |
2 , |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2mm |
|
(1−ξ1ξ2 + k2Q1Q2 )2 +(ξ1 + ξ2 )2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
где ϕ12 = arctg |
|
|
ξ1 + ξ2 |
|
|
, ϕ2 = arctg ξ2 , ± |
π |
− фаза |
X12 , + |
π |
– соот- |
|||||||
1−ξ ξ |
2 |
+ k2Q Q |
2 |
2 |
||||||||||||||
|
|
1 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|||
ветствует емкостной связи, − π2 – магнитной связи.
Для одинаковых контуров, использующихся в полосовых фильтрах приемников:
Q1 = Q2 = Q, ξ1 = ξ2 = ξ;
амплитудно-частотные характеристики первого и второго контуров
n1 |
= |
|
2 1 |
+ ξ2 |
|
, n2 = |
|
|
2kQ |
|
|
; |
|
( |
|
|
) |
|
( |
|
|
) |
|
||||
|
|
−ξ2 + k |
2Q2 |
2 + 4ξ2 |
−ξ2 |
+ k2Q2 |
2 + 4ξ2 |
||||||
|
|
1 |
|
1 |
|
||||||||
фазочастотные характеристики первого и второго контуров
Основы теории цепей. Конспект лекций |
-112- |
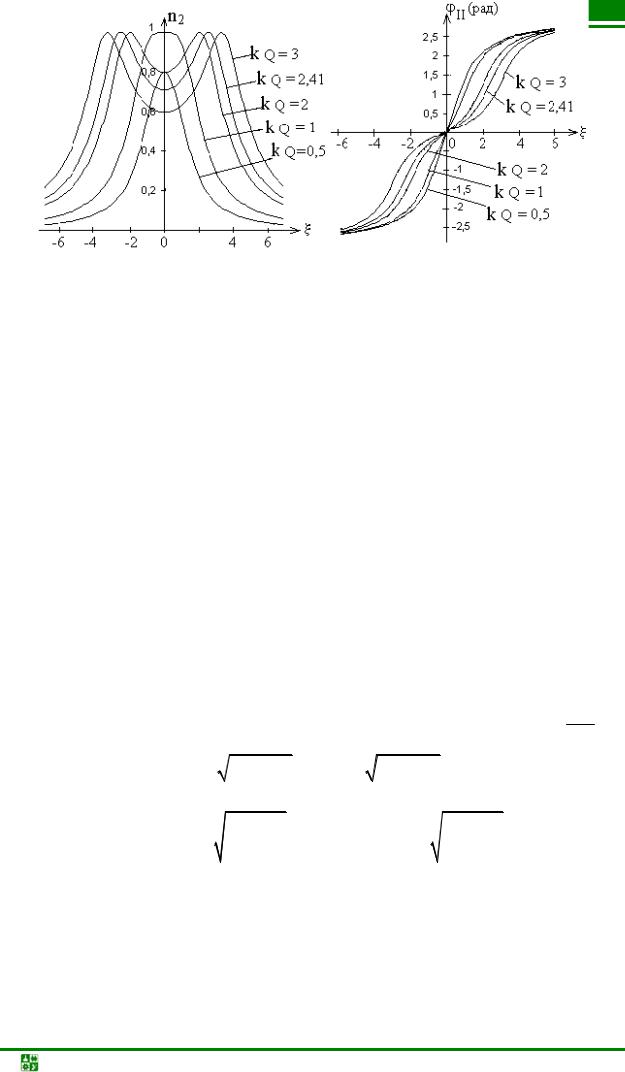
ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
ϕ1 = arctg1−ξ22+ξk 2Q2 −arctg ξ, ϕ2 = arctg1−ξ22+ξk2Q2 ± π2 .
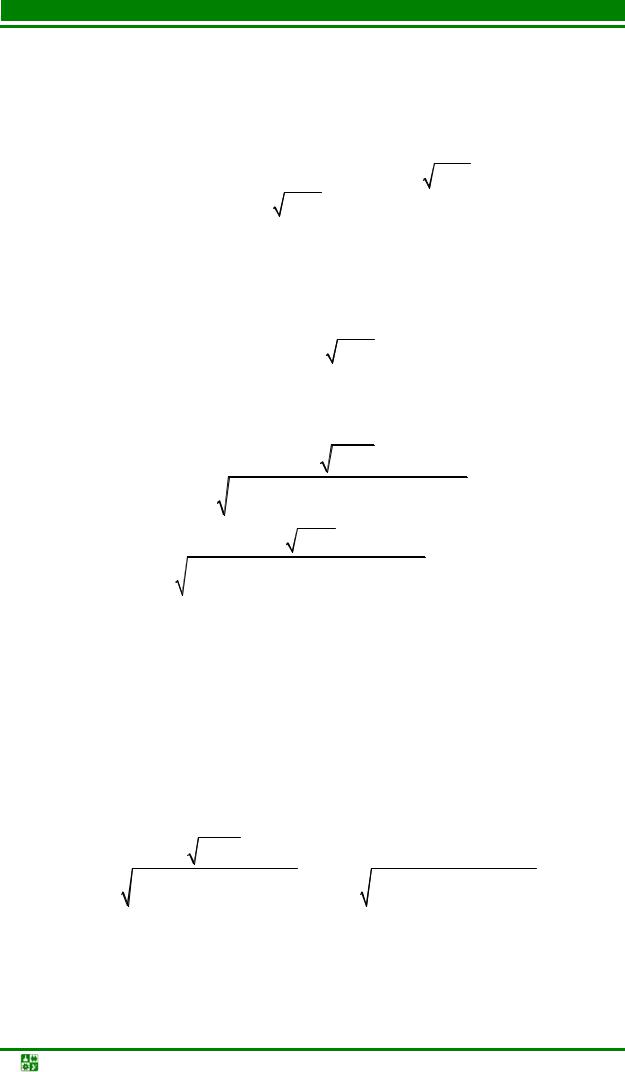
На рис. 13.1 приведены АЧХ и ФЧХ второго контура в функции обобщенной расстройки при пяти различных значениях произведения kQ. (kQ характеризует степень связи контуров и называется параметром или фактором связи.)
n2
kQ = 3 kQ = 2,41 kQ = 2
kQ = 1 kQ = 0,5
φ2, рад
kQ = 3 kQ = 2,41
kQ = 2 kQ = 1 kQ = 0,5
а |
б |
Рис. 13.1
Из графиков амплитудно-частотной характеристики (рис. 13.1, а) видно, что при факторе связи kQ < 1 кривые имеют одногорбый характер с максимумом на резонансной частоте (ξ = 0, ω = ω0). При kQ = 1 кривая АЧХ является предельной одногорбой кривой, коэффициент связи kKP = 1/Q называется критическим. При факторе связи kQ > 1 кривые имеют два максимума на частотах ниже и выше резонансной частоты контуров и минимум на резонансной частоте. Частоты максимумов (частоты связи) можно определить из
условия равенства нулю производной АЧХ по обобщенной расстройке dndξ2 = 0
|
|
|
ξ = k 2Q2 −1, ξ = − k2Q2 |
−1 , |
|
|
|
|
||||||||||||
откуда |
|
|
1 |
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
k |
2 |
|
1 |
|
|
|
|
|
|
1 |
k |
2 |
|
1 |
|
ω1 |
= ω0 |
1 |
− |
|
|
− |
|
|
, |
ω11 |
= ω0 |
1 |
+ |
|
|
− |
|
. |
||
2 |
|
Q2 |
2 |
|
Q2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Фазочастотная характеристика (рис. 13.1, б), построенная для соответствующих факторов связи, должна быть поднята по оси ординат на π/2 при емкостной связи и опущена также на π/2 при индуктивной связи.
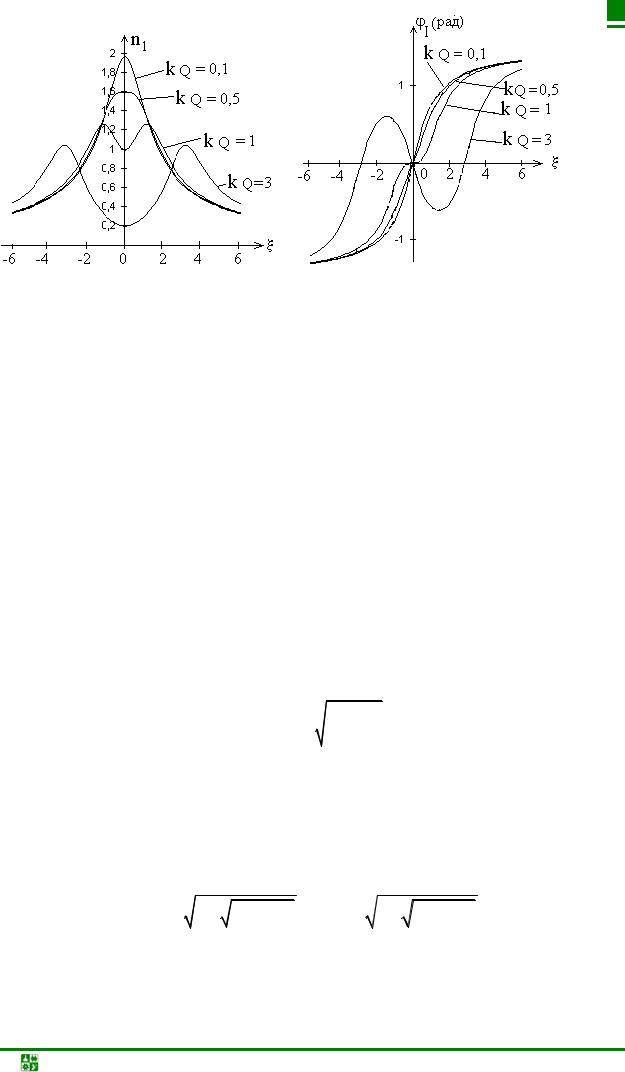
Частотные характеристики первого контура (рис. 13.2) изменяются более резко при изменении обобщенной расстройки, чем характеристики второ-
Основы теории цепей. Конспект лекций |
-113- |
ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
го контура. Это объясняется наличием в выражении для резонансной кривой в числителе множителя, зависящего от величины расстройки (в аналогичном выражении для второго контура числитель от частоты не зависит).
|
|
|
|
|
|
|
|
|
|
φ1, рад |
|
|||||||
n1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kQ = 0,1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
kQ = 0,1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kQ = 0,5 |
|||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
kQ = 0,5 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kQ = 1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kQ = 1 |
kQ = 3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kQ = 3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
Рис. 13.2
Таким образом, образование седловины на АЧХ первого контура получается при меньших факторах связи, чем во втором контуре (рис. 13.2, а). Фазочастотная характеристика (рис. 13.2, б) при факторах связи больше единицы трижды переходит через нуль, что соответствует резонансной частоте (ξ = 0) и частотам связи.
Если два связанных контура имеют одинаковые резонансные частоты, но разные добротности (Q1 > Q2, что характерно для выходных каскадов передатчиков, нагруженных на сопротивление нагрузки), то условием образования седловины на кривой тока второго контура является
|
|
|
|
|
|
k > kKP = |
d1 + d2 |
, |
|
|
|
|
|
|
|
2 |
|
где d = |
1 |
и d |
2 |
= |
1 |
– затухание контуров. |
|
|
|
|
|
||||||
1 |
Q1 |
|
|
Q2 |
|
|
|
|
|
|
|
|
|
|
|
||
При этом частоты связи тем больше отличаются от резонансной частоты, чем больше коэффициент связи отличается от критического
ω1 = |
ω0 |
, |
ω11 = |
ω0 |
. |
|
1+ k2 − kKP2 |
1− k2 − kKP2 |
|||||
|
|
|
|
Основы теории цепей. Конспект лекций |
-114- |
ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
Полосапропусканиясвязанныхконтуров.
Полосой пропускания системы связанных контуров называют полосу
12 от наибольшего его значения при заданных параметрах контуров и коэффициенте связи. Так как резонансные кривые тока второго контура зависят от фактора связи kQ, то следует рассмотреть три случая: kQ < 1, kQ = 1 и kQ > 1.
1.Связь слабая kQ < 1. Если контуры одинаковы Q1 = Q2 = Q и ω01 = ω02 =
=ω0, то в этом случае кривая тока второго контура является одногорбой и
имеет максимум на резонансной частоте |
n |
(0)= |
|
|
2kQ |
. |
|
|||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
+ k2Q2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Обобщенная расстройка на границах полосы пропускания определяется |
||||||||||||||||||||||
из выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 (0) |
= |
|
2kQ |
= |
|
|
2kQ |
, |
|||||||||||||
|
2 |
|
|
|
|
2 (1+ k2Q2 ) |
|
(1−ξ02 + k2Q2 )2 + 4ξ02 |
||||||||||||||
откуда получается |
|
ξ0 |
|
|
= |
k 2Q2 −1+ |
2(1+ k4Q4 ). |
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||||||
При kQ 1, |
|
ξ0 |
|
= |
−1+ 2 ≈ |
0,41 ≈ 0,64 |
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||||||||
2Δω = ξ0 ω0 |
= 0,64 2Δω, т. е. полоса пропускания 2∆ωCB связанных |
|||||||||||||||||||||
CB |
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
контуров составляет 0,64 от полосы пропускания 2∆ω одиночного контура. 2. При критической связи kQ = 1
ξ0 = 1−1+ 2(1+1) = 2, т. е. 2ΔωCB = 2 2Δω.
3. При сильной связи kQ > 1 обобщенную расстройку на границах полосы пропускания следует определять из общего выражения
1 |
= |
2kQ |
|
, |
2 |
(1−ξ02 + k2Q2 )2 |
|
||
|
+ 4ξ02 |
|||
откуда получается ξ0 = k2Q2 + 2kQ −1 .
Очевидно, что с ростом фактора связи увеличивается и обобщенная расстройка. Можно показать, что при kQ > 2,41 на резонансной частоте воз-
Основы теории цепей. Конспект лекций |
-115- |

ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
Полоса пропускания связанных контуров
никает впадина на частотной характеристике ниже уровня |
1 |
от максимума |
|
2 |
|||
|
|
и условия для полосы пропускания перестают выполняться. Появляется две полосы пропускания, разделенные по частоте тем дальше, чем больше фактор связи превышает величину 2,41.
В предельном случае kQ = 2,41,
2∆ωCB = 3,1·2∆ω,
т. е. полоса пропускания в 3,1 раза шире полосы одиночного контура.
На рис. 13.3 приведена зависимость полосы пропускания связанных контуров от фактора связи kQ.
–полоса пропускания связанных контуров
–полоса пропускания одиночного контура
kQ
Рис. 13.3
Таким образом, при слабой связи (kQ << 1) полоса пропускания связанных контуров составляет примерно 0,64 от полосы одиночного контура. С увеличением фактора связи полоса пропускания возрастает (при kQ = 1 полоса пропускания системы равна 1,41 от полосы одиночного контура). Дальнейшее увеличение kQ приводит к появлению двугорбой кривой тока второго контура, при kQ = 2,41 впадина на резонансной частоте становится равной
12 от максимума тока и полоса пропускания достигает максимальной шири-
ны, равной 3,1 от полосы одиночного контура. При kQ >> 2,41 полоса пропускания разрывается на две части, так как впадина в точке, соответствующей ξ = 0, становится ниже, чем определяется условием полосы пропускания.
Коэффициентпередачисвязанныхконтуров.
Часто на практике необходимо знать, как зависит напряжение на реактивных элементах второго контура при изменении частоты источника сигнала. Для этой цели вводится комплексный коэффициент передачи по напряжению
Основы теории цепей. Конспект лекций |
-116- |
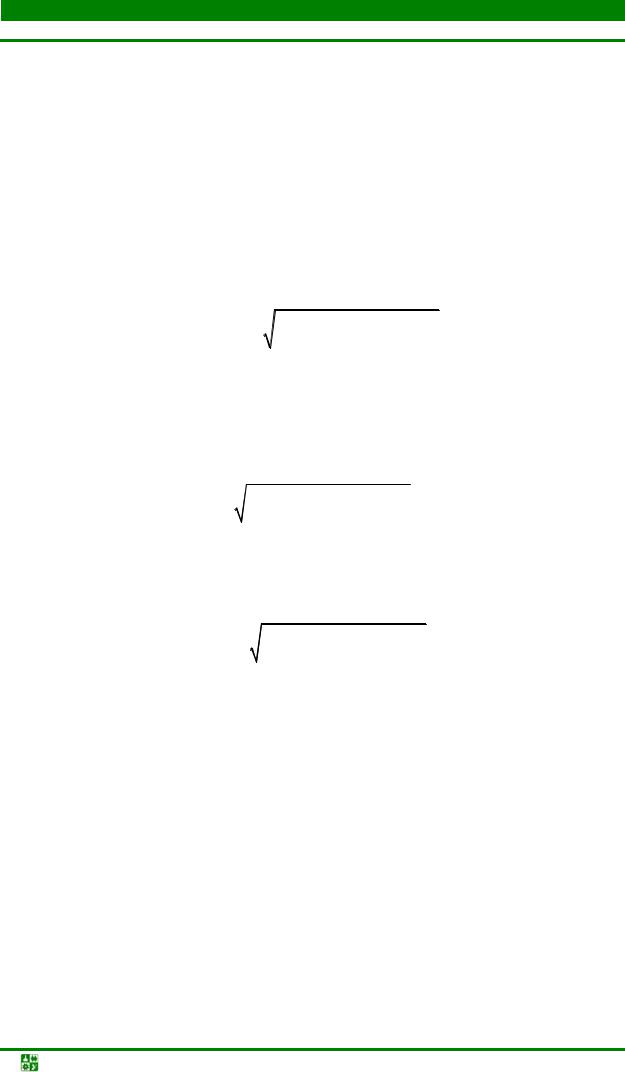
ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
Коэффициент передачи связанных контуров
|
|
|
|
|
|
|
|
|
|
K = |
U2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где U |
|
= I |
|
1 |
, если напряжение снимается с емкости и U |
|
= I |
|
jωL , если |
|||||||||||||||||||
|
|
jωC2 |
|
|
||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
|
напряжение снимается с индуктивности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Амплитуда тока второго контура |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
I |
2 |
= n I |
2mm |
= |
|
|
|
2kQ |
|
|
|
|
|
|
E |
, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
( |
2 |
+ k |
2 |
Q |
2 |
) |
2 |
|
2 |
|
2R |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1−ξ |
|
+ 4ξ |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
тогда модуль комплексного коэффициента передачи, если напряжение снимается с емкости
|
|
|
|
I2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
K |
|
= |
ωC |
2 |
|
|
= |
|
|
|
|
|
|
2kQ |
|
|
|
|
|
|
|
|
|
|
E |
|
1 |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
E |
|
|
|
|
|
|
( |
|
2 |
|
|
2 |
Q |
2 |
) |
2 |
|
|
|
2 2R |
|
ωC2E |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
−ξ |
|
|
|
+ |
4ξ |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ k |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
При малых расстройках |
|
|
|
1 |
|
|
= Q , следовательно, |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
RωC2 |
|
|
|
|
kQ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
K |
|
= Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
( |
|
|
2 |
|
2 |
Q |
2 |
) |
2 |
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−ξ |
|
|
+ 4ξ |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ k |
|
|
|
|
|
|
|
|
|
|
|||||||||
Таким образом, коэффициент передачи по напряжению имеет характер частотной зависимости, аналогичный зависимости тока второго контура. Если фактор связи kQ < 1, то кривая коэффициента передачи одногорбая, если kQ > 1, то двугорбая. При критической связи (kQ = 1) на резонансной частоте |K| = Q/2, т. е. чем больше добротность контуров системы, тем больше напряжение на выходе.
Очевидно, что кривые зависимости фазы комплексного коэффициента передачи от частоты совпадают с кривыми ФЧХ второго контура, если их опустить на π/2 при съеме напряжения с емкости (напряжение на емкости отстает от тока на π/2) и поднять на π/2 при съеме напряжения с индуктивности (напряжение на индуктивности опережает ток на π/2).
Основы теории цепей. Конспект лекций |
-117- |
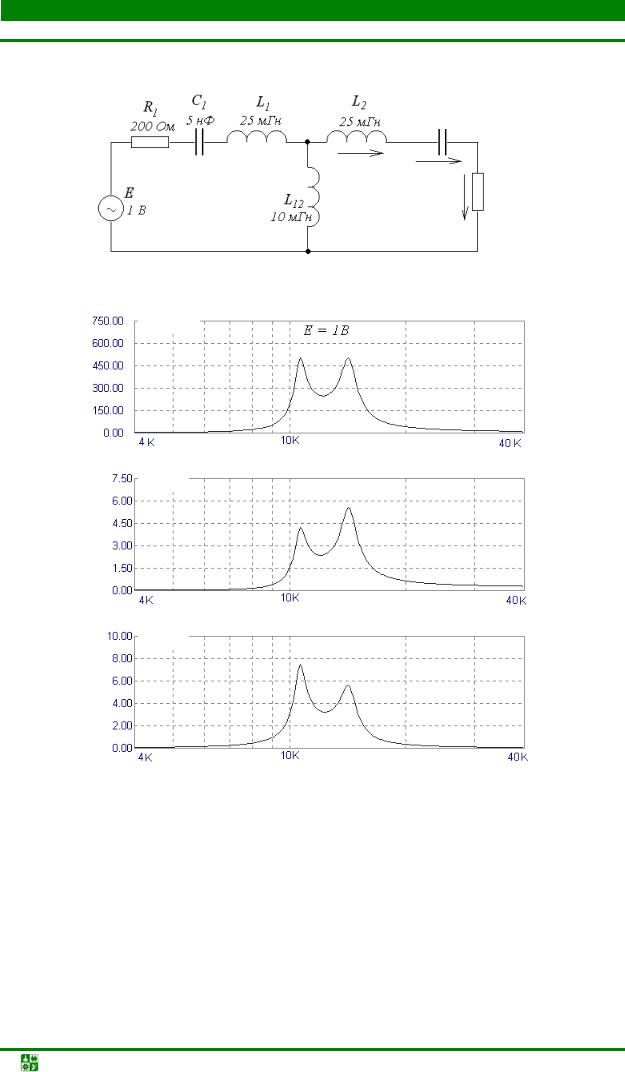
ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
Коэффициент передачи связанных контуров
|
|
С1 |
|
L1 |
|
L2 |
R1 |
|
|||||
|
5 нФ |
|
25 мГн |
|
25 мГн |
|
200 Ом |
|
|
|
|||
|
|
|
|
|
|
UL2
Е |
|
|
|
L12 |
|||
1 В |
|
||
|
10 мГн |
||
|
|
Рис. 13.4
UR2, мВ
а
UL2, В
б
UC2, В
в
Рис. 13.5
С2 |
|
|
5 нФ |
|
|
UC2 |
R2 |
|
UR2 |
||
200 Ом |
F
F
F
Следует отметить, что хотя у одинаковых контуров (рис. 13.4) при kQ > 1 амплитуды токов на частотах связи одинаковы (рис. 13.5, а), амплитуды напряжений на индуктивности и емкости (рис. 13.5, б, в) различны, поскольку
U |
C 2 |
= I |
|
1 |
, U |
L2 |
= I |
ωL , |
ω < ω . |
|
|
||||||||
|
|
2 ωC2 |
2 |
2 |
1 11 |
||||
Основы теории цепей. Конспект лекций |
-118- |

ЛЕКЦИЯ 13. РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ
Контрольныевопросы
1.Что такое амплитудно-частотные характеристики контуров?
2.Что такое фазочастотные характеристики контуров?
3.Что такое параметр или фактор связи?
4.Что называют полосой пропускания системы связанных контуров?
5.Чем определяется коэффициент передачи связанных контуров?
Основы теории цепей. Конспект лекций |
-119- |
