3.3. Перетворення компонент тензора деформації при заміні системи відліку

Оскільки деформація пружного тіла розглядається в околі точки, з якою зв’язана відповідна система координат, то компоненти тензора деформації при поворотах без зміни центра будуть змінюватися.

Розглянемо систему координат з базисними векторами . Нехай базисні вектори нової системи з тим же центром.

Напрямні косинуси векторів , , у старій системі координат наведені у табл. 3.1.

Таблиця 3.1

	l1	m1	n1
	l2	m2	n2
	l3	m1	n3

На підставі цієї таблиці формули переходу від величин до запишуться у вигляді

;

;

. (3.28)

Так як величина є інваріантом при перетворенні (3.28), то має місце рівність

, (3.29)

де – компоненти тензора деформації в новій системі координат.

Підставляючи (3.28) в середню частину формули (3.29), одержимо

. (3.30)

Порівнюючи в (3.30) коефіцієнти при однакових , знаходимо формули переходу від до .

;

;

; (3.31)

;

;

.

Обернене перетворення можна одержати, розв’язавши (3.31) відносно .

3.4. Головні напрямки тензора деформації. Головні осі і головні деформації

Розглянемо задачу зведення матриці тензора деформації до канонічного вигляду. Це означає, що певним вибором системи координат можна добитися того, щоб ця матриця стала діагональною.

Така задача еквівалентна задачі знаходження власних чисел і власних векторів матриці

. (3.32)

Для того, щоб визначити власні числа матриці (3.13) тензора деформації, складаємо характеристичне рівняння

. (3.33)

Розкриваючи ліву частину, знаходимо

(3.34)

або

. (3.35)

Тут введено позначення

;

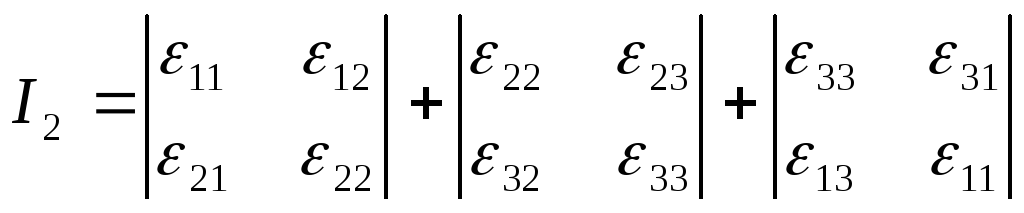, (3.36)

– визначник матриці тензора деформації.

Можна показати, що величини , , інваріантні при повороті системи відліку. Це означає, що коефіцієнти характеристичного рівняння однакові в різних системах координат.

Розв’язок характеристичного рівняння , , визначає діагональні елементи матриці тензора деформації в новій системі координат. Позначимо ці елементи через

; ; . (3.37)

Можна довести, що характеристичне рівняння (3.35) має тільки дійсні корені.

Для знаходження власних векторів , які визначають напрямки нових координатних осей, складаємо систему рівнянь (3.32)

, . (3.38)

Ця система однорідна з нульовим визначником, тому відношення визначаються однозначно. Якщо координатні осі нової системи координат напрямити по векторах , то матриця тензора деформації прийме вигляд

.

У цьому випадку деформацію в точці пружного тіла можна розглядати як розтяг (стиск) в трьох взаємноперпендикулярних напрямках.

Напрямки називаються головними напрямками тензора деформації, а відповідні їм координатні осі – головними осями тензора деформації. Деформації , , називаються головними деформаціями.

Вияснимо геометричний зміст інваріанта .Виберемо в околі точки елементарний паралелепіпед із сторонами , , , які мають напрямки головних осей тензора деформації . Його об’єм . Внаслідок деформації елемент також буде прямокутним паралелепіпедом, об’єм якого

. (3.39)

Визначимо відносну зміну об’єму внаслідок деформації (добутками головних деформацій нехтуємо)

. (3.40)

Враховуючи, що , із (3.40) знаходимо

. (3.41)

Прийнявши до уваги диференціальні залежності Коші (3.15), одержимо

. (3.42)