6.7. Принцип Сен-Венана

Суттєві математичні труднощі при розв’язуванні прямої задачі виникають внаслідок необхідності задоволення конкретним її граничним умовам. Разом з тим із міркувань фізичного характеру зрозуміло, що точне здійснення розподілу поверхневих сил, на окремих ділянках поверхні тіла, на яких цей розподіл вважається заданим, як певні граничні умови, практично навряд чи здійснимий. У багатьох задачах поверхневі сили, які прикладені до ділянок поверхні тіла відомі тільки сумарно, тобто як їх головний вектор і головний момент, а закон розподілу поверхневих сил відомий приблизно або зовсім невідомий. Таким чином, поряд з математичними труднощами, з якими доводиться зустрічатися при розв’язуванні граничних задач теорії пружності, мають місце труднощі при точному формулюванні граничних умов. Ці труднощі значно зменшуються завдяки так званому принципу Сен-Венана: якщо до малої ділянки поверхні тіла прикладена зрівноважена система сил (головний вектор і головний момент дорівнюють нулю), то ця система сил викликає локальний напружено-деформований стан, який швидко зникає при віддаленні від ділянки прикладання сил.

Принцип Сен-Венана можна сформулювати в іншому варіанті: якщо деяку сукупність поверхневих сил на порівняно малій частині поверхні тіла замінити статично еквівалентною системою сил, що діють на тій же частині поверхні, то така заміна сил практично не змінює напружень і зміщень у точках, які віддалені від площадки прикладання сил на відстань, яка не менша ніж найбільший лінійний розмір цієї площадки.

Принцип Сен-Венана дозволяє задовольняти граничним умовам інтегрально, тобто задовольняти не конкретному закону розподілу поверхневих сил, а їх головному вектору і головному моменту. Принцип Сен-Венана досить добре підтверджується експериментально.

8. Найпростіші задачі теорії пружності

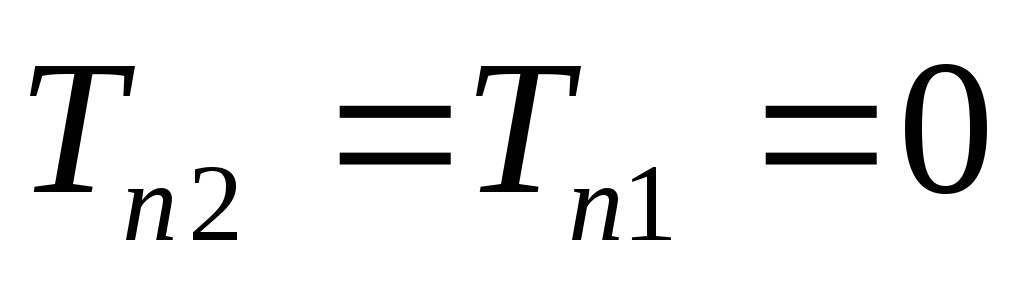1. Розтяг призматичного бруса. Розглянемо призматичний брус (рис. 6.1), довжина якого значно більша від лінійного розміру сталого поперечного перерізу довільної форми. Початок координат сумістимо з центром ваги лівого торця бруса, а вісь напрямимо вздовж осі бруса. Бічна поверхня бруса вільна від поверхневих сил, а до торців прикладені рівномірно розподілені поверхневі сили (), які розтягують брус рівнодійними силами , де – площа поперечного перерізу. Масовими силами нехтуємо.

Розв’язуючи задачу напівоберненим методом Сен-Венана, приймаємо, що в довільний точці бруса

, , (6.35)

де , – сталі, які підлягають визначенню.

Рис. 6.1

Компоненти тензора напружень (6.35) тотожно задовольняють рівнянням Бельтрамі-Мічелла (6.33) як лінійні функції і двом першим рівнянням рівноваги (6.3). Третє рівняння (6.3) буде виконуватися при

, тобто коли . (6.36)

Розглянемо граничні умови (6.6)

. (6.37)

Для довільної точки бічної поверхні бруса , тому умови (6.37) виконуються при довільному значенні . Для точок лівого і правого торців , , тому на торцях перші дві граничні умови виконуються тотожно, а з третьої визначаємо

. (6.38)

За законом Гука (6.5) одержимо

; ; . (6.39)

Будемо вважати, що окіл точки, яка співпадає з початком координат 0, не має зміщення, тобто при

; . (6.40)

Використовуючи залежність , із (6.39) знаходимо

; . (6.41)

Решту компонент () визначаємо за формулою (3.62)

, (6.42)

з якої знаходимо

. (6.43)

Компоненти вектора зміщення через компоненти відносного зміщення визначаються за формулою (3.64), яка в даному випадку приймає вигляд

. (6.44)

Підставляючи (6.41), (6.43) в (6.44), знаходимо

; ; . (6.45)

Із останнього співвідношення (6.45) випливає, що поперечні перерізи бруса залишаються плоскими, що підтверджує відому з курсу опору матеріалів гіпотезу плоских перерізів. Повне видовження бруса визначається за формулою

. (6.46)

Таким чином, одержані із основних рівнянь теорії пружності результати, співпадають з розв’язком, відомим із курсу опору матеріалів. Однак цей розв’язок буде точним при умові, що сили, які розтягують брус, розподілені по його торцях рівномірно. Але згідно з принципом Сен-Венана цей розв’язок можна вважати точним і при іншому способі прикладання розтягуючих сил.

2. Розтяг призматичного бруса під дією власної ваги. Вертикально розміщений призматичний брус сталого поперечного перерізу довжиною закріплений на верхньому торці й перебуває під дією власної ваги. Початок системи координат сумістимо з центром ваги нижнього торця недеформованого бруса, направивши вісь 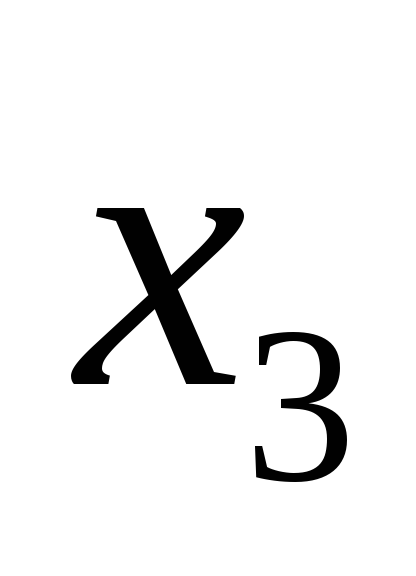вгору вздовж осі бруса.

На брус діють тільки об’ємні сили

, (6.47)

і реактивні поверхневі сили на верхньому закріпленому торці, які сумарно дорівнюють вазі бруса , де – площа поперечного перерізу бруса.

Диференціальні рівняння рівноваги (6.3) і умови сумісності Бельтрамі-Мічелла (6.32) будуть виконуватися, якщо в довільній точці прийняти

, . (6.48)

Граничні умови (6.6) на бічній поверхні бруса і на його нижньому торці (; ), які вільні від зовнішніх поверхневих сил, виконуються тотожно. На верхньому торці (; ) гранична умова приймає вигляд

, (6.49)

тобто розв’язок буде точним для даної задачі, якщо зрівноважуючі вагу бруса поверхневі сили на закріпленому верхньому торці розподілені рівномірно. Згідно з принципом Сен-Венана, цей розв’язок буде добрим наближенням і при іншому способі розподілу реактивних поверхневих сил з рівнодійною , яка напрямлена вздовж осі . За законом Гука (6.4) визначаємо

; ; . (6.50)

Закріплення верхнього торця приймемо таким, при якому окіл точки , яка співпадає з центром ваги торця, не має зміщення і повороту, тобто при ,

; . (6.51)

За формулами (6.5), (6.42), суміщуючи початок ламаної інтегрування з точкою , знаходимо

; ;

; ; ; (6.52)

; ; .

Виконуючи інтегрування від точки за формулою (6.44), одержимо

; ; . (6.53)

З формул (6.53) випливає, що точки осі мають тільки вертикальні зміщення

.

При цьому поперечні перерізи бруса внаслідок деформації викривляються і приймають форму параболоїда обертання.