
- •Механіка суцільного середовища
- •Кінематика суцільного середовища
- •Основні поняття і задачі механіки суцільного середовища
- •Способи задання руху суцільного середовища
- •Розділ 2 елементи гідродинаміки
- •2.1. Основні поняття і формули векторного аналізу
- •2.2. Рівняння неперервності руху ідеальної рідини
- •2.3. Рівняння Ейлера
- •2.4. Гідростатика
- •2.5. Умова відсутності конвекції
- •2.6. Рівняння Бернуллі
- •Основи теорії пружності (теорія деформації)
- •3.1. Вектор зміщення і деформований стан
- •3.2. Тензор деформації
- •3.3. Перетворення компонент тензора деформації при заміні системи відліку
- •3.4. Головні напрямки тензора деформації. Головні осі і головні деформації
- •3.5. Визначення компонент вектора зміщення через компоненти тензора деформації
- •3.6. Визначення зміщень через компоненти тензора відносного зміщення
- •Основи теорії пружності (теорія напружень)
- •4.1 Зовнішні сили. Вектор напруження. Напружений стан тіла
- •4.2. Тензор напружень
- •4.3. Диференціальні рівняння рівноваги пружного тіла. Симетричність тензора напружень
- •4.4. Перетворення компонент тензора напружень при повороті системи координат
- •4.5. Головні напруження і інваріанти тензора напружень
- •Основи теорії пружності (співвідношення між компонентами тензора напружень)
- •5.1. Узагальнений закон Гука
- •Основи теорії пружності (основні рівняння і задачі теорії пружності)
- •6.1. Основні рівняння теорії пружності
- •6.2. Основні задачі статики пружного тіла
- •6.3. Пряма і обернена задачі теорії пружності
- •6.4. Рівняння пружної рівноваги в зміщеннях
- •6.5. Основні рівняння в напруженнях
- •Застосовуючи до (6.32) оператор Лапласа, одержимо
- •6.6. Напівобернений метод Сен-Венана
- •6.7. Принцип Сен-Венана
- •Найпростіші задачі теорії пружності
- •Метод суперпозиції
- •Основи теорії пружності (плоска задача теорії пружності)
- •7.1. Плоска деформація
- •7.2. Плоский напружений стан
- •7.3. Узагальнений плоский напружений стан
- •7.4. Основні рівняння плоскої теорії пружності. Зведення до бігармонічної проблеми
- •7.5. Плоска задача в декартових координатах
- •Нехай функція напружень має вигляд полінома третього степеня
- •Виберемо функцію напружень у вигляді полінома четвертого степеня
- •Якщо розглядається друга гранична задача, то граничні умови мають вигляд
- •8.2. Зведення основної задачі до бігармонічної проблеми
- •8.3. Задачі, в яких напруження залежать тільки від
- •Задачі, в яких напруження залежать від і
- •Підставляючи (8.67) у (8.64), одержимо формули для напружень
- •Застосування функцій комплексної змінної до розв’язування задач плоскої теорії пружності
- •9.1. Комплексне подання функції напружень
- •Розглянемо основне рівняння плоскої теорії пружності
- •9.2. Комплексне подання компонент тензора напружень і вектора зміщень
- •9.3. Степінь визначеності і структура комплексних потенціалів
- •9.4. Перетворення рівнянь плоскої задачі теорії пружності при конформному відображенні
- •9.5. Двосторонній розтяг нескінченної площини з еліптичним отвором
- •Список літератури
9.5. Двосторонній розтяг нескінченної площини з еліптичним отвором
Нехай
гладкий замкнутий контур
![]() ,
точки якого позначимо через
,
точки якого позначимо через
![]() ,
ділить площину
,
ділить площину
![]() на внутрішню скінчену область
на внутрішню скінчену область
![]() ,
яка залишається зліва при обході
,
яка залишається зліва при обході
![]() проти годинникової стрілки, і на зовнішню
нескінченну область
проти годинникової стрілки, і на зовнішню
нескінченну область
![]() .
.
Якщо
в області
![]() задана голоморфна функція
задана голоморфна функція
![]() ,
яка неперервна в
,
яка неперервна в
![]() ,
то має місце формула Коші
,
то має місце формула Коші
 (9.78)
(9.78)
Якщо
функція
![]() голоморфна в
голоморфна в
![]() (включаючи нескінченно віддалену точку)
і неперервна в
(включаючи нескінченно віддалену точку)
і неперервна в
![]() ,
то формула Коші має вигляд
,
то формула Коші має вигляд
 (9.79)
(9.79)
-
Перша основна задача для нескінченної площини з еліптичним отвором. Розглянемо нескінченну ізотропну площину з еліптичним отвором, яка перебуває в умовах рівномірного розтягу (стиску) взаємно перпендикулярними напруженнями
 і
і
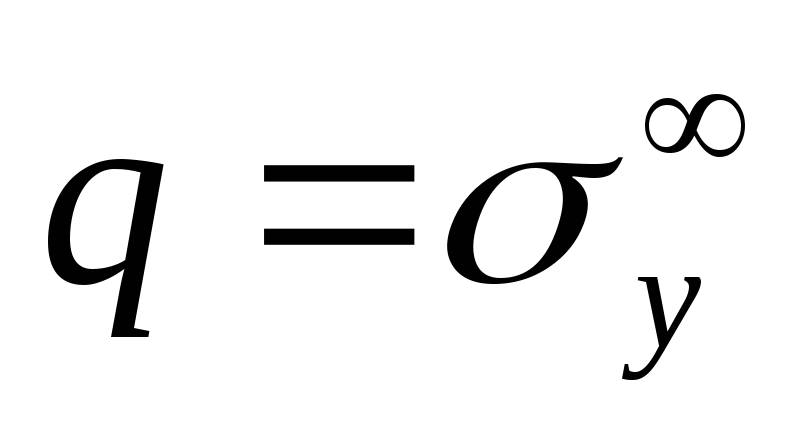 ,
прикладеними “на нескінченності”.
Вважаємо, що напрямки дії напружень
паралельні осям еліпса. Зовнішнє
навантаження на контурі отвору
відсутнє.
,
прикладеними “на нескінченності”.
Вважаємо, що напрямки дії напружень
паралельні осям еліпса. Зовнішнє
навантаження на контурі отвору
відсутнє.
Систему
прямокутних координат
![]() виберемо так, як показано на рис. 9.2.
виберемо так, як показано на рис. 9.2.
Функція
![]()
 (9.80)
(9.80)
при
![]() реалізує конформне відображення площини
з круговим отвором
реалізує конформне відображення площини
з круговим отвором
![]() на розглядувану площину з еліптичним
отвором. Тут
на розглядувану площину з еліптичним
отвором. Тут
![]() ;
;
![]() ,
,
![]() – півосі еліпса;
– півосі еліпса;
![]() – ексцентриситет еліпса. Не порушуючи
загальності, приймаємо
– ексцентриситет еліпса. Не порушуючи
загальності, приймаємо
![]() .
.
При
відсутності зовнішнього навантаження
на контурі
![]() граничні умови (9.70) приймають вигляд
граничні умови (9.70) приймають вигляд
![]() . (9.81)
. (9.81)
Оскільки зовнішнє навантаження на пластинку зрівноважене, то компоненти головного вектора дорівнюють нулю і формули (9.77) запишуться так
![]() ;
;
![]() . (9.82)
. (9.82)
Підставляючи (9.82) в (9.81), одержимо
![]() . (9.83)
. (9.83)
Для еліптичного отвору (9.80)
![]() ;
;
![]() ;
;
![]() ;
;
![]() . (9.84)
. (9.84)
Тому співвідношення (9.83) приймає вигляд
![]()
![]() . (9.85)
. (9.85)
Помножимо
(9.85) на
![]() і проінтегруємо по контуру
і проінтегруємо по контуру
![]()
![]()
![]() . (9.86)
. (9.86)
Функції
![]() ,
,
![]() є граничними значеннями функцій
є граничними значеннями функцій
![]() ,
,
![]() ,
які голоморфні в
,
які голоморфні в
![]() ,
тому на підставі (9.79) маємо при
,
тому на підставі (9.79) маємо при
![]()
![]() ;
;
![]() . (9.87)
. (9.87)
Оскільки
![]() в області
в області
![]() ,
тому функції
,
тому функції
![]() ,
,
![]() ,
,
![]() ,
,
![]() є граничними значеннями функцій
є граничними значеннями функцій
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
які голоморфні в області
,
які голоморфні в області
![]() .
Використовуючи формулу (9.78), одержимо
при
.
Використовуючи формулу (9.78), одержимо
при
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() . (9.88)
. (9.88)
Підставляючи (9.87), (9.88) в (9.85), знаходимо
![]() (9.89)
(9.89)
або з врахуванням (9.82)
![]() . (9.90)
. (9.90)
Для
визначення
![]() перейдемо в (9.85) до спряжених величин
перейдемо в (9.85) до спряжених величин
![]()
![]() . (9.91)
. (9.91)
Враховуючи в (9.91) співвідношення (9.89), одержимо після певних перетворень
![]() . (9.92)
. (9.92)
Помножимо
(9.92) на
![]() і проінтегруємо по контуру
і проінтегруємо по контуру
![]() .
Враховуючи, що
.
Враховуючи, що
![]() при
при
![]() ,
одержимо після обчислення відповідних
інтегралів
,
одержимо після обчислення відповідних
інтегралів
![]() . (9.93)
. (9.93)
На
підставі (9.82) визначаємо функцію
![]()
![]() . (9.94)
. (9.94)
Комплексні потенціали (9.90) і (9.94) повністю визначають розв’язок поставленої задачі. При цьому компоненти тензора напружень визначаються за формулами (9.71).
Якщо
в (9.90), (9.94) покласти
![]() ,
то одержимо розв’язок задачі для
пластинки з круговим отвором. При
,
то одержимо розв’язок задачі для
пластинки з круговим отвором. При
![]() еліпс вироджується у відрізок довжиною
2.
еліпс вироджується у відрізок довжиною
2.
Для
прикладу визначимо компоненти тензора
напружень на контурі отвору для точок
якого
![]() .
.
За формулами (9.71), (9.90)

![]() . (9.95)
. (9.95)
Враховуючи,
що на контурі отвору
![]() і позначення (9.57), із (9.95) знаходимо
і позначення (9.57), із (9.95) знаходимо
![]() . (9.96)
. (9.96)
У
випадку одностороннього розтягу площини
в напрямку осі
![]() (
(![]() ;
;
![]() )
формула (9.96) запишеться у вигляді
)
формула (9.96) запишеться у вигляді
![]() . (9.97)
. (9.97)
Найбільші напруження виникають у вершинах еліпса, які належать великій осі,
![]() . (9.98)
. (9.98)
Якщо
прийняти
![]() ,
то еліптичний отвір вироджується в
круговий, а формула (9.96) співпадає з
відповідною формулою (8.86), яка одержана
іншим способом.
,
то еліптичний отвір вироджується в
круговий, а формула (9.96) співпадає з
відповідною формулою (8.86), яка одержана
іншим способом.
-
Друга гранична задача для нескінченної площини з еліптичним отвором. Розглянемо попередню задачу при допущенні, що в еліптичний отвір пластинки вставлено абсолютно жорсткий диск і по всьому контуру спаяний з нею (рис. 9.3). При відсутності зміщень контуру
 (
( )
гранична умова (9.75) другої основної
задачі приймає вигляд
)
гранична умова (9.75) другої основної
задачі приймає вигляд
![]() (9.99)
(9.99)
або з врахуванням (9.82) запишеться так
![]() . (9.100)
. (9.100)
|
Рис. 9.3 |
![]() .
(9.101)
.
(9.101)
На
підставі (9.82) функція
![]() має вигляд
має вигляд
![]() . (9.102)
. (9.102)
Для
визначення
![]() перейдемо в (9.100) до спряжених величин
перейдемо в (9.100) до спряжених величин
![]() . (9.103)
. (9.103)
Підставляючи в (9.103) вирази (9.84), (9.102), знаходимо після певних перетворень
![]()
![]() . (9.104)
. (9.104)
Поступаючи так, як і з співвідношенням (9.92), одержимо
![]() . (9.105)
. (9.105)
Враховуючи
(9.82), визначаємо комплексний потенціал
![]()
![]() . (9.106)
. (9.106)
Компоненти напруженого стану в довільній точці площини через комплексні потенціали можна визначити за формулами (9.71).
Методом інтегралів типу Коші можна розв’язати ряд інших практично важливих задач плоскої теорії пружності.

