Контрольные вопросы

1. Что называется переходной характеристикой? Импульсной переходной характеристикой?

2. Как получить кривую переходного процесса при сложной форме входного воздействия (меандр либо «лестница»), если известна переходная характеристика звена?

3. Что такое передаточная функция? Как ее получить из дифференциального уравнения системы? Что такое характеристическое уравнение?

4. Как из передаточной функции получить уравнение статического режима работы системы?

5. Приведите уравнение динамики, передаточную функцию, вид переходной характеристики безынерционного звена.

6. Приведите уравнение динамики, передаточную функцию, вид переходной характеристики интегрирующего звена.

7. Приведите уравнение динамики, передаточную функцию, вид переходной характеристики апериодического звена.

8. Приведите уравнение динамики, передаточную функцию, вид переходной характеристики колебательного звена.

9. Приведите уравнение динамики, передаточную функцию, вид переходной характеристики консервативного звена.

10. Почему инерционные звенья второго порядка с коэффициентом затухания большим или равным единице не являются элементарными?

11. Какое звено называется идеальным дифференцирующим? Почему его нельзя реализовать?

12. Приведите уравнение динамики, передаточную функцию, вид переходной характеристики реального дифференцирующего звена.

13. Назовите основные динамические показатели качества. Как они определяются?

3. Глава3. Частотные характеристики типовых динамических звеньев

   1. 3.1. Виды частотных характеристик линейных систем

Частотные характеристики описывают передаточные свойства элементов и АСУ в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Они находят применение в ТАУ, так как реальные возмущения, а, следовательно, и реакции на них элемента или АСУ могут быть представлены как сумма гармонических сигналов. Частотные характеристики широко используются при теоретических и экспериментальных исследованиях систем автоматического регулирования. По ним можно произвести исследование систем на устойчивость, оценить качество переходных процессов и выбрать корректирующие устройства.

Р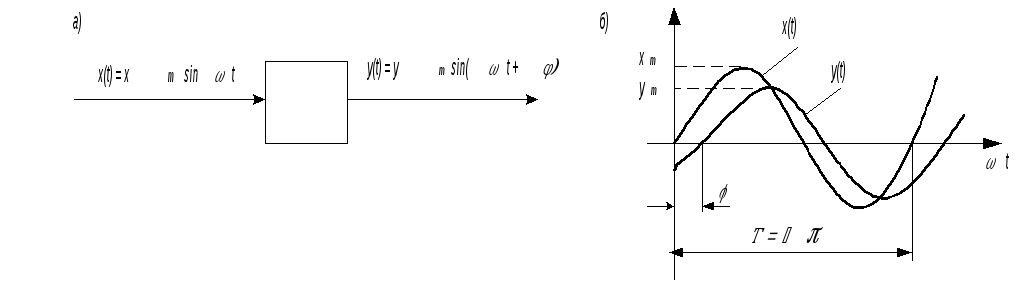

-

ассмотримсущностьиразновидностичастотных характеристик. Пусть на вход линейного элемента (рис. 12 а) в момент времениt = 0 подано гармоническое воздействие с частотой: x(t) = x_m sin t.

Рис. 12. Получение частотных характеристик

По завершении переходного процесса установится режим вынужденных колебаний и выходная величина y(t)будет изменяться по тому же закону, что и входнаяx(t),но в общем случае с другой амплитудойy_mи с фазовым сдвигомпо оси времени относительно входного сигнала (рис. 12б):y(t) = y_m sin(t – ). Проведя аналогичный опыт, но при другой частоте, можно увидеть, что амплитудаy_mи фазовый сдвиг изменились, т. е. они зависят от частоты. Можно также убедиться, что для другого элемента зависимости параметровy_m и от частоты иные. Поэтому такие зависимости могут служить характеристиками динамических свойств элементов.

Разновидности частотных характеристик, наиболее часто используемых в теории управления:

• амплитудно-частотная характеристика (АЧХ);

• фазочастотная характеристика (ФЧХ);

• амплитудно-фазовая частотная характеристика (АФЧХ).

• логарифмические амплитудно-частотная и фазочастотная характеристики (ЛАЧХ и ЛФЧХ).

Для получения частотных характеристик используется, так называемая, частотная передаточная функция, получаемая из передаточной функции путем формальной замены :

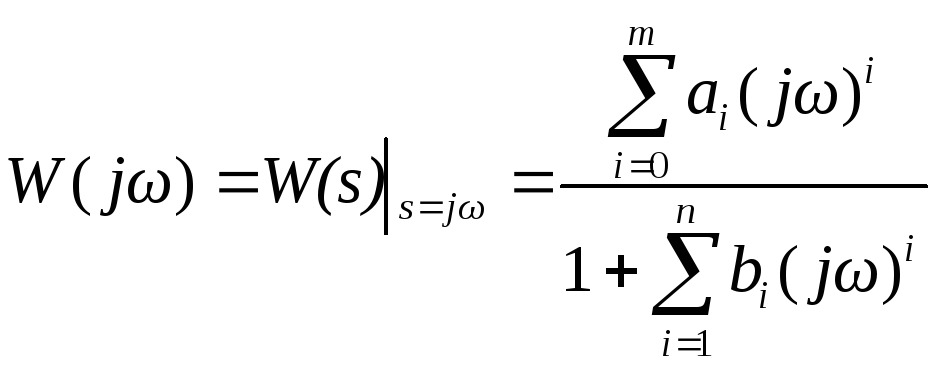, (19)

где ,– коэффициенты полинома, а,– степень полинома числителя и знаменателя передаточной функции.

Выражение (19) можно представить в виде вектора на комплексной плоскости. Проекции вектора на действительную и мнимую оси называют соответственно действительной и мнимой частотными характеристиками и обозначаютP( ), Q( ). Это позволяет записать частотную передаточную функцию в алгебраической форме:

W(j) = P( ) +j Q( ). (20)

Кроме того, частотную передаточную функцию, как и любую комплексную величину, можно представить в тригонометрической и показательной формах:

W(j) = A( )cos () + j A( )sin ()=A()e^j(), (21)

где A()– модуль функции; () – аргумент функции.

Амплитудно-частотная характеристика (АЧХ) – зависимость отношения амплитуд выходного и входного сигналов от частоты:

(22)

АЧХ показывает, как элемент пропускает сигналы различной частоты. Пример АЧХ приведен на рис. 13а. Из уравнений (6), (21) и (22) очевидно, что уравнение АЧХ будет соответствоватьA():

A( ) =  W(j)  = (23)

где P( ) и Q( ) – вещественная и мнимая части частотной ПФ. Для их нахождения необходимо избавиться от мнимости в знаменателе, умножением на сопряженную знаменателю комплексную величину.

Фазочастотная характеристика (ФЧХ) – зависимость фазового сдвига между входным и выходным сигналами от частоты. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах. Пример ФЧХ приведен на рис. 13б. Очевидно, что уравнение ФЧХ будет соответствовать уравнению аргумента()из (21):

 () = arg W(j) = (24)

Физический смысл АЧХ и ФЧХ:

1) АЧХ показывает, как изменяется протекание сигнала различной частоты, при этом оценка пропускания делается по соотношению амплитуд входных и выходных величин;

2) ФЧХ показывает фазовый сдвиг, вносимый системой на различных частотах.

Частота, после которой значение АЧХ уменьшается ниже 0 дБ (коэффициент усиления меньше 1, сигнал ослабляется), называется частотой среза системы .Частота, после которой значение АЧХ падает ниже –3 дБ (коэффициент усиления меньше, чем 0.708), называется полосой пропускания системы.

Рис. 13. Частотные характеристики:

а – амплитудная; б – фазовая; в – амплитудно-фазовая; г – логарифмическая

Максимум АЧХ соответствует частоте, на которой усиление наибольшее. Значение АЧХ при равно усилению при постоянном сигнале, то есть статическому коэффициенту усиления. Это следует и из равенства

. (25)

Для систем с интегрирующими звеньями частотная характеристика стремится к бесконечности при . Это значит, что их выход бесконечно увеличивается при постоянном входном сигнале.

Амплитудную и фазовую характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ). АФЧХ представляет собой функцию комплексного переменногоj,которую можно представить в показательной форме как W(j)=A()e^j(), гдеA()– модуль функции; () – аргумент функции.

Амплитудно-фазовая частотная характеристика представляет собой график частотной передаточной функции, построенный на комплексной плоскости. Каждому фиксированному значению частоты_i соответствует комплексное число, которое на комплексной плоскости можно изобразить вектором, имеющим длинуA(_i )и угол поворота (_i )(рис. 13в). Отрицательные значения (), соответствующие отставанию выходного сигнала от входного, принято отсчитывать по часовой стрелке от положительного направления действительной оси. При изменении частоты от нуля до бесконечности вектор поворачивается вокруг начала координат, при этом одновременно изменяется длина вектора. Кривая, которую при этом опишет конец вектора, и есть АФЧХ. Каждой точке характеристики соответствует определенное значение частоты. Графическое изображение АФЧХ на комплексной плоскости называется годографом Найквиста (рис. 14).

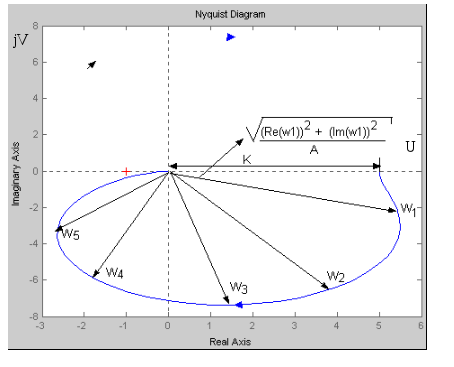
Рис. 14. АФЧХ колебательного звена

АФЧХ можно определить экспериментальным путем, подав на вход звена или системы гармонические колебания и измерив реакцию системы. На выходе системы в установившемся режиме появляются колебания с частотой тестового сигнала, но с измененной амплитудой и фазой. Параметры выходного сигнала (проекции на оси координат или амплитуда и фаза) определяют точку на АФЧХ. Подавая на выход исследуемой системы ряд частот, получим на выходе ряд векторов. Плавно соединяя концы векторов, получим АФЧХ.

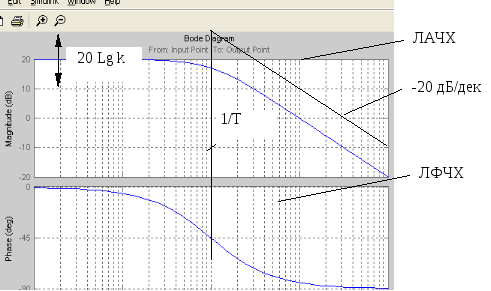
При практических расчетах АСУ (без применения электронных вычислительных машин) удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) – это АЧХ звена, построенная в логарифмических шкалах (lg по оси абсцисс и 20lgA() по оси ординат). Логарифмическая фазочастотная характеристика (ЛФЧХ) имеет логарифмический масштаб только по оси частот. Построение ЛАЧХ типового динамического звена, как правило, сводится к построению асимптотической ЛАЧХ, представляющей собой совокупность отрезков прямых с наклоном, кратным20 дБ\дек. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.

За единицу длины по оси частот логарифмических характеристик принимают декаду.

Декада – интервал частот, заключенный между произвольным значением частоты_iи его десятикратным значением 10_i. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1.

Уравнение ЛАЧХ имеет следующий вид:

L() = 20 lg A( ), (26)

ординаты которой измеряют в логарифмических единицах – беллах(Б) илидецибеллах(дБ).

Если мощность одного сигнала больше (меньше) мощности другого сигнала в 10 раз, то эти мощности отличаются на 1 Б, (lg 10 = 1). Так как мощность гармонического сигнала пропорциональна квадрату его амплитуды, то при применении этой единицы для измерения отношения амплитуд перед логарифмом появляется множитель 2. Например, если на некоторой частоте A( ) = 100, то это означает, что мощности входного и выходного сигналов отличаются в 100² раз, т. е. на 2 lg 100 = 4 Б или на 40 дБ, соответственно, иL() = 20 lg A( ) = 40 дБ.

При построении фазовой частотной характеристики логарифмический масштаб применяют только для оси абсцисс (оси частоты).

На рис. 13 г показаны ЛАЧХL() (толстая линия) и соответствующая ей приближенная (асимптотическая) характеристикаL_а() в виде прямолинейных отрезков (тонкая линия). Частоты, соответствующие точкам стыковки отрезков, называют сопрягающими.Пример ЛАЧХ и ЛФЧХ апериодического звена приведен на рис. 15. Построение ЛАЧХ и ЛФЧХ производится по выражениям:

(27)

По виду частотных характеристик все элементы делятся на две группы:

• минимально-фазовые;

• неминимально-фазовые.

Минимально-фазовый элемент – элемент, у которого все полюсы и нули передаточной функцииW(s)имеют отрицательные действительные части.

Минимально-фазовые элементы дают минимальный фазовый сдвиг ()по сравнению с любыми другими элементами, имеющими такую же амплитудную характеристикуA(), но у которой действительная часть хотя бы одного полюса или нуля положительна.

Минимально-фазовые элементы обладают важным для практических расчетов свойством: их частотная передаточная функция полностью определяется одной из трех составляющих – A( ), P( ) иQ( ). Это существенно упрощает задачи анализа и синтеза минимально-фазовых систем.

Рис. 15. Логарифмические частотные характеристики апериодического звена