3. 6.2. Алгебраический критерий устойчивости Гурвица

При использовании этого критерия необходимо составить из коэффициентов характеристического уравнения (34) определители вида

(35)

где k=1, 2, …, n (n – порядок системы).

Для устойчивости САУ необходимо и достаточно, чтобы все определители имели тот же знак, что и коэффициентb₀. Условие нахождения системы на границе устойчивости –.

Рассмотрим применение критерия Гурвица для характеристического уравнения третьего порядка

Условия устойчивости по Гурвицу будут

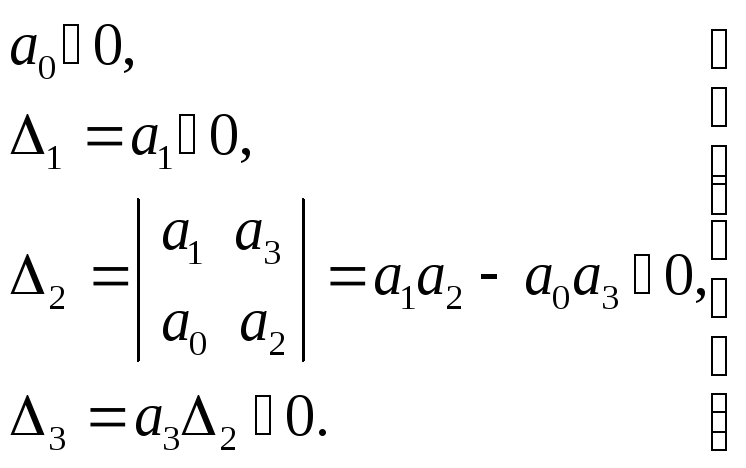
Как правило, в характеристическом уравнении системы коэффициент b₀положителен, поэтому для определения устойчивости необходимо проверить, чтобы все определители были положительны.

4. 6.3. Алгебраический критерий устойчивости Рауса

Для реализации критерия Рауса необходимо заполнить специальную таблицу на основе коэффициентов характеристического уравнения замкнутой системы (табл.13):

1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;

2) во второй строке – с нечетными;

3) остальные элементы таблицы определяется по формуле

, (36)

где ,i3 – номер строки,k– номер столбца.

4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.

Таблица 13

Критерий Рауса

Ri	i\k	1	2	3	4
–	1	C11 = b0	C21 = b2	C31 = b4	...
–	2	C12 = b1	C22 = b3	C32 = b5	...
R3 = C11/C12	3	C13 = C21-R3C22	C23 = C31-R3C32	C33 = C41-R3C42	...
R4 = C12/C13	4	C14 = C22-R4C23	C24 = C32-R4C33	C34 = C42-R4C43	...
...	...	...	...	...	...

Критерий Рауса формулируется следующим образом: для того чтобы САУ была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса C₁₁, C₁₂, C₁₃,... были знакопостоянны (как правило, положительны). Если это не выполняется, то система неустойчива, а количество правых корней равно числу перемен знака в первом столбце.

Рассмотрим пример использования критерия Рауса. Пусть система задается структурной схемой, представленной на рис. 50.

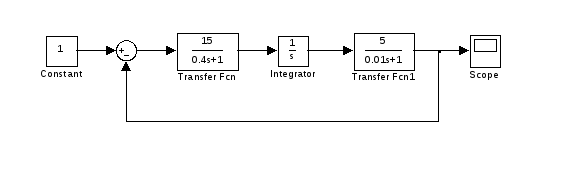
Рис. 50. Структурная схема САУ

Характеристическое уравнение замкнутой системы можно получить из (33):

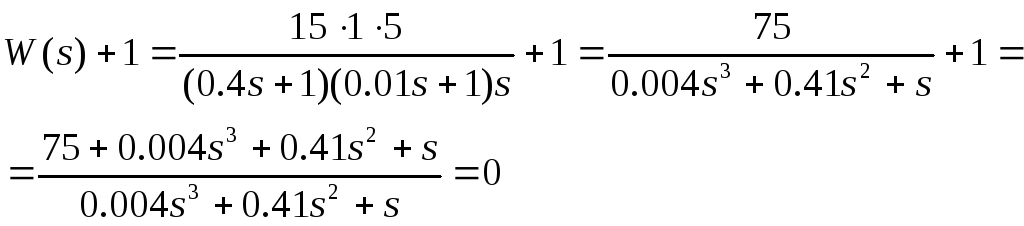
Следовательно, характеристическое уравнение системы получается в виде

b₀=0.004, b₁=0.41, b₂=1,b₃=75.

Реализация критерия Рауса приведена в табл.14. Система устойчива.

Таблица 14

Реализация критерия Рауса

Ri	i/k	1	2	3
–	1	C11=0.004	C21=1	–
–	2	C12=0.41	C22=75	–
R3=0.00976	3	C13=1–0.00976*75=0.2683	–	–

5. 6.4. Критерий устойчивости Михайлова

Критерий формулируется следующим образом. Для того чтобы все корни характеристического уравнения имели отрицательные вещественные части, необходимо, чтобы после подстановки частоты в соответствующий характеристический полиномD(s) полное приращение его фазы при измененииот 0 досоставлялоn/2, гдеn– степень полиномаD(s). При этом характеристический полином опишет в комплексной плоскости кривую – годограф Михайлова. Если переформулировать критерий проще, это означает, что годограф должен последовательно обходитьnквадрантов комплексной плоскости.

Свойства годографа Михайлова:

• Годограф всегда спиралевиден.

• Годограф начинается с точки на оси реальных чисел.

• Поскольку при K(j)0 (в природе и технике нет безынерционных систем), то годограф уходит в бесконечность.

• При четном nгодограф стремится кпараллельно оси реальных чисел; при нечетномnгодограф стремится кпараллельно оси мнимых чисел.

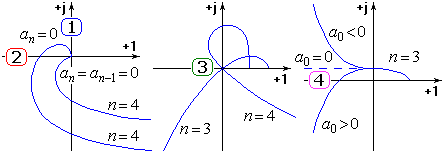
Рис. 51. Определение типа границы устойчивости по виду годографа Михайлова:

1 – астатизм первого порядка – "апериодическая" граница устойчивости; 2 – астатизм второго порядка – "апериодическая" граница устойчивости; 3 –"колебательная" граница устойчивости; 4 – граница устойчивости типа "бесконечный корень"

Рассмотрим пример применения критерия Михайлова. Возьмем систему, структурная схема которой приведена на рис. 50. В MatLabкоманда для построения годографа будет выглядеть следующим образом:

>> sys1=tf([0.004 0.41 1 75],[1])

Transfer function:

0.004 s^3 + 0.41 s^2 + s + 75

>> nyquist(sys1)

Годограф Михайлова приведен на рис. 52. Он последовательно обходит квадранты комплексной плоскости, следовательно, система устойчива.

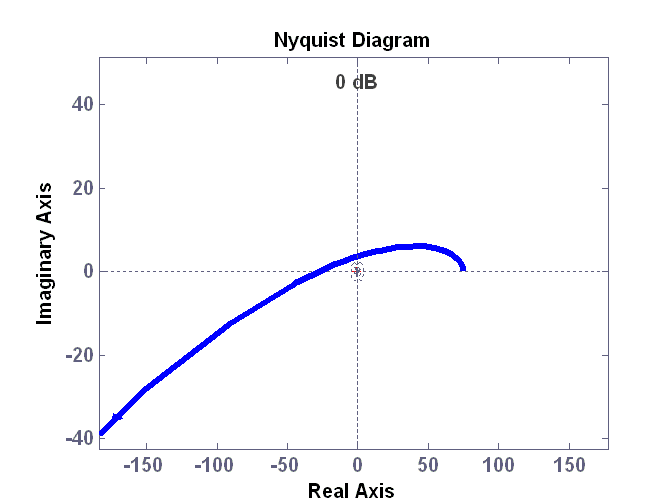
Рис. 52. Годограф Михайлова для системы на рис. 50.