высшая математика

Лекция 24

Предел функции

Даются определения предела функции в точке и односторонних пределов функции, рассматриваются основные свойства пределов функции, бесконечно малых и бесконечно больших функций.

10. Предел функции при x → a. Пусть функция f определена в некоторой окрестности точки х = а за исключением, быть может,

самой точки а. Возьмем последовательность точек {xk } из этой окрестности, сходящуюся к точке а. Значения функции в точках последо-

исключением точки x = 0. Выясним, существует ли предел этой функции в точке х = 0. С этой целью возьмем следующие две последовательности. Пусть первую последовательность составляют числа xk > 0,

Очевидно, последовательность {xk } сходится к точке х = 0, а соответствующая последовательность значений функции будет состоять из единиц и иметь своим пределом число 1.

141

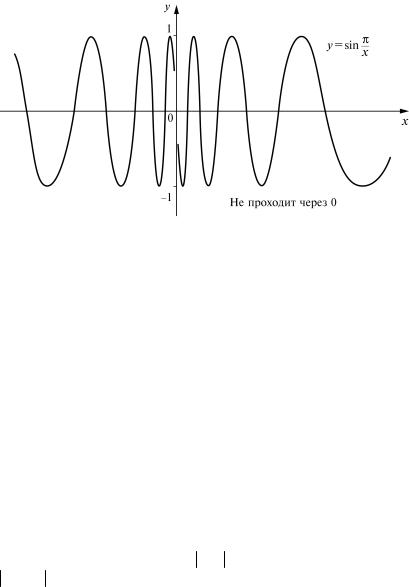
Рис. 1

Теперь возьмем другую последовательность значений аргумента

та {yk } сходится к нулю, и соответствующая последовательность зна-

Таким образом, в первом случае последовательность значений функции сходится к 1, а во втором – к 0. Это означает, что у функции

иллюстрируется на графике этой функции (рис. 1).

Имеет место и другое определение предела функции в точке. Число b называется пределом функции f в точке х = а, если

ε > 0 δ > 0 такое, что x : 0 < x − a < δ выполняется неравенство f (x) − b < ε .

Первое определение основано на понятии пределов последовательностей, и поэтому его называют определением «на языке последовательностей». Второе определение называют определением «на языке ε– δ».

142

Можно доказать, что оба определения равносильны.

Число b называется правым пределом функции в точке х = а, если для любой сходящейся к а последовательности {xn }, члены которой боль-

Естественно, что можно сформулировать эти определения «на языке ε– δ».

Правый и левый пределы функций в точке называются односто-

x → − 0 Следующая теорема устанавливает связь между односторонними пределами и пределом функции.

Теорема 1.

Для того, чтобы функция f имела предел в точке х = a, необходимо и достаточно, чтобы существовали односторонние пределы и они были равны. В этом случае предел функции равен односторонним пределам.

Вводится также определение предела функции и односторонние пределы на бесконечности (или в бесконечно удаленной точке). Число b называется пределом функции f при x → ∞ , если для любой ББП {xn }

соответствующая последовательность значений функции {f (xn )}

143

Теорема 3.

Пусть функции f (x), g (x), h (x) определены в некоторой окрестности точки х = а, кроме, быть может, самой точки а, и удовлетво-

Решение. Здесь можно применить теорему 2:

пределе частного здесь применить нельзя. Однако заметим, что и

144

и, так как при рассмотрении предела функции в точке х = 1 ее аргу-

BD = tg x. Поэтому имеем: sin x < x <tg x. Преобразуем это соотношение:

Рис. 2

145

В силу четности входящих в эти неравенства функций, они спра-

Равенство (2) есть обобщение уже известного предела последовательности.

30. Экономическая интерпретация числа е.

Число е имеет экономическую интерпретацию.

Предположим, что имеем капитал в сумме 1$ и банк «пожертвует» необычно большой процент годовых – 100%. Если проценты будут начисляться один раз в конце года, то величина нашего капитала под конец года будет равна 2$. Обозначим эту величину через V (1), где число в скобках обозначает частоту начисления процентов в год. Если начисление процентов будет осуществляться два раза в год (т.е. каждые полгода по 50%), то будем иметь

Если же начисление процентов будет производиться три раза в год, то

146

Методом математической индукции можно показать, что если проценты начислять n раз в год, то соответствующий капитал составит

В предельном случае, если начисление процентов в течение года

Величина e = 2,7128... может быть интерпретирована как величина, до которой возрастает первоначальный капитал в 1$, когда проценты при степени начисления, равной 100%, будут начисляться непрерывно.

40. Бесконечно малые и бесконечно большие функции.

Функция f (х) называется бесконечно малой (БМФ) в точке х = а, если

ББП (в этом случае иногда пишут lim f (x) = ∞ ).

x→ a

Связь между БМФ и ББФ характеризует следующая теорема.

Теорема 6.

Для того, чтобы функция f в точке х = а (f (x) ≠ 0 при x ≠ a) была

1

БМФ, необходимо и достаточно, чтобы функция f (x) была ББФ.

Связь между пределами функций и БМФ выражается следующей теоремой.

Теорема 7.

Для того, чтобы функция f имела предел в точке х = а, равный b, необходимо и достаточно, чтобы в этой точке функция α (x) = f (x) – b была БМФ.

Свойства БМФ можно описать в следующем виде.

147

Решение. Здесь удобно использовать замену 2x = 1t , чтобы све-

сти этот предел к равенству (2). Действительно, в этом случае имеем,

Решение. Числитель и знаменатель в отдельности при x → ∞ являются ББФ. Поэтому непосредственно перейти к частному пределов на основании теоремы 2 нельзя. Преобразуем функцию, стоящую под знаком предела. Разделим числитель и знаменатель на х в наибольшей степени, т.е. в данном случае, x2. Имеем:

149

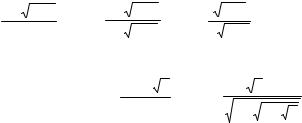
3. Найти пределы:

150