высшая математика

Лекция 16

Квадратичные формы. Классификация кривых второго порядка

Дано определение квадратичной формы, рассмотрена диагонализация матрицы квадратичной формы, проведена классификация кривых второго порядка.

10. Квадратичные формы.

Квадратичной формой в пространстве R n (n переменных x1, x2, ..., xn) называется скалярное произведение вида:

где матрица А – симметрическая.

Напомним, что квадратная матрица А, которую не меняет транс-

Канонической квадратичной формой называется квадратичная форма, содержащая только квадраты переменных:

9 1

20. Квадратичная форма в двумерном пространстве и классификация кривых второго порядка. Рассмотрим квадратичную форму в двумерном пространстве:

= a11x2 + 2a12 xy + a22 y2 .

Каноническая квадратичная форма имеет вид:

Q(x′, y′) = λ 1( x)′2 + λ 2( y)′2 .

Кривые второго порядка – эллиптического, гиперболического и параболического типов задаются квадратичными формами в двумерном пространстве, причем, если:

1. λ 1λ 2 > 0 – эллиптический тип; 2. λ 1λ 2 < 0 – гиперболический тип; 3. λ 1λ 2 = 0 – параболический тип.

Пример 2. Определить тип кривой второго порядка, заданной уравнением: 2x2 + 2xy + 2y2 = 1.

Пример 3. Определить тип кривой второго порядка, заданной уравнением 3xy = 1.

Решение. Квадратичной форме отвечает матрица:

Таким образом, 3xy = 1 – гиперболический тип.

20. Диагонализация матрицы квадратичной формы.

Рассмотрим вначале квадратичную форму в двумерном пространстве и найдем оператор Т, диагонализирующий соответствующую ей матрицу

9 2

Согласно примеру (3) Л.15, собственными векторами диагональной матрицы являются единичные базисные векторы, т.е.

Подобная ситуация имеет место и в случае квадратичной формы в пространстве R n, а именно приведение квадратичной формы к каноническому виду (2) можно осуществить с помощью преобразования

где в (6) Т – матрица, приводящая матрицу А квадратичной формы к

! !

диагональному виду; x, y – векторы размерности n.

Матрица Т устроена следующим образом: ее столбцами служат ортонормированные собственные векторы матрицы А (длина каждого вектора равна единице, все попарные скалярные произведения векторов равны нулю). Матрицы такого типа называют ортогональными.

Отметим также, что в этом случае преобразование Т –1АТ = Λ превращается в преобразование Т TАТ = Λ и отпадает необходимость находить обратную матрицу Т –1.

9 3

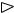Пример 4. Найти ортогональную матрицу, приводящую квадратичную форму

Q(x1, x2, x3) = 6x12 + 3x22 + 3x32 + 4x1 x2 + 4x1 x3 – 8x2 x3

кканоническому виду, и записать канонический вид квадратичной фор-

мы.

Решение. Матрица этой квадратичной формы имеет вид

9 4

Ей соответствует невырожденное линейное преобразование (6) вида:

9 5

применяя которое, получим искомую квадратичную форму

Q(y1, y2,y3) = –2y12 + 7y22 + 7y32.

!Задания для самостоятельной работы

1. Записать матрицу каждой из квадратичных форм:

а) Q (x1, x2, x3, x4) = 4x12 + x32 – 2x42 + x1x2 + 8x1x4 – 10x2x3; б) Q (x1, x2) = x12 – 3x1x2 + 2x22.

2. Записать квадратичную форму по данной матрице А:

4. Найти ортогональное преобразование, приводящее к каноническому виду квадратичную форму Q (x1, x2,..., xn), и записать соответствующий канонический вид квадратичной формы:

а) Q (x1, x2, x3) = x1x2 + x2x3;

б) Q (x1, x2, x3) = x12 + 5x22 – 4x32 + 2x1x2 – 4x1x3.

9 6

Лекция 17

Кривые второго порядка

Изучаются канонические уравнения кривых второго порядка, рассматривается преобразование кривых второго порядка к каноническому виду.

10. Канонические уравнения кривых второго по-

рядка. Общее уравнение кривой второго порядка имеет вид:

липс – геометрическое место точек плоскости, сумма расстояний от которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная (ее обозначают 2а), причем эта постоянная больше расстояния между фокусами. Расстояние между фокусами обозна-

где b2 = a2 – c2, a – большая полуось эллипса, b – малая полуось (рис. 1).

9 7

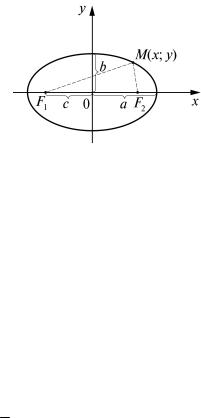
Рис. 1

в) Гипербола. Геометрическое определение: гиперболой называется геометрическое место точек плоскости, абсолютная величина разности от которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная (ее обозначают 2а), причем эта постоянная меньше расстояния между фокусами. Расстояние между фокусами обозначим 2с.

Если за ось Ox принять прямую, проходящую через фокусы F1 и F2, а за ось Oy – перпендикуляр к оси Ox в середине отрезка F1F2, то каноническое (простейшее) уравнение гиперболы примет вид

где b2 = c2 – a2, а – действительная полуось, b – мнимая полуось гиперболы (рис. 2).

Отношение ac = ε > 1 называется эксцентриситетом гиперболы.

Гипербола, у которой a = b, называется равносторонней.

нением гиперболы, но действительной осью этой гиперболы служит отрезок оси Oy длиной 2b.

Отметим, что уравнение (3) действительно уравнение кривой гиперболического типа, т.к., согласно (Л.15.3),

9 8

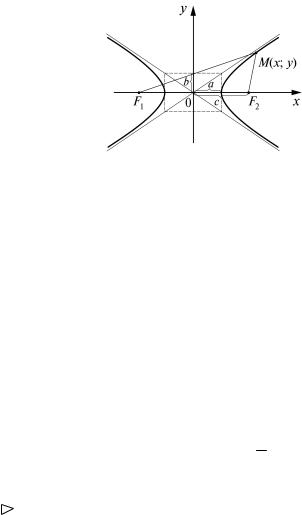
Рис. 2

г) Парабола. Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Каноническое уравнение параболы, симметричной относительно оси Ox и проходящей через начало координат, имеет вид

Когда вершина параболы находится в начале координат и парабола симметрична относительно оси Oy, каноническое уравнение параболы имеет вид x2 = 2py.

В этом случае F (0; p / 2) – фокус, y = − 2p – уравнение директрисы.

20. Преобразование кривых второго порядка к ка-

ноническому виду. Рассмотрим модельный пример.

Пример 1. Найти каноническое уравнение кривой x2 + xy + y2 – 3x – 5y + 5 = 0,

угол ее поворота и построить эту кривую.

Решение. Чтобы избавиться от линейных по х и y слагаемых, совершим преобразование сдвига: x′= x − a, y′= y − b . После подстановки x = x′+ a, y = y′+ b получим

9 9

Рис. 3

(x′+ a)2 + ( x′+ a)( y′+ b) +( y′+ )b 2 − (3 x′+ )a −(5 y′−)b + 5 = 0 . (5)

Приравнивая коэффициенты при x′и y′к нулю, получаем систему уравнений:

100