
высшая математика
.pdf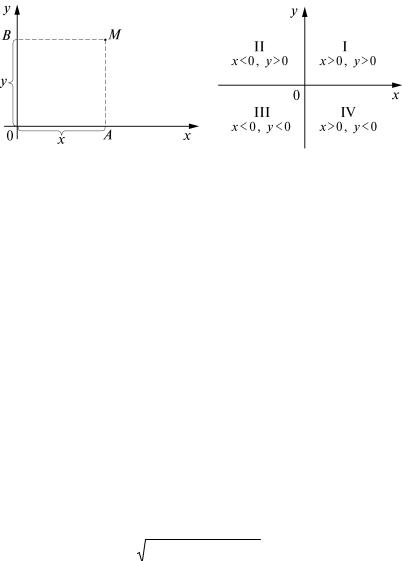
Рис. 3 Рис. 4
наты и, обратно, каждой паре чисел (х; y) соответствует, и при этом только одна точка М на плоскости Oxy такая, что ее абсцисса равна х, а
ордината – y. Значит, прямоугольная система координат на плоскости устанавливает взаимно однозначное соответствие между множеством всех точек плоскости и множеством упорядоченных пар чисел, которое дает возможность при решении геометрических задач применять алгебраические методы.
Оси координат разбивают плоскость на четыре части, их называют четвертями, квадрантами или координатными углами и нумеруют римскими цифрами I, II, III, IV так, как показано на рис. 4. На рис. 4 также указаны знаки координат точек в зависимости от их расположения в той или иной четверти.
Рассмотрим простейшие задачи на применение прямоугольных координат на плоскости.
30. Расстояние между двумя точками.
Теорема 1.
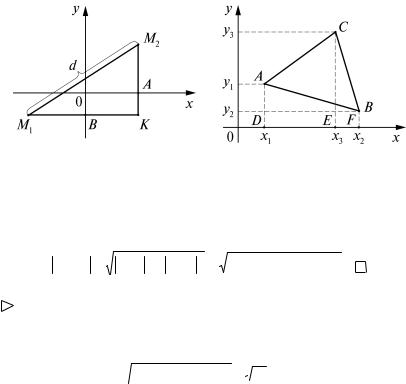
Для любых двух точек M1(x1; y1) и M2(x2; y2) плоскости, расстояние d между ними выражается формулой:
d = (x2 − x1)2 + ( y2 − y1) 2 . |
(2) |
Доказательство. Опустим из точек M2 и M1 перпендикуляры M2A и M1B соответственно на оси Ox и Oy и обозначим через К точку пересечения прямых M2A и M1B (рис. 5).
1 1
|
|
|
|
|
|
|
Рис. 5 |
|
|
|
|
|
|
|
|
|
Рис. 6 |
|
|
|
|
|
|
|
||||||
|
Точка К имеет координаты (х2; у1). Имеем: |
|
M1K |
|
= |
|
x2 − x1 |
|
; |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
M 2 K |
|
= |
|
y2 − |
y1 |
|
. Так как треугольник М М |
К прямоугольный, то по те- |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
ореме Пифагора имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
d = M |
1 |
M |
2 |
|
= M |
K 2 |
+ |
M |
2 |
K 2 = |
(x |
2 |
− |
x )2 + ( y |
2 |
− |
y ) 2 |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
||||||||
Пример 1. Найти расстояние d между точками М1(–1; 2) и
М2(4; 3).
Решение. По формуле (2) находим
d =  (4 − (− 1))2 + (3− 2) 2 =
(4 − (− 1))2 + (3− 2) 2 =  26 .
26 . 
40. Площадь треугольника.
Теорема 2.
Для любых трех точек А(х1; у1), В(х2; у2) и С(х3; у3), не лежащих на одной прямой, площадь S треугольника АВС выражается формулой:
S = |
1 |
|
(x |
2 |
− x |
)( y |
3 |
− y) |
−( |
x |
3 |
− |
x)( |
y |
2 |
− |
)y |
1 |
|
. |
(3) |
|
|
||||||||||||||||||||
|
|
||||||||||||||||||||
|
2 |
|
|
|
1 |
1 |
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Площадь треугольника АВС, изображенного на рис. 6, можно найти так:
SABC = S ADEC + SBCEF − S ABFD , |
(4) |
где SADEC, SBCEF, SABFD – площади соответствующих трапеций. Так как
1 2
SADEC = |
|
|
DE |
|
|
|
AD |
|
+ |
|
|
|
CE |
|
|
= |
|
|
(x3 − x1)( y3 + y1) |
, |
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
SBCEF = |
|
EF |
|
|
|
|
|
|
|
|
EC |
|
|
+ |
|
BF |
|
|
|
|
|
= |
|
(x2 − x3)( y2 + y3) |
|
|
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
SABFD = |
|
|
DF |
|
|
|
|
|
|
AD |
|
+ |
|
|
BF |
|
|
= |
|
(x2 − x1)( y1 + y2) |
|
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
то, подставив выражения для этих площадей в равенство (4), получим
S = |
1 |
|
(x |
− |
x |
2 |
)( |
y + |
y ) +( x |
2 |
− |
x)( |
y |
2 |
+ y) (+ |
|
|
x |
3 |
− )(x y |
3 |
− )y |
|
= |
||||||
|
|
|
|
|||||||||||||||||||||||||||
|
2 |
|
1 |
|
|
1 |
|
2 |
|
|
|
3 |
|
3 |
|
|
|
1 |
1 |
|
|
|||||||||
|
|
|
|
= |
|
1 |
|
(x |
2 |
− x )( |
y |
3 |
− y) −( |
x |
− x)( |
y |
2 |
− |
y) |
|
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
1 |
|
3 |
1 |
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для любого другого расположения треугольника АВС формула (3) доказывается аналогично.
Пример 2. Даны точки А (1;1), В (6;4) и С (8;2). Найти площадь S треугольника АВС.
Решение. По формуле (3)
S = |
1 |
|
|
(6 − 1)( 2 − 1) − ( 8 − )(1 4 − )1 |
|
= |
1 |
|
|
− 16 |
|
= |
8 . |
|
|
|
|
|
|||||||||||
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
50. Деление отрезка в данном отношении.
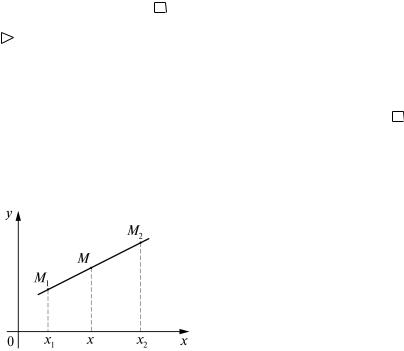
Пусть на плоскости дан произвольный отрезок M1M2 и пусть М – любая точка этого отрезка, отличная от точки M2 (рис. 7).
Определяемое равенством чис-
|
лоλ = |
|
M1 M |
|
|
называется отношени- |
|
|
|
|
|
||
|
|
MM |
|
|
||
|
|
|
||||
|
|
|
2 |
|
|
|
|
ем, в котором точка М делит отре- |
|||||
|
зок М1М2. |
|
|
|
||
|
|
Задача о делении отрезка в дан- |
||||
|
ном отношении состоит в том, что- |
|||||
|
бы по данному отношению λ и дан- |
|||||
|
ным координатам точек М1 и М2 |
|||||
Рис. 7 |
найти координаты точки М. |
|||||
1 3
Решить эту задачу позволяет следующая теорема, которую приведем без доказательства.
Теорема 3.
Если точка М (х; у) делит отрезок М1М2 в отношении λ , то координаты этой точки определяются формулами:
x = |
x1 + |
λ x2 |
; y = |
y1 + |
λ y2 |
, |
(5) |
|
1+ |
λ |
1+ |
λ |
|||||
|
|
|
|
где (х1; у1) – координаты точки М1, (х2; у2) – координаты точки М2.
Следствие. Если M1(x1; y1) и M2(x2; y2) – две произвольные точки и точка М (х; y) – середина отрезка M1M2, т.е. M1M = MM2 , то
λ = 1, и по формулам (5) получаем x = |
x1 + x2 |
, |
y = |
y1 + y2 |
, т.е. каж- |
|
|
||||||
2 |
2 |
|||||
|
|
|
|
дая координата середины отрезка равна полусумме соответствующих координат.
! Упражнения и задания для самостоятельной работы
1. Доказать тождество (1).
2.Доказать теорему 3.
3.Даны точки M1(–2; 3) и M2(5; 4). Найти расстояние d между ними.
4.Даны точки А (0; 1), В (–2; 3) и С (1; 4). Найти площадь S треугольника АВС.
5.Даны точки M1(1; 1) и M2(7; 4). Найти точку М (х; y), которая
вдва раза ближе к M1, чем к M2.
1 4
 Лекция 3
Лекция 3
Полярная система координат. Множества точек на плоскости и их уравнения
Даны определения полярной системы координат и уравнения линии, приведены примеры на нахождение множества точек.
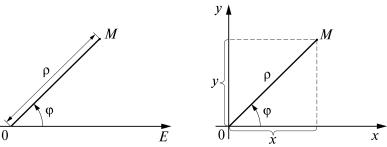
10. Рассмотрим полярную систему координат. Эта система координат состоит из некоторой точки О, называемой полюсом, и исходящего из нее луча ОЕ, называемого полярной осью. Задается также единица масштаба для измерения длин отрезков.
Пусть задана полярная система координат и пусть М – любая точка плоскости. Обозначим через ρ расстояние от точки М до точки О, а через ϕ – угол, на который нужно повернуть против часовой стрелки полярную ось для совмещения с лучом ОМ (рис. 1).
Полярными координатами точки М называются числа ρ и ϕ .
Число ρ считают первой координатой и называют полярным радиу-
сом, |
число ϕ – второй координатой и называют полярным углом. |
M(ρ |
Точка М с полярными координатами ρ и ϕ обозначается так: |
;ϕ ). Обычно считают, что полярные координаты ρ и ϕ изменяются |
|
в пределах: 0 ≤ ρ < +∞ , 0 ≤ ϕ < 2π. |
|
|
Установим связь между полярными координатами точки и ее пря- |
моугольными координатами, считая, что начало прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка М имеет прямоугольные
координаты х и y и полярные координаты ρ и ϕ |
(рис. 2). Имеем: |
х = ρ cos ϕ , y = ρ sin ϕ . |
(1) |
Рис. 1 |
Рис. 2 |
1 5
Формулы (1) выражают прямоугольные координаты через полярные, а выражение полярных координат через прямоугольные следует из формул:
ρ = x2 + y2 , tgϕ = |
y . |
(2) |
|
x |
|
Формула tg ϕ = xy определяет два значения полярного угла ϕ , т.к. ϕ
изменяется в пределах от 0 до 2π . Из этих двух значений угла ϕ выбирают то, при котором удовлетворяются равенства (1).
 Пример 1. Даны прямоугольные координаты точки (2; 2). Найти ее полярные координаты, считая, что полюс совмещен с началом прямоугольной системы координат, а полярная ось совпадает с положительной полуосью абсцисс.
Пример 1. Даны прямоугольные координаты точки (2; 2). Найти ее полярные координаты, считая, что полюс совмещен с началом прямоугольной системы координат, а полярная ось совпадает с положительной полуосью абсцисс.
Решение. По формулам (2) имеем |
ρ = 2 |
2 |
, |
tg ϕ |
= 1. Согласно |
||||||
второму из этих равенств, |
ϕ = |
π |
|
или |
ϕ |
= |
5π |
. |
Но так как |
||
|
|
4 |
|||||||||
|
π |
|
4 |
|
|
|
|
|
|
||
x = 2 > 0 и y = 2 > 0, то ϕ = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|
|
|
|
|
|
|
20. Определение уравнения линии. |
|
|
|
||||||||
Рассмотрим соотношение вида |
|
|
|
|
|
|
|||||
|
F(x, y) = 0, |
|
|
|
|
|
(3) |
||||
связывающее переменные величины х и y. Равенство вида (3) назовем
уравнением с двумя переменными х, y, если это равенство справедли-
во не для всех пар чисел х и y. Примеры уравнений: 3x + 2y = 0, sin x + cos y – 2 = 0.
Если (3) справедливо для всех допустимых пар чисел х и y, то оно называется тождеством. Примеры тождеств:
(x + y) (x – y) – x2 + y2 = 0, (x + y)3 –x3 – 3x2y – 3xy2 – y3 = 0.
Уравнение (3) назовем уравнением множества точек (х; y), если этому уравнению удовлетворяют координаты х и y любой точки множества и не удовлетворяют координаты никакой точки, не принадлежащей этому множеству.
Важным понятием аналитической геометрии является понятие уравнения линии. Пусть на плоскости заданы прямоугольная система координат и некоторая линия L (рис. 3).
Уравнение (3) называется уравнением линии L (в заданной системе координат), если этому уравнению удовлетворяют координаты
1 6
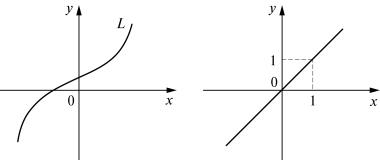
Рис. 3 |
Рис. 4 |
х и y любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Если (3) является уравнением линии L, то говорят, что уравнение (3) определяет или задает линию L.
Линия L может определяться не только уравнением вида (3), но и уравнением вида
F(ρ ,ϕ ) = 0 , |
(4) |
содержащим полярные координаты.
Примеры определения линий уравнениями:
1) х – у = 0. Записав это уравнение в виде у = х, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, представляет собой биссектрисы I и III координатных углов
(рис. 4);
2)х2 – у2 = 0. Запишем уравнение в виде (х – у)(х + у) = 0. Заключаем, что множество точек, координаты которых удовлетворяют этому уравнению, – это две прямые, содержащие биссектрисы четырех координатных углов (рис. 5);
3)х2 + у2 = 0. Множество точек, координаты которых удовлетворяют этому уравнению, состоит из одной точки (0; 0). Здесь уравнение определяет вырожденную линию;
4)х2 + у2 + 2 = 0. Так как при любых х и y числа х2 и у2 неотрицательны, то х2 + у2 + 2 > 0. Нет ни одной точки, координаты которой удовлетворяют данному уравнению, т.е. данное уравнение определяет «пустое» множество точек;
5) ρ = a cos ϕ , где a > 0 – постоянная, переменные ϕ и ρ – поляр-
ные координаты. Обозначим через М точку с полярными координатами (ρ; ϕ ), через А – точку с полярными координатами (а; 0) (рис. 6). Если
1 7

|
Рис. 5 |
|
Рис. 6 |
|
ρ = a cos ϕ |
, где 0 < ϕ < |
π |
, то угол ОМА– прямой, и обратно. Следова- |
|
2 |
||||
|
|
|
||
тельно, множество точек, полярные координаты которых удовлетворя- |
||||
ют данному уравнению, – окружность с диаметром OА (рис. 6); |
||||
6) ρ = |
aϕ , где постоянная a > 0, ρ и ϕ – полярные координаты. Пусть |
|||
М – точка с полярными координатами (ρ ;ϕ ). Если ϕ = 0, то ρ = 0. Таким образом, при увеличении угла ϕ точка M(ρ ; ϕ ), начавшая свое движение в полюсе, движется вокруг него, одновременно удаляясь от полюса. Множество точек, полярные координаты которых удовлетворяют уравнению ϕ = aϕ , называется спиралью Архимеда (рис. 7). При этом предполагается, что ϕ может принимать любые неотрицательные значения.
Если точка М совершает один полный оборот вокруг полюса, то ϕ возрастает на 2π , а ρ – на 2aπ , т.е. спираль рассекает любую прямую, проходящую через полюс, на равные отрезки (не считая отрезка, содержащего полюс), которые имеют длину 2aπ .
Рассмотрим теперь обратную задачу: для заданного какими-то его свойствами множества точек, т.е. для заданной линии L, найти ее уравнение.
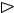 Пример 2. Вывести уравнение (в заданной прямоугольной системе координат) множества точек, каждая из которых отстоит от точки О (0; 0) на расстояние R, т.е. вывести уравнение окружности радиуса R с центром в начале координат (рис. 8).
Пример 2. Вывести уравнение (в заданной прямоугольной системе координат) множества точек, каждая из которых отстоит от точки О (0; 0) на расстояние R, т.е. вывести уравнение окружности радиуса R с центром в начале координат (рис. 8).
Решение. |
Расстояние от произвольной точки М (х; y) до точки |
О вычисляется |
по формуле MO = x 2 + y2 . |
1 8
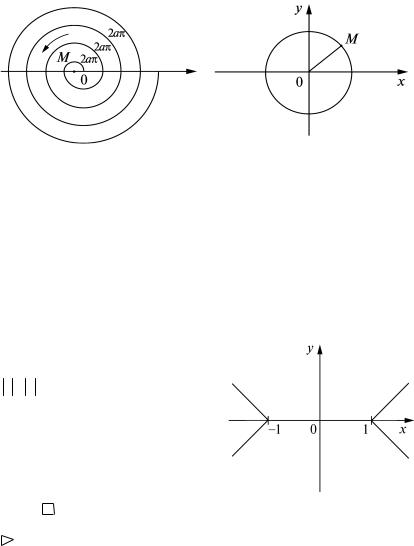
Рис. 7 |
Рис. 8 |
||||
Если точка М лежит на окружности, |
то |
|
MR |
|
= R или |
|
|
||||
MO2 = R2, т.е. координаты точки М удовлетворяют уравнению |
|||||
x2 + y2 = R2. |
(5) |
||||
Уравнение (5) и есть уравнение окружности с центром в начале координат. 
Приведем еще несколько примеров на нахождение множеств точек по уравнениям и неравенствам, связывающим их координаты.
 Пример 3. Найти множество точек (х; y), координаты которых
Пример 3. Найти множество точек (х; y), координаты которых
удовлетворяют уравнению x − y = 1.
Решение. Так как искомое множество точек симметрично относительно координатных осей Oy и Ox, то можно все свести к случаю
x ≥ 0, y ≥ |
0 . Окончательно получа- |
ем множество, изображенное на |
|
рис. 9. |
Рис. 9 |
Пример 4. Показать, что уравнение х2 + 2х + у2 = 0 задает на плоскости некоторую окружность. Найти ее центр и радиус.
Решение. Представим данное уравнение в виде
(х2 + 2х + 1) + у2 = 1 или (x + 1)2 + y2 = 1.
Теперь ясно, что это уравнение окружности с центром в точке С(–1;0) и радиусом 1. 
1 9
! Задания для самостоятельной работы
1. Найти множество точек (х; y), координаты которых удовлетво-
ряют уравнению |
|
x |
|
+ |
|
|
y |
|
= 1. |
|
|
|
|
||||||
2. Установить, |
какое множество точек задает неравенство |
||||||||
x2 + y2 ≤ 4x + 4y . |
|
|
|
||||||
3.На плоскости даны точки А и В. Найти множество точек М, удаленных от А вдвое дальше, чем от В.
4.Установить, при каких значениях параметра а система
|
x 2 + |
y 2 |
= 1, |
|
x + |
y = |
a |
|
не имеет решений, имеет единственное решение, имеет бесчисленное множество решений.
2 0
