∑n |
f (ξ k )∆xk = ∑m |
f (ξ k )∆xk + ∑n |
f (ξ k )∆xk . |
k = 1 |
k = 1 |
k = m+ 1 |
Переходя к пределу в этом равенстве, получим соотношение (5). 
40. Оценки интегралов. Теорема о среднем значении. Теперь рассмотрим некоторые свойства определенных интегралов, описываемые
спомощью неравенств.
1)Если f (x) ≥ 0 на отрезке [a; b], то
b
∫ f (x ) dx ≥ 0 .
a
Доказательство. Действительно, интегральная сумма
σ = |
∑n |
f (ξ k )∆x k для такой функции является неотрицательной, так как |
f (ξ |
)k≥= 10, ∆x |
k |
≥ 0, k = 1, 2, ..., n. Следовательно, предел интегральных сумм |
|
k |
|
|
|
|
|
|
b |
при λ → |
0 , т.е. ∫ f (x ) dx , также будет неотрицательным. |
|
|
|
|
a |
2) Если для f и |
g |
на отрезке [a; b] справедливо неравенство |
f (x) ≤ g(x), то |
|
|
|
b |
b |
|
∫ f (x ) dx ≤ ∫g(x ) dx . |
|
a |
a |
Доказательство. |
Рассмотрим функцию g(x) – f (x). Очевидно, |
x [a; b] : g(x) – f (x) ≥ |
0 |
и в соответствии с предыдущим свойством |
|
b |
|
|
∫(g(x ) − f (x )) dx ≥ 0 . |
|
a |
|
b
Это означает, что ∫(g(x ) − f (x )) dx ≥ 0 . Остается применить свойство
a
3из предыдущего пункта. 
3)Для любой интегрируемой на отрезке [a; b] функции f имеет место неравенство:
b |
|
b |
|
∫ f (x ) dx |
≤ |
∫ |
|
f (x ) |
|
dx . |
(6) |
|
|
a |
|
a |
|
Доказательство. |
|
Действительно, |
|
x [a, b] : − |
|
|
f (x ) |
|
≤ f (x ) ≤ |
|
f (x ) |
|
. |
|
|
|
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
b |
b |
|
− ∫ |
|
f (x ) |
|
dx ≤ ∫ f (x ) dx ≤ ∫ |
|
f (x ) |
|
dx , |
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
a |
|
т.е. справедливо неравенство (6). |
|
|
|
|
|
|
4) Если x |
[a; b] : m ≤ f (x) ≤ M, |
то |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
m(b − |
|
a) ≤ ∫ f (x ) dx ≤ |
M (b − a) . |
(7) |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
Доказательство. Воспользовавшись свойством 2) этого пунк- |
та, имеем: |
|
|
b |
|
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫m dx ≤ ∫ f (x ) dx ≤ ∫M dx |
|
или |
|
|
a |
|
|
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
b |
|
|
b |
|
|
|
|
|
|
m∫dx ≤ ∫ f (x ) dx ≤ M ∫dx . |
|
|
|
|
|
|
a |
|
|
|
a |
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как ∫dx = |
|
|
b − |
a , то получим неравенства (7). |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
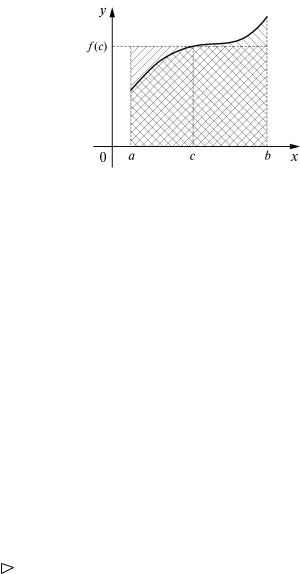
5) Теорема о среднем значении определенного интеграла.
Если функция f непрерывна на отрезке [a; b], то существует точка c [a; b], такая, что
b |
|
∫ f (x ) dx = f (c)(b − a) . |
(8) |
a |
|
Выясним геометрический смысл формулы (8). Если предполо- |
жить, что f (x) ≥ 0 x [a; b], то интеграл слева в (8) |
есть площадь |
криволинейной трапеции, ограниченной графиком функции у = f (x), прямыми х = а, х = b и осью Ox.
В правой части равенства (8) стоит площадь прямоугольника с основанием b – а и высотой f (с), т.е. площадь криволинейной трапеции равна площади некоторого прямоугольника (рис. 2).
Доказательство теоремы. Так как функция f непрерывна на
Рис. 2
отрезке [a; b], то (по второй теореме Вейерштрасса) она достигает своего наименьшего и наибольшего значений (см. Л. 26), т.е. x [a; b]:
|
|
m ≤ f (x) ≤ M, |
где m = min f (x ) , |
M = max f (x ) . |
x [a;b] |
x [a;b] |
|
|
Тогда в соответствии с предыдущим свойством |
|
|
b |
|
|
|
m(b − a) ≤ ∫ f (x ) dx ≤ M (b − a) . |
|
|
a |
|
|
Отсюда имеем |
|
|
|
|
|
1 |
|
b |
|
m ≤ |
|
∫ f (x ) dx ≤ M . |
|
b − |
|
|
|
a a |
Теперь воспользуемся теоремой Больцано – Коши о промежуточном значении непрерывной функции (см. Л.26), получим, что существует точка с [a; b] такая, что
|
1 |
|
b |
f (c) = |
|
∫ f (x ) dx , |
b − |
|
|
a a |
т.е. справедлива формула (8).
Пример 2. Доказать, что функция Дирихлe
0, если x иррационал ьное;
D(x ) =
1, если x рациональн ое,
не интегрируема на любом отрезке [a; b].
Решение. Произведем разбиение отрезка [a; b]: |
|
a = x0 < x1 < x2 < ... < xk-1 < xk < ... < xn = b. |
|
Составим интегральную сумму σ = |
∑n |
D(ξ k )∆x k . |
(9) |
|
|
|
|
k = |
1 |
|
Покажем, |
что |
предел |
интегральных сумм |
(9) при |
λ = max (x k − x k − |
1 ) → |
0 |
не существует. Действительно, если выбрать |
1≤ k ≤ n |
|
|
|
|
|
|
все ξ k иррациональными, то σ = 0, если же выбрать все ξ k |
рациональ- |
ными, то σ = ∑n |
∆x k |
= |
b − a ≠ 0 . |
|
|
|
k = 1 |
|
|
|
|
|
|
Это означает, что не существует числа А, удовлетворяющего определению определенного интеграла. 
!Задания для самостоятельной работы
1.Составить интегральную сумму для функции f (x) = 1 + x на
отрезке [2; 8], деля отрезок на n равных частей и выбирая точки ξ k совпадающими с левыми концами отрезков [xk–1; xk].
Чему равен предел таких интегральных сумм? Сделать то же
самое в случае, когда ξ k = xk , k = 1, 2, ..., n.
|
|
|
|
1 |
2. |
Найти оценки снизу и сверху для интеграла ∫ 4 + x 2 dx . |
|
|
|
|
0 |
3. |
Выяснить, какой из интегралов больше: |
|
1 |
1 |
2 |
2 |
а) ∫ |
1+ x 2 dx или ∫x dx ; |
б) ∫ex 2 dx |
или ∫ex dx . |
|
0 |
0 |
1 |
1 |
2
4. Определить знак интеграла ∫x 3dx .
− 1
Лекция 38
Условия существования определенного интеграла. Нахождение определенного интеграла
Приводятся необходимые, а также достаточные условия интегрируемости функций. Рассматриваются свойства интеграла с переменным верхним пределом, и с его помощью выводится основная формула интегрального исчисления – формула Ньютона-Лейбница. Выводятся формулы замены переменной и интегрирования по частям в определенном интеграле.
10. Необходимое условие интегрируемости функции.
Теорема 1.
Если функция f интегрируема на отрезке [a; b], то она ограничена на [a; b] .
Действительно, предположим, что f неограничена на отрезке [a; b]. Тогда при любом разбиении отрезка [a; b] точками a = = x0 < x1 < ... < xn = b функция будет неограниченной хотя бы на одном
отрезке, например, [xj–1; xj ]. Следовательно, |
можно выбрать точку |
ξ j [xj–1; xj ] и точки ξ k [xk–1; xk ] , k = 1, 2, |
..., j–1, j+1, ..., n |
так, чтобы |
величина f (ξ j)∆ xj , а с ней и вся сумма |
σ = ∑n |
f (ξ k )∆x k , |
были сколь |
|
k = 1 |
|
|
угодно большими. Таким образом, не будет существовать конечного предела интегральных сумм, т.е. функция f не является интегрируемой на отрезке [a; b].
Следовательно, интегрируемая функция ограничена на [a, b]. Теорема 1 доказана. 
Условие ограниченности является необходимым, но не является достаточным. Например, функция Дирихле (пример 2, Л. 37) является ограниченной на любом отрезке, но не является интегрируемой.
20. Достаточные условия интегрируемости.
Справедлива следующая
Теорема 2.
Если функция f непрерывна на отрезке [a; b], то она интегрируема на [a; b] .
Доказательство этой теоремы приводить не будем, так как оно достаточно сложно.
Заметим лишь, что условие непрерывности функции является достаточным условием, но не необходимым.
Можно показать, в частности, что если функция f ограничена на отрезке [a; b] и имеет конечное число точек разрыва, то она также интегрируема на отрезке [a; b]. Интегрируемыми являются и ограниченные монотонные на отрезке [a; b] функции.
Например, функция f (x) = x cos2 x + ex является интегрируемой
на любом отрезке [a; b], |
так как она непрерывна на R. |
Функция |
f (x) = sign x |
(см. Л.23) |
является |
интегрируемой на |
отрезке |
[–1; 1], так |
как только |
в |
точке х = 0 она |
имеет точку |
разрыва |
1-го рода. Функция f (x) = |
1 |
при x |
(0; 1] |
и f (0) = 0 не является |
|
x |
|
|
|
|
|
|
|
|
интегрируемой на отрезке, потому что она не ограничена на [0; 1].
30. Интеграл с переменным верхним пределом. Существование первообразной для непрерывной функ-
ции. Важную роль в интегральном исчислении имеет связь между определенным и неопределенным интегралами. Перейдем к ее исследованию.
Пусть функция f является интегрируемой на отрезке [a; b]. Фиксируем произвольное x [a; b].
Функция f будет интегрируемой на отрезке [a; x], т.е. существует интеграл
x
∫ f (t)dt .
a
Теперь каждому x [a; b] поставим в соответствие число, равное
x
∫ f (t)dt . Это означает, что на отрезке [a; b] будет определена функция
a
x |
|
F(x ) = ∫ f (t)dt . |
(1) |
a
Функция F (x), определенная формулой (1), называется интегралом с переменным верхним пределом. Его основное свойство описывается следующей теоремой.
2 3 6
Теорема 3.
Если функция f непрерывна на отрезке [a; b], то функция F, определяемая формулой (1), является дифференцируемой на [a; b], причем
x |
|
F ′(x ) = (∫ f (t)dt)′ = f (x ) . |
(2) |
a
Иначе говоря, производная от интеграла с переменным верхним пределом равна значению подынтегральной функции в точке, равной верхнему пределу.
Доказательство. Достаточно доказать, что существует
lim |
F(x + |
∆x ) − F(x ) |
= |
f (x ), x [a;b] . |
|
∆x |
∆x → 0 |
|
|
Из определения функции F (x) и свойств интегралов следует:
|
x + ∆x |
x |
x + ∆ x |
|
F (x + ∆x ) = |
∫ f (t)dt = ∫ f (t)dt + |
∫ f (t)dt . |
|
a |
a |
x |
|
Значит, |
|
|
|
|
|
x |
x + ∆ x |
x |
x + ∆x |
F (x + ∆x ) − F (x ) == |
∫ f (t)dt + |
∫ f (t)dt − ∫ f (t)dt = |
∫ f (t)dt . |
|
a |
x |
a |
x |
К полученному интегралу применим теорему о среднем значении. Будем иметь
F (x + ∆ x) – F (x) = f (c)∆ x,
где с – некоторая точка, заключенная между х и x + ∆ x.
Тогда F (x + |
∆x ) − |
F (x ) |
= |
f (c) |
и |
∆x |
|
|
|
|
|
|
|
lim |
F (x + |
∆x ) − |
F (x ) |
= |
lim f (c) = f (x ) , |
|
∆x |
|
∆x → 0 |
|
|
|
|
∆x → 0 |
так как при ∆ x → |
0 имеем c → |
x и функция f непрерывна в точке |
x [a; b]. |
|
|
|
|
|
|
Теорема доказана. |
|
|
|
|
Теорему 3 можно переформулировать следующим образом: если
x
функция f непрерывна на отрезке [a; b], то функция F(x ) = ∫ f (t)dt явля-
a
ется ее первообразной на [a; b]. Следовательно,
2 3 7
∫ f (x ) dx = F(x ) + C .
40. Формула Ньютона-Лейбница. Названная формула счита-
ется основной формулой интегрального исчисления.
Теорема 4.
Если функция f(x) непрерывна на отрезке [a; b] и Ф(х) – какаялибо ее первообразная, то справедлива формула Ньютона-Лейбница
b |
|
∫ f (x ) dx = Φ (b) − Φ (a) . |
(3) |
a
Таким образом, формула (3) сводит вычисление определенного интеграла от непрерывной функции к вычислению разности значений любой ее первообразной на верхнем и нижнем пределах интегрирования.
Доказательство теоремы 4. Пусть Φ (х) – какая-либо перво-
образная для непрерывной функции f на [a; b]. Тогда по теореме 3
x
функция F(x ) = ∫ f (t) dt также является первообразной для f на [a; b].
a
По теореме 1 из Л. 34 две любые первообразные для функции f могут отличаться лишь на постоянную:
F (x) = Φ (x) + C, C – const, x [a; b]. |
(4) |
Положив в (4) |
х = а, получим |
|
|
F (a) = Φ (a) + C. |
|
Но, очевидно, |
F (a) = 0. Значит, C = – Φ (a) . |
|
Поэтому равенство (4) можно записать в виде
x
∫ f (t)dt = Φ (x ) − Φ (a) .
a
Теперь положим здесь х = b и получим формулу Ньютона-Лейб- ница (3). 
Разность Φ (b) – Φ (а) принято обозначать |
Φ (x ) |
|
b |
. Поэтому фор- |
|
|
|
|
a |
|
мулу Ньютона-Лейбница можно записать в виде:
b
∫ f (x ) dx = Φ (x ) ba .
a
Пример 1. Вычислить следующие определенные интегралы:
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) ∫sin 2x dx ; б) ∫xe x 2 dx ; в) ∫ |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
2 |
+ |
2x + |
|
2 |
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
− 1 x |
|
|
|
|
|
|
|
|
Решение. а) Одной из первообразных для функции f (x) = sin 2x |
является функция |
Φ (x) = |
− |
1 |
|
cos 2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому, применяя формулу Ньютона-Лейбница, имеем: |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
π |
1 |
|
|
|
π |
|
|
|
|
|
1 |
|
|
|
а) ∫sin 2x dx = |
− |
|
|
cos 2x |
|
04 |
= − |
(cos |
|
− |
cos 0) = |
; |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 = |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) ∫xe x 2 dx = |
ex 2 |
|
|
(e − 1) |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
dx |
0 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0− 1 = arctg 1− arctg 0 = |
π |
|
в) ∫ |
|
|
= ∫ |
|
|
|
|
|
= |
|
arctg (x + |
|
1) |
. |
|
2 |
+ 2x + 2 |
|
2 |
|
|
|
4 |
|
|
− 1 x |
|
|
− 1 (x |
+ 1) |
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50. |
|
|
Замена |
переменной и интегрирование по час- |
тям в |
определенном |
|
интеграле. |
|
|
|
|
|
|
|
|
Теорема 5.
Пусть функция f(x) непрерывна на отрезке [a; b], а функция x = ϕ (t) имеет непрерывную производную на отрезке [α; β], причем отрезок [a; b] является множеством значений функции x = ϕ (t) и ϕ (α) = a, ϕ (β) = b. Тогда справедлива формула
|
b |
β |
′ |
|
|
∫ f (x ) dx = |
∫ f (ϕ (t))ϕ |
(5) |
|
(t) dt . |
|
a |
α |
|
|
Формула (5) называется формулой замены переменной в определенном интеграле.
Доказательство. Пусть F – первообразная для функции f, т.е.
F ′(x ) = f (x ) , x [a; b].
Тогда имеем:
b |
|
∫ f (x ) dx = F (b) − F (a) . |
(6) |
a
Положим G (t) = F (ϕ (t)). По правилу дифференцирования сложной функции получим, что G′(t) = F ′(ϕ (t)) ϕ ′(t) = f (ϕ (t)) ϕ ′(t) .
Следовательно, функция G (t) есть первообразная для функции f (ϕ (t)) ϕ ′(t) на отрезке [α; β], и по формуле Ньютона-Лейбница найдем:
β
∫ f (ϕ (t))ϕ ′(t) dt = G(β) − G(α) = F(ϕ (β)) − F (ϕ (α)) = F(b) − F (a) . (7)
α Правые части равенств (6) и (7) совпадают. Сравнивая их левые части, получим формулу (5). 
Теорема 6.
Если функции u = u(x) и v = v(x) имеют непрерывные производные на отрезке [a; b], то справедлива формула:
|
|
|
|
|
b |
|
|
|
b |
|
|
|
|
|
|
∫u dv = uv |
|
ab − ∫vdu . |
(8) |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a |
|
Доказательство. Очевидно, функция u(x)v(x) является перво- |
образной для функции |
v(x )u′(x ) + u(x )v′(x ) , |
|
(u(x ) |
v |
′ |
= |
v |
′ |
+ u(x ) |
v′ |
|
(x )) |
|
(x )u (x ) |
|
|
(x ) . Cледовательно, |
|
|
b |
|
|
|
|
|
|
|
|
|
|
ab , |
|
или |
∫(v(x )u′(x ) + u(x )v′(x )) dx = (u(x )v(x )) |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
b |
|
|
∫u(x )v′(x ) dx = (u(x )v(x )) |
|
ab − ∫v(x )u′(x ) dx . |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
Так как u′(x ) dx = |
du , |
v′(x ) dx = dv , то эту формулу можно запи- |
сать в виде (8). 
Формулу (8) называют формулой интегрирования по частям в
определенном интеграле.
|
1 |
x |
|
|
|
|
|
|
Пример 2. Найти интеграл ∫ |
dx . |
|
|
|
|
|
1− x 2 |
|
|
|
|
|
0 |
|
|
|
|
|
|
Решение. Воспользуемся формулой замены переменной. По- |
|
ложим x = sin t, dx = cos t dt. Очевидно, sin 0 = 0, sin |
π |
= 1. Отрезок [0; 1] |
|
2 |
|
|
|
|
|
π |
|
|
является множеством значений функции x = sin t, t |
[0; |
]. По форму- |
|
|
|
|
|
|
|
2 |
|
ле (5) получим:
