высшая математика

Министерство образования Республики Беларусь

УЧРЕЖДЕНИЕОБРАЗОВАНИЯ «ГРОДНЕНСКИЙГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ ЯНКИ КУПАЛЫ» ИНСТИТУТ ПОСЛЕДИПЛОМНОГО ОБРАЗОВАНИЯ

С. А. Минюк, Е. А. Ровба

ВЫСШАЯ МАТЕМАТИКА

Допущено Министерством образования Республики Беларусь

в качестве учебного пособия для студентов экономических специальностей

высших учебных заведений

3-е издание

Гродно 2004

ПРЕДИСЛОВИЕ

Учебное пособие по курсу высшей математики состоит из трех частей: «Линейная алгебра и аналитическая геометрия»; «Введение в анализ. Дифференциальное и интегральное исчисление»; «Функции многих переменных. Дифференциальные и разностные уравнения. Ряды». Эти лекции читались на факультете экономики и управления в Гродненском государственном университете имени Янки Купалы.

Всодержание курса, за исключением, может быть, лекций 10 и 20, вошел традиционный материал, изложенный в учебниках и учебных пособиях по высшей математике. Особенно большое влияние на содержание лекционного материала оказали следующие учебные пособия: В.С.Шипачев «Основы высшей математики» (М., 1969); А. В. Кузнецов

идр. «Сборник задач и упражнений по высшей математике. Общий курс» (Мн., 1994); В.Г.Власов «Конспект лекций по высшей математике» (М.,

1996); Alpha C. Chiang. «Podstawy ekonomiki matematycznej» (Warszawa,

1994). Материал, изложенный в лекциях 10 и 20, в дальнейшем необходим для качественного чтения важного для экономистов курса «Математическое программирование» или аналогичного ему.

Мы старались выработать собственный стиль изложения материала, главным принципом которого является следующий: нематематику нужно больше рассказывать математику, чем доказывать, не потеряв при этом достаточного уровня математической строгости. Преподаватели и студенты знают, насколько «живые» лекции по дисциплине отличаются от учебников по той же дисциплине.

Вначале каждой лекции дается ее краткая аннотация, затем излагается ее содержание с набором типовых практических примеров, в заключение даются задания для самостоятельной работы, выполняя которые обучаемый получает практические навыки решения задач по данной теме. В каждой отдельной лекции используется одинарная нумерация формул, теорем и т.д.; при ссылках используется двойная нумерация, например, выражение «по формуле (Л.15.6)» означает, что эта формула содержится в лекции 15 под номером 6.

Взаключение выражаем глубокую благодарность рецензентам за ряд ценных советов и замечаний.

Втретьем издании устранены технические погрешности второго издания.

3

Часть 1

ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Лекция 1

Предмет математики. Простейшие математические модели в экономике

Данная лекция носит вводный характер: рассмотрены примеры математических моделей простейших экономических ситуаций.

Одной из характерных особенностей математики является ее абстрактность. В связи с этим, каждое отдельно взятое математическое понятие, начиная с простейшего, усваивается нелегко. И несмотря на это, математика доступна самому широкому кругу людей, т.к. простота и доходчивость – это тоже особенность математики. А вот вызвать к математике интерес по возможности у всех учащихся – дело далеко не простое. Мы хотели бы вызвать у Вас не просто интерес, а увлеченность математикой, чтобы она стала для Вас необходимостью, а для людей особо одаренных – целью жизни. Математике человечество обязано многими величайшими открытиями, давшими миру гениев.

Изучение математики развивает логическое мышление, приучает человека к точности, к умению выделять главное, сообщает необходимые сведения для понимания сложных задач, возникающих в различных областях человеческой деятельности.

В связи с возросшей ролью математики в современной науке и технике будущие инженеры, экономисты и научные работники нуждаются в серьезной математической подготовке. Сегодня математика нужна всем. Это веление времени, настоятельная жизненная необходимость. В наше время подтверждается предвидение великого экономиста К. Маркса о том, что наука тогда достигает совершенства, когда начинает пользоваться математикой.

Рассмотрим примеры математических моделей простейших экономических ситуаций.

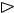Пример 1. Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 680 заготовок типа

4

В. При этом можно применить три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице 1.

Таблица 1

Записать в математической форме условия выполнения задания.

Решение. Обозначим через х1, х2, х3 количество листов материала, раскраиваемых соответственно первым, вторым и третьим способами. Тогда при первом способе раскроя х1 листов будет получено 3х1 заготовок типа А, при втором – 2х2, при третьем – х3. Для полного выполнения задания по заготовкам типа А сумма 3х1 + 2х2 + х3 должна равняться 360, т.е.

ний (1)–(3) выражает в математической форме условия выполнения всего задания по заготовкам А, Б, В.

Пример 2. Три судна доставили в порт 6000 т чугуна, 4000 т железной руды и 3000 т апатитов. Разгрузку можно производить как непосредственно в железнодорожные вагоны для последующей доставки потребителям, так и на портовые склады. В вагоны можно загрузить 8000 т, а остаток груза придется направить на склады. Нужно учесть, что поданные в порт вагоны не приспособлены для перевозки апатитов. Стоимость выгрузки 1 т в вагоны составляет соответственно 4,3; 5,2 и 2,2 денежные единицы, при отправке на склад – 7,8; 6,4 и 3,2 денежные единицы. Записать в математической форме условия полной разгрузки судов, если затраты на нее должны составлять 58 800 денежных единиц.

5

Решение. По условию задачи доставленные в порт чугун, железную руду и апатиты можно разгрузить двумя способами: либо в железнодорожные вагоны, либо в портовые склады. Пусть xij – количество груза в тоннах i-го вида (i = 1,2,3), которые предполагается разгрузить j-ым способом (j = 1,2). Таким образом, задача содержит шесть неизвестных.

Условие полной разгрузки чугуна запишется в виде:

где x11, х12 – части чугуна, разгружаемого соответственно в вагоны и склады.

Аналогичное условие должно выполняться и для железной руды:

Затраты на разгрузку по условию определены в 58800 ден. единиц, что можно выразить так:

Итак, с учетом сложившейся в порту ситуации условия полной разгрузки прибывших судов выражаются в математической форме системой линейных уравнений (4)–(8).

Пример 3. Для строительства домов на 100 строительных площадках выбраны пять типов проектов. По каждому из проектов известны продолжительность закладки фундамента и строительства остальной части дома (таблица 2).

Одновременно можно вести закладку не более 10 фундаментов и строительство не более 15 домов. Записать в математической форме условия, которым должен удовлетворять годовой план (300 рабочих дней) строительства домов при дополнительном требовании, что домов второго типа должно быть построено не менее 10.

Решение. Пусть х1, х2, х3, x4, x5 – количество домов каждого типа, планируемых к строительству в течение года. По условию должно быть построено 100 домов. Этот факт можно выразить так:

6

Таблица 2

Так как одновременно можно вести работы по закладке не более 10 фундаментов, годовой фонд времени по этому виду работ ограничен величиной 3000 рабочих дней. Для реализации плана (х1, х2, х3, x4, x5) только на закладку фундаментов нужно (20х1 + 30х2 + + 35х3 + 30x4 + 40x5) рабочих дней. Это количество не может превышать имеющегося фонда времени, предусмотренного для данного вида работ, значит, должно выполняться неравенство:

Фонд времени на строительство остальной части домов составляет 300·15 = 4500 рабочих дней. На этот вид работ фактически будет потрачено (40х1 + 20х2 + 60х3 + 35x4 + 25x5) рабочих дней. Ясно, что это количество не может превышать имеющийся фонд времени, т.е.

Учитывая последнее требование задачи, придем к неравенству

Остается присоединить естественные условия неотрицательности для остальных переменных:

Таким образом, любой реальный план строительства домов должен удовлетворять смешанной системе, состоящей из линейного уравнения (9) и линейных неравенств (10)–(13).

Пример 4. Фирма решила ежемесячно ассигновать сто тысяч долларов на производство некоторой продукции. Пусть средняя заработная плата по фирме 2000$, а стоимость единицы сырья – 1000$. Требуется определить какое количество рабочих х и какое количество сырья у необходимо приобрести фирме для получения наибольшего объема про-

7

дукции z, если известно, что он им прямо пропорционален с коэффициентом пропорциональности, равным 5.

Математическая модель этой задачи: z = 5xy → max

при условии

2000х + 1000у = 100000

и представляет собой так называемую задачу на условный экстремум.

! Задания для самостоятельной работы

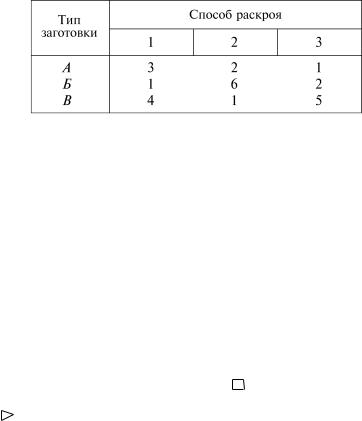
1. Трикотажная фабрика производит свитеры и пуловеры. Все данные приведены в таблице 3.

Таблица 3

Записать в математической форме ограничения, налагаемые на любой реальный план выпуска изделий и состоящие в том, что расход пряжи не превышает ее запаса.

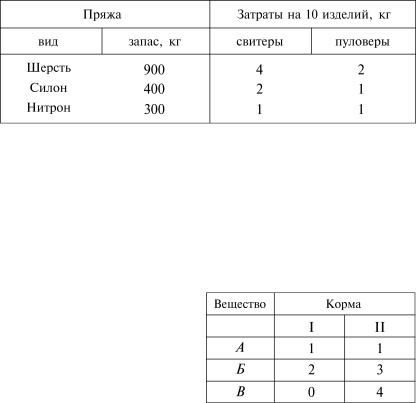
2. В хозяйстве установлено, что откорм животных выгоден лишь тогда, когда они будут получать в суточном рационе не менее 8 ед. питательного вещества А, не менее 14 ед. вещества Б и не менее 3 ед. вещества В, которое содержится в кормах I и II. В таблице 4 указано, сколько единиц каждого вещества содержится в 1 кг корма.

Таблица 4

Записать в математической форме условия, которым должен удовлетворять суточный рацион.

8

Лекция 2

Прямоугольная система координат на плоскости. Простейшие задачи

аналитической геометрии на плоскости

Дано определение декартовой системы координат на плоскости, рассмотрены три простейшие задачи аналитической геометрии на плоскости.

В основе метода координат лежит построение системы координат. Таких систем существует много. Познакомимся с прямоугольной (или декартовой) системой координат.

10. Направленные отрезки и их величины. Одним из основных понятий аналитической геометрии является понятие направленного отрезка. Рассмотрим произвольную прямую. Укажем на ней два взаимно противоположных направления. Выберем одно из них и обозначим его стрелкой (рис. 1). Пусть, кроме того, выбрана единица масштаба для измерения длин отрезков.

Прямая с выбранным на ней направлением называется осью. Рассмотрим на оси две произвольные точки А и В.

Отрезок с граничными точками А и В называется направленным, если указано, какая из точек А и В считается началом, а какая – концом отрезка.

Направленный отрезок с началом в точке А и концом в точке В обозначим AB и будем считать, что он направлен от начала к концу.

В записи AB букву, обозначающую начало отрезка, пишут первой, а букву, обозначающую его конец, – второй.

Длина направленного отрезка AB обозначается так: AB или AB .

Для направленных отрезков, лежащих на оси, введем важное понятие величины направленного отрезка.

Величиной АВ направленного отрезка AB называется вещественное число, равное AB , если направление отрезка и оси совпа-

дают, и равное – AB , если эти направления противоположны.

Отметим, что из определения AB следует, что AB = –BA и AB = BA обозначают одно и то же число. Пусть даны какая-нибудь ось, масштабная

9

единица и точки А, В, С, D, расположенные так, как показано на рис.2. Тогда

AB = AB = 2 , CD = − CD = − 3, BA = − BA = − 2 , DC = DC = 3.

Если точки А и В направленного отрезка AB совпадают, то величина направленного отрезка AB равна нулю, а направление не определено. В дальнейшем направленные отрезки оси будем называть просто отрезками, опуская слово «направленный».

Основное тождество. Для любых трех точек А, В и С на оси

сти. Две взаимно перпендикулярные оси Oх и Оу, имеющие общее начало О и одинаковую единицу масштаба (рис. 3), образуют прямо-

угольную (или декартову) систему координат на плоскости.

Ось Ох называется осью абсцисс, ось Оу – осью ординат. Точка

О пересечения осей называется началом координат. Плоскость, в которой расположены оси Ох и Оу, называется координатной плоскостью и обозначается Оху.

Пусть М – произвольная точка плоскости. Опустим из нее перпендикуляры МА и МВ соответственно на оси Ох и Оу. Прямоугольными координатами х и y точки М будем называть соответственно

величины ОА и ОВ направленных отрезков OA и OB : х = ОА, у = ОВ. Координаты х и y точки М называются соответственно ее абс-

циссой и ординатой.

Тот факт, что точка М имеет координаты х и y, символически обозначают так: М (х; y). При этом первой в скобках указывают абсциссу, а второй – ординату. Начало координат О имеет координаты (0; 0).

Таким образом, при выбранной системе координат каждой точке М плоскости соответствует пара чисел (х; y) – ее прямоугольные коорди-

1 0