высшая математика

Последнее легко получить, если построить вектор

!

col (l; m;n) ,

a =

где l = x2 – x1, m = y2 – y1,

n = z2 – z1.

Пример 1. Уравнение прямой

2x −

y + 3z −

1 =

0,

5x + 4y − z − 7 = 0

записать в канонической форме.

Решение. Исключив

сначала

y,

а

затем

z,

получим:

13x + 11z – 11 = 0 и 17x + 11y – 22 = 0 .

Разрешая каждое из уравнений относительно х, имеем:

x =

11(y − 2)

=

11(z − 1)

, т.е

x

=

y − 2

=

z − 1

.

− 17

− 13

− 11

17

13

Пример 2. Составить уравнение прямой, проходящей через точку

M0 (5; 3; 4)

и параллельной вектору

!

!

!

−

!

a =

2i

+ 5 j

8k .

x − 5

=

y − 3

=

z − 4

.

2

3

−

8

Пример 3. Составить уравнение прямой, проходящей через точку

M

(1; 2; 3)

и

перпендикулярной

векторам

!

!

!

!

и

a =

2i +

3 j +

k

!

0

!

!

!

1

a2

=

3i

+

j

+ 2k .

Решение. Прямая параллельна вектору

!

!

!

!

!

!

i

j

k

!

!

!

2 3 1

=

−

a

= a1

×a2 =

5i

− j

7k .

3

1

2

Поэтому

она определяется уравнением (3),

где l = 5,

m = –1,

n = –7,

x

0

= 1, y

0

= 2, z = 3 и имеет вид

x −

1

=

y −

2

=

z −

3

.

0

5

−

1

−

7

30. Угол между двумя прямыми. Если две прямые зада-

ны

их

каноническими

уравнениями

x −

x1

=

y −

y1

=

z −

z1

и

l1

m1

n1

x −

x2

=

y − y2

=

z −

z2

, то угол между ними определяется по формуле:

l2

m2

n2

cos ϕ

=

l1l2 + m1m2 + n1n2

.

(5)

l 2 + m2 + n2

l 2

+ m2

+ n2

1

1

1

2

2

2

Условие параллельности двух прямых:

l1

=

m1

=

n1

.

(6)

l2

m2

n2

Условие перпендикулярности двух прямых:

l1 l2 + m1 m2 + n1 n2 = 0.

(7)

x2 − x1

y2 − y1 z2 − z1

l1

m1

n1

=

0 .

(8)

l2

m2

n2

Если величины l1, m1, n1 не пропорциональны величинам l2, m2,

n2, то условие (8) является необходимым и достаточным условием

пересечения двух прямых в пространстве.

Пример 4.

В уравнении прямой

x

=

y

=

z

определить пара-

2

−

3

n

метр n так, чтобы эта прямая пересеклась с прямой

x + 1

=

y + 5

=

z

, и

3

2

1

найти точку их пересечения.

Решение. Для нахождения параметра n используем условие (8)

пересечения двух прямых. Здесь

x1 = –1,

y1

= –5,

z1 = 0, x

2 =0,

y2 = 0,

z2 = 0,

l1 = 3,

m1 = 2,

n1 = 1,

l2 = 2,

m2

= –3,

n2 = n. Имеем:

1

5

0

= 0 или 2n + 10 + 3 − 15n =

0

n = 1 .

3

2

1

2

−

3

n

Для

нахождения

координат

точки

пересечения прямых

x

=

y

=

z

и

x +

1

=

y +

5

=

z

выразим из первых уравнений x

и y

2

−

3

1

3

2

1

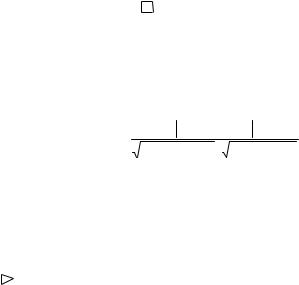
через z : x = 2z,

y = –3z. Подставляя в равенство

x + 1

=

y + 5

, имеем

3

2

2x + 1

=

− 3y + 5

, откуда z = 1. Значит, x = 2, y = –3. Искомая точка пе-

3

2

ресечения

M (2; –3; 1).

прямую, заданную каноническим уравнением (3), и плоскость

Ax + By + Cz + D = 0.

(9)

Тогда угол ϕ между прямой (3) и плоскостью (9) определяется по

формуле:

sin ϕ

=

Al +

Bm +

Cn

.

(10)

A2 + B 2 + C 2

l2 + m2 + n2

Условие параллельности прямой и плоскости:

Al + Bm + Cn = 0.

(11)

Условие перпендикулярности прямой и плоскости:

A

=

B

=

C

.

(12)

l

m

n

Пример 5. Из начала координат опустить перпендикуляр на

прямую

x −

2

=

y −

1

=

z − 3

.

2

3

1

уравнение 2 (2t + 2) + 3 (3t + 1) + t + 3 = 0,

откуда

t =

−

5

. Координа-

7

4

, y = −

8

z =

16

4

8

16

ты точки пересечения

x =

,

,

т.е.

M

; −

;

.

7

7

7

7

7

7

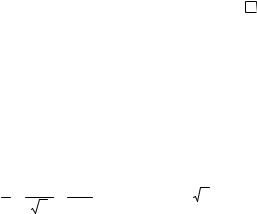
x

=

y

=

z

x

=

y

=

z

или

.

4

8

16

1

− 2

4

−

7

7

7

а) 3x −

2 y +

z − 4 = 0,

б) x + 2 y + z − 4 = 0,

5x +

2y −

3z − 4 = 0;

2x − y + 2z − 3 = 0.

2. Найти угол между прямыми:

x

= y − 2 =

z − 1 и x = t − 2, y = t 2 − 3, z = t .

2

2

2

4. Найти точку пересечения прямой

x − 3

=

y + 1

=

z − 5

и плос-

2

− 1

4

x + 2

=

y

=

z − 5

,

x

=

y − 2

=

z − 1

.

3

2

− 1

3

2

− 1

10. Характеристическое уравнение матрицы.

Линейный оператор (А) задается с помощью квадратной матри-

цы А, под действием которой любой вектор

!

x , принадлежащий про-

странству R n, преобразуется в вектор

!

y , принадлежащий тому же

пространству:

A

!

!

!

R n

!

=

x

y R n , т.е.

Ax

y .

Примером линейного оператора может служить матрица пово-

cos ϕ

sin ϕ

!

!

!

=

!

.

рота (Л.6): R(ϕ ) =

, R( ϕ)

x =

y;

x

y

− sin ϕ

cos ϕ

!

!

(1)

Axi

= λ i xi ,

где λ i – собственное число (значение),

!

xi – собственный вектор.

Из (1) имеем Ax!i − λ i x!i = 0 . Поскольку x!i =

E x!i , то отсюда полу-

чаем A x!i − λ i E x!i = 0 или

!i

= 0 .

′

(A − λ i E)x

(1 )

Условие, при котором система (1/)

имеет нетривиальное решение,

запишется в виде:

det (A − λ E) =

0 .

(2)

1

− 2

1

A =

0

4

− 1 .

0

2

1

1− λ

− 2

1

= 0 (1− λ )[( 4 − λ)( 1− λ) + 2 ]= 0

0

4 − λ

− 1

0

2

1− λ

(1− λ ) (λ 2 − 5λ + 6) = 0 .

a11 − λ

a12

λ

=

0

или λ 2 −

λ (a11 +

a22) +

a11a22 − a12a21 =

0 .

a21

a22 −

По теореме Виета

λ 1λ

2 =

a11a22 −

a12 a21 =

a11

a12

.

(3)

a21

a22

λ 1,2 = a11 + a22 ± (a11 + a22 )2 − 4( a11a22 − a12 a21) =

2

=

a

+ a

22

±

(a

− a

22

)2

+ 4( a

a

)

11

11

12

21 .

2

2

!

= λ

xi

a

− λ

a

xi

=

0

Axi

i

11

i

12

1

.

a21

a22 − λ

i

i

x2

(a

− λ

i

)xi

+

a

xi

=

0, т.к. n − r = 2 − 1 = 1.

11

1

12

2

i

= ca12

a12

x1

!i

=

xi

=

c(λ

−

a

x

c

λ i

− a11

.

i

)

2

11

матрицы

A =

1

1

.

2

0

Решение:

1−

λ

1

=

0

λ 2 −

λ

−

2 =

0

λ 1 =

2, λ 2

= − 1 .

2

− λ

!1

=

a12

=

1

=

1

,

!2

=

a12

=

1

x

c

λ − a

c

2 −

c

x

c

λ

−

a

c

2

.

1

1

2

11

11

Итак,

λ 1 = 2,

λ = − 1,

!1

=

1

,

!2

=

1

x

c

x

c

.

1

2

20.

Приведение

матрицы

к

диагональному

виду. Пусть

λ 1

0

%

0

λ 2

Λ =

0

%

0

(4)

.

% %

% %

0

0

% λ n

Если квадратная матрица Λ

порядка n ×n

имеет собственные

значения λ 1, λ 2, ..., λ S кратности m1, m2, ..., mS

соответственно, причем

∑S

mk = n , то для представления матрицы А в

диагональном виде

k = 1

Λ = Т –1А Т необходимо и достаточно,

чтобы выполнялось условие

rank (A – λ

kE) = n – mk, k = 1, 2,

...,

s.

(5)

Пример 5. Привести матрицу

A =

1

1

к диагональному виду.

2

0

!1

=

1

,

!2

=

1

. Составляем матрицу

T =

1

1

(ее столбцами

x

x

−

2

1

−

2

1

2

1

T − 1 =

3

3

Находим

.

1

−

1

3

3

Убедимся,

что матрица

Т –1А Т

имеет диагональный вид (4).

Действительно,

2

1

4

2

1

1

1

1

1

1

2

0

T

− 1