высшая математика

Лекция 9

Исследование систем линейных уравнений. Метод Гаусса

Сформулирована теорема о совместности систем m линейных уравнений с n неизвестными, рассмотрен метод Гаусса решения и исследования таких систем.

10. Системы линейных уравнений и их исследование.

Рассмотрим систему m линейных уравнений с n неизвестными:

Другие формы записи системы (1):

5 1

решение системы (1) ((2), (3), (4)), если она обращает все ее уравнения в верные равенства.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Система (1) называется однородной, если все свободные члены равны нулю. Операторная форма записи однородной системы имеет вид:

Расширенной матрицей системы (1) называется матрица В, состоящая из матрицы системы, дополненной столбцом свободных членов, т.е.

Теорема Кронекера-Капелли.

Система (1) совместна, если ранг матрицы А (rA) равен рангу матрицы В (rB), и несовместна, если rB > rA.

Пример 1. Исследовать на совместность систему:

Итак, система (7) несовместна.

Пример 2. Исследовать на совместность систему:

5 2

Следствия.

1) Пусть m = n, ∆ = det A ≠ 0 . Тогда rA = rB = n, т.е. система (1) совместна, и ее!решение можно найти методами, изложенными в Л.8.

2) Пусть b = 0 . Тогда rA = rB, т.е. однородная система (5) всегда совместна.

20. Метод Гаусса. Наиболее распространенным точным методом решения систем (1) является метод Гаусса. Суть метода состоит в том, что посредством элементарных преобразований система (1) приводится к треугольному или трапециедальному виду, из которого все решения системы получаются непосредственно.

К элементарным преобразованиям относятся следующие: 1) перестановка любых двух уравнений системы; 2) умножение любого уравнения системы на отличное от нуля число; 3) вычеркивание уравнения, все коэффициенты которого равны нулю; 4) вычитание из любого уравнения системы любого другого, умноженного на отличное от нуля число.

Любое элементарное преобразование приводит к системе вида (1), равносильной данной.

Рассмотрим систему вида (1), где коэффициент a11 ≠ 0 . Если бы

11= 0, то на первое место в системе (1) поставили бы уравнение,

вкотором коэффициент при x1 отличен от нуля. Пусть далее в i-ом

сложим его с i-ым уравнением. В результате получим уравнение

(ai1a11 − a11ai1)x1 + ( ai2a11 − a12ai1) x2 +( a11ai3 − a13ai)1 x3 +

+ ... + (a11ain − a1n ai1)xn = a11bi − b1ai1 ,

где коэффициент при x1 равен нулю.

Преобразуем таким образом все уравнения системы, в которых ai1 ≠ 0 (i = 2,m) и, переобозначая cоответствующие коэффициенты, получим систему

в которой рамкой выделена так называемая остаточная часть системы.

5 3

Преобразование системы (1) в систему (1′) выполнено с помощью ее первого уравнения, называемого разрешающим на данном шаге. Исключалась переменная x1, называемая разрешающей, коэффициент a11 при ней называется разрешающим, столбец коэффициен-

с тем, что в процессе преобразований вычеркиваются уравнения вида

прямым ходом метода Гаусса.

Если в системе (1′) r = n , то она имеет треугольный вид. Из последнего уравнения bnn xn = cn находим xn , из предпоследнего – xn–1 и т.д. и, наконец, из первого – x1 и, тем самым, – единственное решение системы (1). Описанный процесс называют обратным ходом метода Гаусса.

5 4

Совокупность базисных неизвестных назовем базисом системы неизвестных. Общее решение (8) записано относительно базиса (x1, x2, ..., xr). Ясно, что его можно записать относительно и других базисов, которых может быть не более Cnr (число сочетаний из n по r).

Чтобы получить какое-нибудь частное решение системы (1), нужно придать свободным неизвестным некоторые числовые значения. Ясно, что в случае r < n система (1) имеет бесконечное множество решений.

Замечание 1. На практике элементарным преобразованиям подвергают не систему уравнений, а ее расширенную матрицу В. Применительно к матричной записи процедура гауссовских исключений формализуется следующим об-

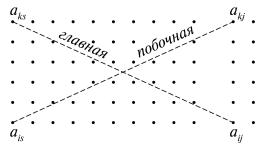
т.д., где разрешающими являются диагональные элементы матрицы. Пересчет элементов матрицы выполняется по следующим правилам: 1) элементы разрешающей строки и всех вышерасположенных строк остаются неизменными; 2) элементы разрешающего столбца, расположенные ниже разрешающего элемента, обращаются в нули; 3) все прочие элементы матрицы вычисляются по правилу прямоугольника, преобразованный элемент равен разности произведений элементов главной и побочной диагоналей

(рис. 1).

Замечание 2. Из метода Гаусса вытекает доказательство теоремы

Кронекера-Капелли. Рис. 1

5 5

Пример 3. Решить систему:

Решение. Последовательно получаем следующие матрицы:

5 6

Лекция 10

Метод полного исключения. Нахождение базисных и опорных решений систем линейных уравнений

Излагается метод полного исключения для решения систем линейных уравнений, приводятся алгоритмы нахождения базисных и опорных решений таких систем.

10. Метод полного исключения. Для решения ряда задач достаточно выполнения операций прямого хода. При решении систем линейных уравнений в Л. 9 выполнялись и прямой, и обратный ходы, в результате которых в расширенной матрице выделялась диагональная подматрица и цель достигалась.

Оказывается, что диагональную подматрицу можно выделить в результате прямого хода, если использовать следующий алгоритм.

Первый шаг. Соответствует исключению неизвестной x1 и выполняется с разрешающим элементом a11 ≠ 0 по правилам прямого хода.

Общий шаг. Соответствует последовательному исключению неизвестных x2, x3,... и выполняется по следующим правилам:

1) назначается разрешающий элемент, им будет коэффициент при исключаемой неизвестной;

2)элементы разрешающей строки остаются неизменными;

3)все элементы разрешающего столбца, кроме разрешающего элемента, заменяются нулями и остаются таковыми до конца преобразований;

4)все прочие элементы матрицы пересчитываются по правилу прямоугольника.

Пример 1. Методом полного исключения решить систему уравнений:

Решение. Используем алгоритм полного исключения и последовательно получаем следующие матрицы:

5 7

По последней матрице записываем общее решение системы уравнений: x1 = 16 + 56 x4 , x2 = 16 − 76 x4 , x3 = 16 + 56 x4 где x4 – любое вещественное число.

20. Нахождение базисных решений системы линейных уравнений. Совместная система линейных алгебраических уравнений называется неопределенной, если она имеет более одного решения. Важную роль в приложениях, в частности, в линейном программировании играют базисные решения такой системы уравнений. Запишем общее решение системы (Л. 9.1) в виде (Л. 9.9):

Базисное решение получается из решения (1), если свободным неизвестным придать нулевые значения, т.е. положить xr+1 = xr+2 = ... = xn = 0. Тогда базисные неизвестные будут равны соот-

ветствующим свободным членам, т.е. x1 = c10, x2 = c20, ..., xr = cr 0. Полученное базисное решение (c10; c20; ..., cr0; 0; ...; 0) соответствует

базису (x1, ..., xr). Если общее решение записать в другом базисе, то получим другое базисное решение. Поскольку из системы n неизвестных можно образовать не более Cnr базисов, то и базисных решений у системы (Л. 9.1) может быть не более Cnr.

Пример 2. Найти все базисные решения системы:

5 8

Решение. В результате прямого хода расширенная матрица данной системы приводится к виду:

которой соответствует система двух уравнений с тремя неизвестными. Так что в общем решении системы две базисные неизвестные линейно выражаются через одну свободную. Возможные свободные неизвестные x1; x2 или x3.

Пусть x1 = 0. Тогда матрица (3) приобретает вид

и, значит, x1 = 14, x3 = 7 , а базисное решение имеет вид (14; 0; 7) .

5 9

30. Нахождение опорных решений. В приложениях,

особенно в математическом программировании, важную роль играют базисные решения, в которых базисные неизвестные принимают неотрицательные значения. Такие решения называют опорными. Чтобы получить опорное решение неопределенной системы линейных уравнений, необходимо с самого начала гауссовых исключений выбирать разрешающие элементы по определенному правилу.

Во-первых, без ограничения общности рассуждений можно считать, что все элементы bi столбца свободных членов исходной расширенной матрицы В системы (Л. 9.1) неотрицательны, ибо если это не так, то обе части соответствующего уравнения нужно умножить на –1.

Опишем правила выбора разрешающих элементов:

1) если в разрешающем столбце есть положительные и отрицательные элементы, то в качестве разрешающего элемента выбирается такой положительный элемент, для которого отношение свободного члена строки к этому элементу будет наименьшим из всех отношений свободных членов к соответствующим положительным элементам разрешающего столбца;

2) если в разрешающем столбце только неположительные элементы, то в качестве разрешающего выбирается такой отрицательный элемент, для которого абсолютная величина отрицательного отношения свободного члена строки к этому элементу будет наибольшей из всех абсолютных величин отрицательных отношений свободных членов к соответствующим отрицательным элементам разрешающего столбца.

Дальше определяем те базисные решения, которые являются и опорными.

6 0