высшая математика

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

! Задания для самостоятельной работы

1. Вычислить определитель

.pdf

Скачиваний:

Добавлен:

18.02.2016

Размер:

5.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 415 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

a11	a12	a13	= a11 a22 a33 + a12 a23 a31 + a13 a21 a32 −
a21	a22	a23	= a11 a22 a33 + a12 a23 a31 + a13 a21 a32 −
a31	a32	a33	(3)

− a11 a23 a32 − a12 a21 a33 − a13 a22 a31 .

Обратим внимание, что каждое слагаемое алгебраической суммы

(3) имеет в качестве множителя один и только один элемент каждой строки и каждого столбца, при этом в сумму в первой части (3) входят все возможные комбинации таких произведений. Аналогичная ситуация наблюдается и для определителя второго порядка.

30. Определитель n-го порядка. Определителем или детерминантом квадратной матрицы порядка n ×n называется скаляр (число), образованный из элементов этой матрицы так:

	a11	a12	…	a1n
	a11	a12	…	a1n
∆ = det A =	a21	a22	…	an2	= ∑n (− 1)1+ j a1j M 1j .	(4)
	…	…	…	…	j = 1
	an1	an2	…	amn

Определитель Mij порядка (n – 1), который получается из матрицы А в результате вычеркивания ее i-ой строки и j-го столбца, называется ми-

нором элемента aij ; i, j = 1, n , а число, равное (− 1)i+ j M ij , – его алгебраическим дополнением.

По формуле (4) определитель порядка n определяется как число, равное сумме произведений элементов первой строки и соответствующих им алгебраических дополнений. Соотношение (4) называют еще формулой разложения определителя по элементам первой строки.

При n = 2 равенство (4) равносильно равенству (1), а при n = 3 оно превращается в формулу (2).

Аналогично находят определитель четвертого порядка: сначала его раскладывают по элементам первой строки и получают в качестве множителей определители третьего порядка, а затем от каждого из полученных этих определителей осуществляют переход к определителям второго порядка, которые вычисляют по формуле (1).

Также для определителя ∆ произвольного порядка n: он выражается сначала через определители M1 j , j = 1, n , порядка n – 1, затем все n

4 1

определителей M1j выражаются через определители (n –2) - го порядка и так далее, до тех пор, пока сумма ∆ будет содержать определители второго порядка, которое легко вычислить по формуле (1).

40. Свойства определителя:

а) определитель n-го порядка сводится к вычислению определителей (n –1)-го порядка посредством его разложения по какой-либо i-ой строке (k-му столбцу):

det A = ∑n	(− 1)i+ k aik M ik =∑ n ( − 1) i+ k aik M ik ;
k = 1	i= 1

б) определитель транспонированной матрицы равен определителю исходной матрицы;

в) если в определителе поменять местами какие-либо две строки или столбца, то определитель изменит знак.

Например,	a11		a12		=	−	a21	a22	;
	a	21	a	22			a	a
		21		22			11	12

г) если какую-либо строку или столбец определителя умножить на число, то такой определитель будет равен исходному, умноженно-

му на это число.
Например,	α a11	α a12	= α	a11	a12	;
Например,	α a11	α a12	= α	a11	a12	;
	a21	a22		a21	a22

д) если все элементы какой-либо строки или столбца определителя равны нулю, то такой определитель равен нулю;

е) если в определителе какие-либо две строки или два столбца равны между собой, то такой определитель равен нулю;

ж) если к элементам какой-либо строки (столбца) определителя прибавить элементы другой строки (столбца) этого же определителя, умноженные на любое число, то определитель не изменяется.

Пример 1. Вычислить определитель:

1	3	4		1	0	0	= (− 1)1+ 1	− 1	1

1	2	5	=	1	− 1	1				= 10 + 5 = 15 .
4	7	6		4	− 5	− 10		− 5	− 10

4 2

з) если каждый элемент некоторой строки представляет собой сумму двух слагаемых, то определитель равен сумме двух определителей, в каждом из которых все строки, кроме упомянутой, такие же, как и в данном определителе, а в упомянутой строке первого определителя стоят первые слагаемые, второго – вторые. Аналогично для столбцов;

и) сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.

Пример 2. Пользуясь свойствами определителей, вычислить:

	sin α	cosα	sin(α + δ)
	sin α	cosα	sin(α + δ)
∆ =	sin β	cosβ	sin(β + δ)	.
	sin λ	cos γ	sin(γ+ δ)	.

Решение. Используя формулу синуса суммы двух углов, имеем:

sin α cosα

∆= sin β cosβ sin λ cos γ

sin α cos δ + sin β cos δ + sin λ cosδ +

cos α sin δ

cosβ sin δ cos γsin δ .

На основании свойства з) определителей можно записать:

sin α cosα

∆= sin β cosβ sin λ cos γ

sin α cosδ sin β cosδ + sin λ cosδ

sin α cosα sin β cosβ sin λ cos γ

cosα sin δ

cosβ sin δ cos γsin δ .

Вследствие пропорциональности первого и третьего столбцов первого определителя и второго и третьего столбцов второго определителя по свойствам г) и е) оба определителя равны нулю. Следовательно, данный определитель равен нулю.

В заключение отметим, что вычисление определителей проводится, как правило, путем последовательного понижения порядка определителя посредством элементарных преобразований, не меняющих его значения.

4 3

− 1

Вычислить определитель

− 1

Пользуясь свойствами определителей, вычислить следующие

определители:

sin2 α

cos2 α

б)

a +

в)

ax +

bx1

sin2

cos2 β

;

b +

;

ay +

by1

sin2

γ 1

cos2 γ

c +

az +

bz1

4. Найти определитель	1	2	3	и все девять алгебраических
4. Найти определитель	2	5	1	и все девять алгебраических
	1	3	4

дополнений его элементов.

5. Решить уравнения: а)

б)

− 1

= 0 ;

= 0 .

4 4

Лекция 8

Действия над матрицами

Рассмотрены простейшие действия над матрицами, вводятся понятия ранга матрицы и обратной матрицы, излагается правило Крамера.

10. Простейшие

действия

над

матрицами.

а)

Сложение матриц.

Результатом сложения двух матриц

и b

порядков (m ×n) является матрица

c , каждый элемент которой пред-

ставляет собой сумму соответствующих элементов матриц

b .

cij =

aij +

bij .

b =

c , где

Отметим, что складываются только матрицы одинаковой раз-

мерности (одного порядка). Например,

не имет

смысла

Свойства сложения:

а1)

А + В = В + А –

переместительное свойство.

а2)

(А + В) + С = А + (В + С)

–

сочетательное свойство.

б) Умножение матрицы на число. Результатом умножения матрицы на число является матрица, каждый элемент которой умножен

							aij .
на это число: λ		a =	c, где cij			= λ	aij .
	Например,		5	6		15	18
	Например,	3		=				.
			− 1			− 3	9
			− 1	3		− 3	9
	в) Умножение матриц. Результатом умножения двух матриц
	размерности (m ×n)			и		размерности (n ×k) является матрица
a	размерности (m ×n)			и	b	размерности (n ×k) является матрица
	размерности m		×k,	каждый элемент которой является резуль-
c	размерности m		×k,	каждый элемент которой является резуль-

татом скалярного перемножения соответствующей строки первой матрицы на соответствующий столбец второй матрицы по формуле (6) Л. 6.

4 5

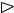
		n
a b =	c ,	где cij = ∑ ail blj .
		l = 1

Подчеркнем, что перемножаются только такие две матрицы, у которых число столбцов первой равно числу строк второй матрицы. На-

0		−	3 4	1		2		11		12
					3	4	=
пример,										.
	1		2 5						32
					5	6				40

Умножение матриц, вообще ным свойством, более того, при мерность матрицы произведения,

говоря, не обладает перестановочперестановке может меняться раз- т.е.

										AB ≠	BA.
Например,
0	0 2		3	=	0		0	2		3	0	0	=	3		0	0		0	≠	3		0
				=				,					=				,			≠
		4	5			2	3		4		1	0			5	0		2	3			5	0	.
1	0	4	5			2	3		4	5	1	0			5	0		2	3			5	0

Единичной матрицей называется такая квадратная матрица, диагональные элементы которой равны единице, а остальные равны нулю.

Отметим, что единичная матрица, а также нулевая матрица обладают перестановочным свойством по отношению к квадратной матрице:

			=
0 a =	a 0, 1 a =	a 1	=	a .

20. Ранг матрицы. Рангом матрицы A (rA= r(A) = rankA) называется наибольший порядок отличного от нуля минора этой матрицы.

При вычислении ранга матрицы производят те же преобразования, что и при вычислении определителя (Л.7).

1		2	3
	4	5	6
Пример 1. Найти ранг матрицы A =				.
	7	8	9

4 6

Р е ш е н и е .

1		2	3	1		4	7	1 4				7	1		4	7	1		4	7
	4	5	6		2	5	8		0	−	3	− 6		0	3	6		0	3	6	,

	7	8	9		3 6		9		0	−	6	− 12		0	3	6		0	0	0

rA = 2.

Квадратная матрица размерности (n n) называется невырожденной, если ее ранг равен n, т.е. определитель этой матрицы отличен от нуля.

Вырожденной квадратной матрицей называется такая матрица, определитель которой равен нулю, т.е. вырожденная квадратная матрица размерности (n n) имеет ранг меньше n.

30. Правило Крамера. Системой n линейных алгебраических уравнений с n неизвестными называют совокупность выражений вида

a11x1	+	a12 x2	+	% +	a1n xn			= b1,
	+	a22 x2	+	% +	a2n xn			= b2	,
a21x1										(1)

%	%	%	% % %		%			%
	+	an2 xn	+	% +	ann xn			= bn ,
an1x1
где aij –коэффициенты системы, причем i, j =							;	x j ,	j =		- неизвес-
						1, n				1, n

тные; bi , i = 1, n – свободные члены.

Систему (1) можно записать в матричной форме:

	a11	a12

a21		a22
	"	"

	an1	an2

или в операторной форме

% a1n

% a2n

% a

A x

(2)

(3)

!			!			a11		…	a1n
	= col(x1	, …		= col( b1, …	, bn) , A =		…	…	…
x			, x n ), b							– матрица сис-
							an1	…
темы (1),									ann

4 7

или в тензорной форме

∑n	aij x j = bi , i =
∑n	aij x j = bi , i =	1, n.
j= 1
			x1
			x2
Совокупность чисел (x1; x2; ...; xn) или			x2	называют решением
Совокупность чисел (x1; x2; ...; xn) или			"	называют решением
			"

			xn

системы (1) ((2) или (3)), если она обращает все уравнения этой системы в верные равенства.

Пусть матрица А невырождена. Тогда для решения системы (1) применяется формула Крамера — универсальная формула решения системы (1):

где ∆ – определитель системы (детерминант матрицы А), ∆ i – дополнительные определители.

Дополнительный определитель ∆ i образуется из определителя

системы заменой i-го столбца на столбец свободных членов.

Пример 2.

Найти (x1;, x2)

если

3x1 −

2x1 +

Решение:

∆ =

− 1

3 +

2 =

∆ 1 =

− 1

1+ 5 = 6,

∆ 2 =

3 1

= 15 − 2 = 13,

∆ 1

, x

2 =

∆ 2

2 5

∆

40. Обратная матрица. Решение системы (2) мето-

дом обратной матрицы. Матрица

A–1

называется обратной к

данной квадратной матрице А, если их произведение равно единичной матрице, т.е.:

						1	0	% 0
						0	1	% 0
AA	− 1	= A	− 1			0	1	% 0
AA		= A		A = 1	= E =				.
					%		% % %
						0	0	% 1
						0	0	% 1

4 8

Отметим, что обратная матрица единственна и существует только для невырожденной квадратной матрицы.

Пример 3.

Выразить решение

системы (2)

через A–1 и b .

Решение.

Имеем:

A− 1 Ax =

A− 1b

1 x =

A− 1b .

Поскольку

то

– операторная форма,

1 x =

A− 1b

xi = ∑n

aij(− 1) bj – тензорная форма.

j = 1

aij(−

1) обратной

Для нахождения элементов

матрицы А–1 исполь-

зуем формулы Крамера (4):

(− 1)i+ j M ji bj

xi =

∆ i

, ∆ i =

∑n (− 1)i+ j M jibj , xi = ∑n

aij(− 1) bj , x1

∆ i

= ∑n

∆

j = 1

∆

(− 1)

(− 1)i + j M ji

(5)

aij

∆

Пример 4.

Найти

–1

если

A =

Решение.

Имеем

М11 = 4, М12 = 3, М21 = 2, М22 = 1.

∆

− 2 .

По формулам (5) получаем:

a11(− 1) =

− 2,

a1( 2− 1)

− 1,

a(2−11) =

a22(− 1)

−

Итак, A

−

− 1 =

1 .

−

Для вычисления обратной матрицы используют также метод Гаусса. Алгоритм вычисления обратной матрицы методом Гаусса состоит в следующем преобразовании:

(A		E) = (E		A− 1) .	(6)

Такое преобразование проводится посредством тех же элементарных действий, что и при вычислении определителей.

Пример 5. Методом Гаусса найти А–1, если	A =	1		2
Пример 5. Методом Гаусса найти А–1, если	A =				.
			3	4
			3	4

4 9

Р е ш е н и е .

1 2	1	0	1	2		1 0	1		0	− 2 1		1 0	− 2		1

													3		1
3 4	0	1	0	− 2	−	3 1	0	−		−		0 1		−		.

									2		3 1		2		2

					−	2		1
Таким образом,			A	− 1 =		3		1 .
							−
						2	−
						2		2
! Задания для самостоятельной работы
1. Определить ранг следующих матриц:
4 3 2			2		3 5			7			0 2			0 0
	0 2 1		1	; б)		1 2		3	; в)			1 0		0 4
a)	0 2 1		1	; б)		1 2		3	; в)			1 0		0 4	.
	0 2 3		3			1 3		5				0 0		3 0
	0 2 3		3			1 3		5				0 0		3 0
2. Найти обратную матрицу А-1 методом Гаусса и проверить,
что АА–1= А–1А=Е :
		1		6	1				1			1	1
	a) A =		2	3	1			A =		2	− 1		2
	a) A =		2	3	1	; б)		A =		2	− 1		2	.
			1	5	2					4		1	3
			1	5	2					4		1	3

3. Пользуясь формулой Крамера, решить следующие системы

уравнений:
4x +		7 y − 13 =	0,		x1 + x2 + 2x3 = − 1,
						− x2	+ 2x3	= − 4,
а)	5x − 3y + 9 = 0;			б)	2x1
						+ x2	+ 4x3	= − 2.
					4x1

4. Методом обратной матрицы решить следующие системы уравнений:

x1 +

x2 +

x3 = 5,

2x1 −

x2 +

x3 =

а)

− x2

+ x3

10, б)

4x2

−

− 16,

2x1

3x1

x2 +

2x3

20;

−

2x2

24.

x1 +

3x1

5 0

<<< < Предыдущая 1 2 3 45 / 415 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.11.2018253.44 Кб9второй курсач(разработка)(Кристина)2.doc
#
13.09.201940.04 Кб6Вуліца Замкавая.docx
#
18.02.2016147.97 Кб2вучэбная праграма 2012.doc
#
19.02.201612.77 Mб65Высшая матем. Учебник.pdf
#
22.09.2019956.93 Кб18Высшая математика (1).doc
#
18.02.20165.88 Mб72высшая математика.pdf
#
18.02.2016192.33 Кб16Вычеты аналитических функций..pdf
#
18.02.2016190.98 Кб4гістарычная навука Бел. раб. праграма 2012.doc
#
14.04.2019380.93 Кб13Гісторыя Беларус(шпоры).doc
#
12.11.2019311.93 Кб3Гісторыя беларускага сялянства. Т.2..docx
#
15.04.2019130.2 Кб4гістрыя вся.docx